|
 |
Hello Guenter,
Well, your macro works! I look forward to see what more you have in mind. At
the current stage, movement is very static I think even for a robot. The
feet also hit each other (or nearly hit?) when they move.
What is your reason for not using ...kinematics? I know nothing about it
I'm afraid.. But Rune has something on his website about this...
http://runevision.com/
Regards,
Hugo
Post a reply to this message
|
 |
|
 |
Guenter wrote:
>
> I've always wanted to do walking insects with accurate leg motion. I didn't
> want to do the kinematics or inverse kinematics so I came up with some
> macro's to create the 2 and 3 segment legs. Attached is my first working
> animation illustrating the these macros.
But that insect would stumble on its own feet.
It looks quite good but the body staying completely constant in its motion
does not look that good. Some simple harmonic motion might much improve
realism.
Christoph
--
POV-Ray tutorials, include files, Sim-POV,
HCR-Edit and more: http://www.tu-bs.de/~y0013390/
Last updated 17 Jun. 2003 _____./\/^>_*_<^\/\.______
Post a reply to this message
|
 |
|
 |
Just thought I'd share my thoughts on leg simulation:
I have tried to do a full inverse kinematic simulation in pov-ray - not
suprisingly, it didn't succeed very well. Professional IK algorithms have
quite complex methods to use up the free degrees of freedom in a 'sensible'
way, which would be quite hard/slow to implement in pov-ray script.
An approximation I thought of is that rarely does the motion of the leg
while it's in the air have to be absolutely accurately controlled. If
vertical movement is ignored, the problem is then reduced to a 2D one. The
next simplification was that for most legs, one degree of movement is only
available at the 'hip' - e.g. in our own legs, sideways movement can only
occur at the hip. A simple rotation of the leg about the hip can therefore
be done to convert it into a 1D problem. An appropriate curve (e.g. a
parabola) of the correct length can be found analytically. See attached for
an example.
The height can then be controlled approximately by just adding a small
amount to the angle of each joint. This works best with many-segmented legs,
so Guenter's method may well be best for his particular application.
-Chris
Post a reply to this message
Attachments:
Download 'ik.gif' (31 KB)
Preview of image 'ik.gif'
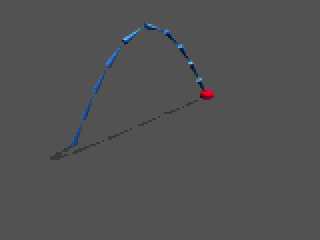
|
 |
|
 |
Hi Chris,
I broke this problem up into two pieces. The first one is a macro that
determines the exact location of the foot for each clock tick. The second
macro determines the locations of the joints. You're right, the exact
location of the foot during a step forward does not need to be very accurite
in height. I just used a sin function. The two segment macro determines
the joint location via a 2D formula. The three segment macro determine the
joint locations by sweeping the angles and trial and error. Using this
method I get two degrees of motion at the hip and 1 degree per joint..
Thanks for the input.
Below is today's version of the first macro that determines the foot
location
// WalkLeg( )
// This takes the inputs, calculates the end of leg position
// with regard to clock and phase. We don't care anything
// about joints here.
//
// Inputs
// clk - clock
// LegStride - how far Foot moves in +x direction
// LegStepHeight - how high Foot moves in +y direction
// LegDownPct - precentage of cycle Foot is down
// LegPhase - what's Foot starting phase, 0-1 == 0-360 degrees
//
// Input/Outputs
// vFoot - Foot postion at clock=0 and phase=0
// returns Foot position after clock and phase adjustments
//
#macro WalkLeg( clk, vFoot, LegStride, LegStepHeight, LegDownPct, LegPhase )
#declare pclk = clk;
#declare pclk = clk + LegPhase/360;
#declare pclk = pclk - int(pclk);
// first we calculate the x position
#switch( pclk )
#range(0,LegDownPct/2) // pushing forward
#declare vFoot = vFoot - < pclk*LegStride, 0,0>;
#break;
#range(LegDownPct/2, 1-LegDownPct/2) // stepping forward
#declare m = LegStride/(1-LegDownPct);
#declare b = -(LegDownPct/2)*LegStride/(1-LegDownPct);
#declare vFoot = vFoot + <m*pclk+b - pclk*LegStride , 0,0>;
#break;
#range(1-LegDownPct/2, 1.0) // pulling forward
#declare vFoot = vFoot + <(1-pclk)*LegStride, 0, 0>;
#break;
#else
#end
// then we calculate the y (height) position
#switch( pclk )
#range(0,LegDownPct/2) // it's down
#break;
#range(LegDownPct/2, 1-LegDownPct/2) // lift during stepping
forward
#declare vFoot = vFoot +
<0,LegStepHeight*sin((pclk-LegDownPct/2)*pi/(1-LegDownPct)), 0>;
#break;
#range(1-LegDownPct/2, 1.0) // it's down again
#break;
#else
#end
#end
Post a reply to this message
|
 |




![]()