 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Added a spherical/Cartesian length function version.
(Midway, right/left)
Looks pretty similar to the stock quilted.
Still throwing darts in the dim light....
Post a reply to this message
Attachments:
Download 'newquiltedpatternandnormal.png' (138 KB)
Preview of image 'newquiltedpatternandnormal.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 10/13/20 1:55 PM, Bald Eagle wrote:
> As for how - those function graphs didn't make themselves, so I'm wondering what
> source information was used and how those graphs were generated for the
> documentation.
> Their existence implies some (non-POV-Ray?) file(s) that were used to graph the
> function, and those might shed some additional light the issue.
indeed... that is likely. all i got when i did the initial load was a
tarball that i still have access to... i looked and that's what we have
for the graphs. i was curious because i thought it /might/ have been
among some of the latex i converted. if you feel inclined to produce a
set of new images, post them here and i'll replace on the wiki
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 10/13/20 4:55 PM, Bald Eagle wrote:
> Added a spherical/Cartesian length function version.
> (Midway, right/left)
>
> Looks pretty similar to the stock quilted.
>
> Still throwing darts in the dim light....
>
I'd guess there isn't much use in translating the non-working normal.cpp
quilted code so below is an my initial attempt at a fix for surfaces
perpendicular to the x, y and z axis. This updated code passes most of
my test cases but of course has varying results with respect to curved
surfaces - as does the original. Whether this is what we want for a
best quilted fix - I don't know! I don't think we really know what the
original coders expected or perhaps even got to one degree or another in
older versions of code
One puzzle for me is I looked at no_bump_scale in the upper right render
(C). I expected it to have some effect on all three surfaces, but it's
only changing the -x one! Not dug into code. Anyone have an idea what's
going on? This touches on me not being a big user of normals. Not sure
I've ever used no_bump_scale myself.
DBL just means double - an sdl float. The normal is the incoming normal.
fabs is abs in sdl. The () ? ... : ... stuff is select. floor and ceil
are floor and ceil. The quilt_cubic you, Bill, understand better than me
at this point.
This the sort of thing you're looking for?
----------
DBL nx = normal.x(), ny = normal.y(), nz = normal.z();
DBL ax = fabs(nx), ay = fabs(ny), az = fabs(nz);
DBL x = EPoint.x(), y = EPoint.y(), z = EPoint.z();
DBL flx = floor(x), fly = floor(y), flz = floor(z);
DBL sx = (x-flx < 0.5) ? -1 : 1,
sy = (y-fly < 0.5) ? -1 : 1,
sz = (z-flz < 0.5) ? -1 : 1;
DBL xm = flx+(ceil(flx+4.4e-8)-flx)/2.0;
DBL ym = fly+(ceil(fly+4.4e-8)-fly)/2.0;
DBL zm = flz+(ceil(flz+4.4e-8)-flz)/2.0;
DBL c0 = pattern->Control0, c1 = pattern->Control1;
DBL na = Tnormal->Amount;
if ((ax >= ay) && (ax >= az))
{
DBL vy = quilt_cubic(fabs(y-ym),c0,c1)*sy;
DBL vz = quilt_cubic(fabs(z-zm),c0,c1)*sz;
nz = (nz < 0.0) ? -1 : 1;
ny = ny + (na * vy);
nz = nz + (na * vz);
}
else if ((ay >= ax) && (ay >= az))
{
DBL vx = quilt_cubic(fabs(x-xm),c0,c1)*sx;
DBL vz = quilt_cubic(fabs(z-zm),c0,c1)*sz;
nx = nx + (na * vx);
ny = (ny < 0.0) ? -1 : 1;
nz = nz + (na * vz);
}
else
{
DBL vx = quilt_cubic(fabs(x-xm),c0,c1)*sx;
DBL vy = quilt_cubic(fabs(y-ym),c0,c1)*sy;
nx = nx + (na * vx);
ny = ny + (na * vy);
nz = (nz < 0.0) ? -1 : 1;
}
normal = Vector3d(nx,ny,nz);
normal.normalize(); // <-- this normal vector what gets updated.
---------
All images in attached image using AA. Why noisy v3.8 results of(A)
looks less noisy at the expense of being quite slow.
A) v3.8 at master.
normal {quilted 0.5 control0 +1.0 control1 +1.0 scale 0.5}
B) povr with a fix.
normal {quilted 0.5 control0 +1.0 control1 +1.0 scale 0.5}
C) normal {quilted 0.5 control0 +1.0 control1 +1.0
no_bump_scale scale 0.5}
D) normal {quilted 0.5 control0 +0.0 control1 +1.0 scale 0.5}
E) normal {quilted 0.5 control0 +1.0 control1 +0.0 scale 0.5}
F) normal {quilted 0.5 control0 +0.0 control1 +0.0 scale 0.5}
G) normal {quilted 0.5 control0 +0.3 control1 +0.3 scale 0.5}
H) normal {quilted 0.5 control0 -0.3 control1 +0.3 scale 0.5}
I) normal {quilted 0.5 control0 +0.3 control1 -0.3 scale 0.5}
Bill P.
Post a reply to this message
Attachments:
Download 'aquiltednormalfix.jpg' (137 KB)
Preview of image 'aquiltednormalfix.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> I'd guess there isn't much use in translating the non-working normal.cpp
> quilted code so
Translating the non-working code would help reproduce the nonworkability.
Then we could see where and why it doesn't work.
> below is an my initial attempt at a fix for surfaces
> perpendicular to the x, y and z axis.
But what did you fix?
> This updated code passes most of
> my test cases but of course has varying results with respect to curved
> surfaces - as does the original. Whether this is what we want for a
> best quilted fix - I don't know! I don't think we really know what the
> original coders expected or perhaps even got to one degree or another in
> older versions of code
I'm not sure what you mean about curved surfaces - no examples have been
provided.
> One puzzle for me is I looked at no_bump_scale in the upper right render
> (C). I expected it to have some effect on all three surfaces, but it's
> only changing the -x one! Not dug into code. Anyone have an idea what's
> going on? This touches on me not being a big user of normals. Not sure
> I've ever used no_bump_scale myself.
You haven't supplied any of your scene code, so I can't tell if you have any
scaling or offsets. The wiki says that no_bump_scale just cancels out any
scaling of the normal depth when the texture or normal itself is scaled.
> DBL just means double - an sdl float. The normal is the incoming normal.
> fabs is abs in sdl. The () ? ... : ... stuff is select. floor and ceil
> are floor and ceil. The quilt_cubic you, Bill, understand better than me
> at this point.
I'll address that and the code supplied below right here.
What I was looking for was as close to a 1:1 translation from the original
source code written in c++ to how it would be done with functions in SDL if it
were written that way from scratch.
Not sure where you are pulling the code below from, but what I had found was:
const DBL INV_SQRT_3_4 = 1.154700538;
DBL quilt_cubic(DBL t, DBL p1, DBL p2)
{
DBL it=(1-t);
DBL itsqrd=it*it;
// DBL itcubed=it*itsqrd;
DBL tsqrd=t*t;
DBL tcubed=t*tsqrd;
DBL val;
// Originally coded as...
// val= (DBL)(itcubed*n1+(tcubed)*n2+3*t*(itsqrd)*p1+3*(tsqrd)*(it)*p2);
//re-written by CEY to optimise because n1=0 n2=1 always.
val = (tcubed + 3.0*t*itsqrd*p1 + 3.0*tsqrd*it*p2) * INV_SQRT_3_4;
return(val);
}
And so my first attempt at translating that was:
#declare INV_SQRT_3_4 = 1.154700538;
#declare Floor = function (T) {select (T, floor (1-T), floor (T))}
#declare IT = function (T) {1-T}
#declare ITsqr = function (T) {pow(IT (T), 2)}
#declare Tsqr = function (T) {pow(T, 2)}
#declare Tcub = function (T) {pow(T, 3)}
#declare Val0 = function (T, _P1, _P2) {
(
pow(T, 3) +
(3 * T * pow(1-T, 2) * _P1) +
(3 * pow(T,2) * (T - pow(T, 2)) * _P2)
)
* INV_SQRT_3_4
}
So:
I would say that if we could get that working as a pigment {function{}}
statement and as a normal{function{}}, then we should be able to then graph it
out the way I did mine to emulate the graphs in the documentation.
They _should_ match (aside from any misleading typos in the docs)
As for the underlying problems with the raytraced result of the pattern, I can
only speculate:
1. it's a function gradient problem since the function may be discontinuous,
have cusps, or whatever else resulting from the use of floor(), etc - since it's
a function designed to be constrained to a unit cube.
I'll have to look at what the isosurface looks like, etc.
2. There's some interface problem between the output of the function and the
rest of what happens to that information after it gets evaluated and sent down
the ray / surface rendering pipeline.
As for the normal-specific function, I'd just need a very basic and specific
explanation of exactly how a given surface normal gets perturbed, in general (by
any user-written scalar function{}), and specifically by this function.
Just so it's crystal clear to me - because what direction does a +y normal get
tilted to? It has 360 degrees of directions to get perturbed in.
I'd also need the following three statements in c++ syntax decrypted, so I could
try translating those into SDL.
const QuiltedPattern *pattern =
dynamic_cast<QuiltedPattern*>(Tnormal->pattern.get());
POV_PATTERN_ASSERT(pattern);
and
normal += (DBL)Tnormal->Amount * value;
> This the sort of thing you're looking for?
>
> ----------
> DBL nx = normal.x(), ny = normal.y(), nz = normal.z();
> DBL ax = fabs(nx), ay = fabs(ny), az = fabs(nz);
>
> DBL x = EPoint.x(), y = EPoint.y(), z = EPoint.z();
> DBL flx = floor(x), fly = floor(y), flz = floor(z);
> DBL sx = (x-flx < 0.5) ? -1 : 1,
> sy = (y-fly < 0.5) ? -1 : 1,
> sz = (z-flz < 0.5) ? -1 : 1;
> DBL xm = flx+(ceil(flx+4.4e-8)-flx)/2.0;
> DBL ym = fly+(ceil(fly+4.4e-8)-fly)/2.0;
> DBL zm = flz+(ceil(flz+4.4e-8)-flz)/2.0;
>
> DBL c0 = pattern->Control0, c1 = pattern->Control1;
> DBL na = Tnormal->Amount;
>
> if ((ax >= ay) && (ax >= az))
> {
> DBL vy = quilt_cubic(fabs(y-ym),c0,c1)*sy;
> DBL vz = quilt_cubic(fabs(z-zm),c0,c1)*sz;
> nz = (nz < 0.0) ? -1 : 1;
> ny = ny + (na * vy);
> nz = nz + (na * vz);
> }
> else if ((ay >= ax) && (ay >= az))
> {
> DBL vx = quilt_cubic(fabs(x-xm),c0,c1)*sx;
> DBL vz = quilt_cubic(fabs(z-zm),c0,c1)*sz;
> nx = nx + (na * vx);
> ny = (ny < 0.0) ? -1 : 1;
> nz = nz + (na * vz);
> }
> else
> {
> DBL vx = quilt_cubic(fabs(x-xm),c0,c1)*sx;
> DBL vy = quilt_cubic(fabs(y-ym),c0,c1)*sy;
> nx = nx + (na * vx);
> ny = ny + (na * vy);
> nz = (nz < 0.0) ? -1 : 1;
> }
> normal = Vector3d(nx,ny,nz);
> normal.normalize(); // <-- this normal vector what gets updated.
> C) normal {quilted 0.5 control0 +1.0 control1 +1.0
> no_bump_scale scale 0.5}
So, as I currently understand it, if the default bump_size is 1.0, then
no_bump_scale decouples the bump_size from the scale 0.5 statement, so that the
area of the normal gets scaled, but the bump_size stays the same at 1.0 instead
of getting shrunk to 0.5 . org> wrote:
> I'd guess there isn't much use in translating the non-working normal.cpp
> quilted code so
Translating the non-working code would help reproduce the nonworkability.
Then we could see where and why it doesn't work.
> below is an my initial attempt at a fix for surfaces
> perpendicular to the x, y and z axis.
But what did you fix?
> This updated code passes most of
> my test cases but of course has varying results with respect to curved
> surfaces - as does the original. Whether this is what we want for a
> best quilted fix - I don't know! I don't think we really know what the
> original coders expected or perhaps even got to one degree or another in
> older versions of code
I'm not sure what you mean about curved surfaces - no examples have been
provided.
> One puzzle for me is I looked at no_bump_scale in the upper right render
> (C). I expected it to have some effect on all three surfaces, but it's
> only changing the -x one! Not dug into code. Anyone have an idea what's
> going on? This touches on me not being a big user of normals. Not sure
> I've ever used no_bump_scale myself.
You haven't supplied any of your scene code, so I can't tell if you have any
scaling or offsets. The wiki says that no_bump_scale just cancels out any
scaling of the normal depth when the texture or normal itself is scaled.
> DBL just means double - an sdl float. The normal is the incoming normal.
> fabs is abs in sdl. The () ? ... : ... stuff is select. floor and ceil
> are floor and ceil. The quilt_cubic you, Bill, understand better than me
> at this point.
I'll address that and the code supplied below right here.
What I was looking for was as close to a 1:1 translation from the original
source code written in c++ to how it would be done with functions in SDL if it
were written that way from scratch.
Not sure where you are pulling the code below from, but what I had found was:
const DBL INV_SQRT_3_4 = 1.154700538;
DBL quilt_cubic(DBL t, DBL p1, DBL p2)
{
DBL it=(1-t);
DBL itsqrd=it*it;
// DBL itcubed=it*itsqrd;
DBL tsqrd=t*t;
DBL tcubed=t*tsqrd;
DBL val;
// Originally coded as...
// val= (DBL)(itcubed*n1+(tcubed)*n2+3*t*(itsqrd)*p1+3*(tsqrd)*(it)*p2);
//re-written by CEY to optimise because n1=0 n2=1 always.
val = (tcubed + 3.0*t*itsqrd*p1 + 3.0*tsqrd*it*p2) * INV_SQRT_3_4;
return(val);
}
And so my first attempt at translating that was:
#declare INV_SQRT_3_4 = 1.154700538;
#declare Floor = function (T) {select (T, floor (1-T), floor (T))}
#declare IT = function (T) {1-T}
#declare ITsqr = function (T) {pow(IT (T), 2)}
#declare Tsqr = function (T) {pow(T, 2)}
#declare Tcub = function (T) {pow(T, 3)}
#declare Val0 = function (T, _P1, _P2) {
(
pow(T, 3) +
(3 * T * pow(1-T, 2) * _P1) +
(3 * pow(T,2) * (T - pow(T, 2)) * _P2)
)
* INV_SQRT_3_4
}
So:
I would say that if we could get that working as a pigment {function{}}
statement and as a normal{function{}}, then we should be able to then graph it
out the way I did mine to emulate the graphs in the documentation.
They _should_ match (aside from any misleading typos in the docs)
As for the underlying problems with the raytraced result of the pattern, I can
only speculate:
1. it's a function gradient problem since the function may be discontinuous,
have cusps, or whatever else resulting from the use of floor(), etc - since it's
a function designed to be constrained to a unit cube.
I'll have to look at what the isosurface looks like, etc.
2. There's some interface problem between the output of the function and the
rest of what happens to that information after it gets evaluated and sent down
the ray / surface rendering pipeline.
As for the normal-specific function, I'd just need a very basic and specific
explanation of exactly how a given surface normal gets perturbed, in general (by
any user-written scalar function{}), and specifically by this function.
Just so it's crystal clear to me - because what direction does a +y normal get
tilted to? It has 360 degrees of directions to get perturbed in.
I'd also need the following three statements in c++ syntax decrypted, so I could
try translating those into SDL.
const QuiltedPattern *pattern =
dynamic_cast<QuiltedPattern*>(Tnormal->pattern.get());
POV_PATTERN_ASSERT(pattern);
and
normal += (DBL)Tnormal->Amount * value;
> This the sort of thing you're looking for?
>
> ----------
> DBL nx = normal.x(), ny = normal.y(), nz = normal.z();
> DBL ax = fabs(nx), ay = fabs(ny), az = fabs(nz);
>
> DBL x = EPoint.x(), y = EPoint.y(), z = EPoint.z();
> DBL flx = floor(x), fly = floor(y), flz = floor(z);
> DBL sx = (x-flx < 0.5) ? -1 : 1,
> sy = (y-fly < 0.5) ? -1 : 1,
> sz = (z-flz < 0.5) ? -1 : 1;
> DBL xm = flx+(ceil(flx+4.4e-8)-flx)/2.0;
> DBL ym = fly+(ceil(fly+4.4e-8)-fly)/2.0;
> DBL zm = flz+(ceil(flz+4.4e-8)-flz)/2.0;
>
> DBL c0 = pattern->Control0, c1 = pattern->Control1;
> DBL na = Tnormal->Amount;
>
> if ((ax >= ay) && (ax >= az))
> {
> DBL vy = quilt_cubic(fabs(y-ym),c0,c1)*sy;
> DBL vz = quilt_cubic(fabs(z-zm),c0,c1)*sz;
> nz = (nz < 0.0) ? -1 : 1;
> ny = ny + (na * vy);
> nz = nz + (na * vz);
> }
> else if ((ay >= ax) && (ay >= az))
> {
> DBL vx = quilt_cubic(fabs(x-xm),c0,c1)*sx;
> DBL vz = quilt_cubic(fabs(z-zm),c0,c1)*sz;
> nx = nx + (na * vx);
> ny = (ny < 0.0) ? -1 : 1;
> nz = nz + (na * vz);
> }
> else
> {
> DBL vx = quilt_cubic(fabs(x-xm),c0,c1)*sx;
> DBL vy = quilt_cubic(fabs(y-ym),c0,c1)*sy;
> nx = nx + (na * vx);
> ny = ny + (na * vy);
> nz = (nz < 0.0) ? -1 : 1;
> }
> normal = Vector3d(nx,ny,nz);
> normal.normalize(); // <-- this normal vector what gets updated.
> C) normal {quilted 0.5 control0 +1.0 control1 +1.0
> no_bump_scale scale 0.5}
So, as I currently understand it, if the default bump_size is 1.0, then
no_bump_scale decouples the bump_size from the scale 0.5 statement, so that the
area of the normal gets scaled, but the bump_size stays the same at 1.0 instead
of getting shrunk to 0.5 .
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
And the other thing that's throwing me off is what exactly are the function
inputs and outputs.
I was trying to graph the built-in quilted pattern before I headed out, and got
some curved inverted "V" shapes instead of anything resembling the documentation
shapes.
#declare CN = array [5] {0, 0.33, 0.5, 0.67, 1}
#local c0 = CN[0];
#for (c1, 0, 4)
#ifdef (Q) #undef Q #end
#declare Q = function {pigment {quilted control0 c0 control1 CN[c1]}}
.....
Then it struck me that the function probably isn't using linear x at the surface
of the cube where I see the pattern - it's using the vector length of <x,y,z>,
and spitting out --- a scalar.
So if I get the native pattern function worked out and graph it, I'll be sure to
LABEL THE AXES this time 'round.
'till then, hi ho, hi ho....
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 10/14/20 4:07 PM, Bald Eagle wrote:
> William F Pokorny <ano### [at] anonymous org> wrote:
>
>> I'd guess there isn't much use in translating the non-working normal.cpp
>> quilted code so
>
> Translating the non-working code would help reproduce the nonworkability.
> Then we could see where and why it doesn't work.
No doubt it might help you and perhaps others play with that code, but
suppose I believe I've already sorted through the issues with the
normal.cpp code as it was. I don't recall anything extra needed for
translation to SDL over what I posted and I know you know where the code
is based upon your questions below. :-)
>
>> below is an my initial attempt at a fix for surfaces
>> perpendicular to the x, y and z axis.
>
> But what did you fix?
All the bugs about which I previously posted - and a couple lessor about
which I did not write. ;-)
We are only handling cube and flat surfaces without distortion. There
thinking about it more the documentation - it is pretty clear the about
the application being via unit cubes.
My fix amounts to being axis-projective within each unit cube - taking
care with the polarity of the original normals and the '2D' offsets with
respect to the unit square's two center axes. Maybe we forget trying to
make 'quilted' work for other than via projection or on flat surfaces
surfaces.
Beyond that, you and I have questions as to whether the control point
graphs and descriptions are correct with respect to the pattern(1). An
update to these so they are better looking and generated with generated
POV-Ray code is a good idea no matter. Christoph often made arguments
for this and the v3.8 documentation has taken steps in this direction.
Plus, I now have cases with the no_bump_scale where I don't understand
what is happening. Your interpretation matches mine - which makes me
think there is another bug somewhere in the normals handling, but this
one probably outside quilted itself.
And I rambled a little about there being unfinished warp related normal
code. With this I expect some warps beyond transforms are not working
correctly, but I've never explored in this direction. These issues are
outside the quilted code itself in any case.
(1) - With the initial povr fix in place it looks to me as if the center
of the square face relates to control point 0 and control point 1 the
edges. One and one values is a rounded at both ends and two and two
flat. Negative values inverts the curvature so you can get for example
tile looking faces where the corners are slightly raised relative to the
centers - which I think is kinda cool.
Argh, here I am writing chapters of books again...
What to do when questions are simple; folks want simple answers, but the
situations are, with even a single feature, brutally complicated. :-(
>
>> This updated code passes most of
>> my test cases but of course has varying results with respect to curved
>> surfaces - as does the original. Whether this is what we want for a
>> best quilted fix - I don't know! I don't think we really know what the
>> original coders expected or perhaps even got to one degree or another in
>> older versions of code
>
> I'm not sure what you mean about curved surfaces - no examples have been
> provided.
>
A sphere say. For example, and though there is turbulence, you can see
the issue with the shipped quilt1 scene using the current quilted normal
implementation. The curved surface is catching parts of the cube rather
than adjusting with the surface curvature. As said above. I think we
just let this go as is for quilted. Not to say we cannot work on and
implement something better.
>> One puzzle for me is I looked at no_bump_scale in the upper right render
>> (C). I expected it to have some effect on all three surfaces, but it's
>> only changing the -x one! Not dug into code. Anyone have an idea what's
>> going on? This touches on me not being a big user of normals. Not sure
>> I've ever used no_bump_scale myself.
>
> You haven't supplied any of your scene code, so I can't tell if you have any
> scaling or offsets. The wiki says that no_bump_scale just cancels out any
> scaling of the normal depth when the texture or normal itself is scaled.
>
Yeah, sorry, I meant to say in my post I just hacked the allnormals.pov
replacing the:
#declare Quilted = normal {...}
declare with the normal{} blocks indicated. FWIW. I also changed the T
texture to read:
#declare T=texture {
pigment {rgb 1}
normal { Quilted } // <--- This
finish {phong 0.5 phong_size 20}
}
So I wouldn't have to play with animation flags.
>
> And so my first attempt at translating that was:
>
> #declare INV_SQRT_3_4 = 1.154700538;
...
> #declare IT = function (T) {1-T}
> #declare ITsqr = function (T) {pow(IT (T), 2)}
> #declare Tsqr = function (T) {pow(T, 2)}
> #declare Tcub = function (T) {pow(T, 3)}
> #declare Val0 = function (T, _P1, _P2) {
> (
> pow(T, 3) +
> (3 * T * pow(1-T, 2) * _P1) +
> (3 * pow(T,2) * (T - pow(T, 2)) * _P2)
> )
> * INV_SQRT_3_4
>
> }
>
To my eye that looks good. I'll give it a try an maybe code up and
in-built using the original c++ coding and compare to be paranoid. I see
wanting to see this as a pigment (easier in povr due negative values).
Not sure what you are after with the normal{} test...
>
> 2. There's some interface problem between the output of the function and the
> rest of what happens to that information after it gets evaluated and sent down
> the ray / surface rendering pipeline.
Yes. One apparent in the initial "DBL it=(1-t);" the function is
expecting inputs in the range of 0 to 1 because it's inverting on that
range, but we are not providing it exactly that range(2). In fact in the
normal version the value strengths passed are varying as we move a
surface along the axis in the cube.
(2) - And neither am I in my initial re-code. This maybe needs
adjustment...
It has 360 degrees of directions to get perturbed in.
And that's a problem. It needs to be perturb only in the half sphere of
the original surface normal. Something I think my code addresses.
>
> I'd also need the following three statements in c++ syntax decrypted, so I could
> try translating those into SDL.
>
> const QuiltedPattern *pattern =
> dynamic_cast<QuiltedPattern*>(Tnormal->pattern.get());
>
> POV_PATTERN_ASSERT(pattern);
>
> and
>
> normal += (DBL)Tnormal->Amount * value;
>
The first two amoung to getting the correct object pattern pointer type
to get access to the two control values. This is one place where my povr
code had already diverged. In my code this is coded:
POV_PATTERN_ASSERT(dynamic_cast<QuiltedPattern*>(Tnormal->pattern.get())
!= nullptr);
const QuiltedPattern *pattern =
static_cast<QuiltedPattern*>(Tnormal->pattern.get());
so we only take the hit of the dynamic_cast run time checking if certain
debug settings are on during a compile. The POV_PATTERN_ASSERT does
nothing in a regular compile. (Aside: one thing I noticed in the future
debian work is they currently have such a debug enabled version of
povray as possible install version.)
Ah, dang. And your question about "normal += (DBL)Tnormal->Amount *
value;" makes obvious I forgot to do that step in my re-code! Thanks. I
was getting a normal scaling of 1.0 despite coding 0.5 due this. :-)
Oh, that statement is adding an adjustment vector - one scaled by the
normal patterns sizing value (and/or bump_size in at least some
patterns) - to the original surface normal. The is the "perturb the
normal" step.
...
>
> So, as I currently understand it, if the default bump_size is 1.0, then
> no_bump_scale decouples the bump_size from the scale 0.5 statement, so that the
> area of the normal gets scaled, but the bump_size stays the same at 1.0 instead
> of getting shrunk to 0.5 .
>
Thanks. Guess I need to dig into the cause for the asymmetry in
application seen here.
Bill P. org> wrote:
>
>> I'd guess there isn't much use in translating the non-working normal.cpp
>> quilted code so
>
> Translating the non-working code would help reproduce the nonworkability.
> Then we could see where and why it doesn't work.
No doubt it might help you and perhaps others play with that code, but
suppose I believe I've already sorted through the issues with the
normal.cpp code as it was. I don't recall anything extra needed for
translation to SDL over what I posted and I know you know where the code
is based upon your questions below. :-)
>
>> below is an my initial attempt at a fix for surfaces
>> perpendicular to the x, y and z axis.
>
> But what did you fix?
All the bugs about which I previously posted - and a couple lessor about
which I did not write. ;-)
We are only handling cube and flat surfaces without distortion. There
thinking about it more the documentation - it is pretty clear the about
the application being via unit cubes.
My fix amounts to being axis-projective within each unit cube - taking
care with the polarity of the original normals and the '2D' offsets with
respect to the unit square's two center axes. Maybe we forget trying to
make 'quilted' work for other than via projection or on flat surfaces
surfaces.
Beyond that, you and I have questions as to whether the control point
graphs and descriptions are correct with respect to the pattern(1). An
update to these so they are better looking and generated with generated
POV-Ray code is a good idea no matter. Christoph often made arguments
for this and the v3.8 documentation has taken steps in this direction.
Plus, I now have cases with the no_bump_scale where I don't understand
what is happening. Your interpretation matches mine - which makes me
think there is another bug somewhere in the normals handling, but this
one probably outside quilted itself.
And I rambled a little about there being unfinished warp related normal
code. With this I expect some warps beyond transforms are not working
correctly, but I've never explored in this direction. These issues are
outside the quilted code itself in any case.
(1) - With the initial povr fix in place it looks to me as if the center
of the square face relates to control point 0 and control point 1 the
edges. One and one values is a rounded at both ends and two and two
flat. Negative values inverts the curvature so you can get for example
tile looking faces where the corners are slightly raised relative to the
centers - which I think is kinda cool.
Argh, here I am writing chapters of books again...
What to do when questions are simple; folks want simple answers, but the
situations are, with even a single feature, brutally complicated. :-(
>
>> This updated code passes most of
>> my test cases but of course has varying results with respect to curved
>> surfaces - as does the original. Whether this is what we want for a
>> best quilted fix - I don't know! I don't think we really know what the
>> original coders expected or perhaps even got to one degree or another in
>> older versions of code
>
> I'm not sure what you mean about curved surfaces - no examples have been
> provided.
>
A sphere say. For example, and though there is turbulence, you can see
the issue with the shipped quilt1 scene using the current quilted normal
implementation. The curved surface is catching parts of the cube rather
than adjusting with the surface curvature. As said above. I think we
just let this go as is for quilted. Not to say we cannot work on and
implement something better.
>> One puzzle for me is I looked at no_bump_scale in the upper right render
>> (C). I expected it to have some effect on all three surfaces, but it's
>> only changing the -x one! Not dug into code. Anyone have an idea what's
>> going on? This touches on me not being a big user of normals. Not sure
>> I've ever used no_bump_scale myself.
>
> You haven't supplied any of your scene code, so I can't tell if you have any
> scaling or offsets. The wiki says that no_bump_scale just cancels out any
> scaling of the normal depth when the texture or normal itself is scaled.
>
Yeah, sorry, I meant to say in my post I just hacked the allnormals.pov
replacing the:
#declare Quilted = normal {...}
declare with the normal{} blocks indicated. FWIW. I also changed the T
texture to read:
#declare T=texture {
pigment {rgb 1}
normal { Quilted } // <--- This
finish {phong 0.5 phong_size 20}
}
So I wouldn't have to play with animation flags.
>
> And so my first attempt at translating that was:
>
> #declare INV_SQRT_3_4 = 1.154700538;
...
> #declare IT = function (T) {1-T}
> #declare ITsqr = function (T) {pow(IT (T), 2)}
> #declare Tsqr = function (T) {pow(T, 2)}
> #declare Tcub = function (T) {pow(T, 3)}
> #declare Val0 = function (T, _P1, _P2) {
> (
> pow(T, 3) +
> (3 * T * pow(1-T, 2) * _P1) +
> (3 * pow(T,2) * (T - pow(T, 2)) * _P2)
> )
> * INV_SQRT_3_4
>
> }
>
To my eye that looks good. I'll give it a try an maybe code up and
in-built using the original c++ coding and compare to be paranoid. I see
wanting to see this as a pigment (easier in povr due negative values).
Not sure what you are after with the normal{} test...
>
> 2. There's some interface problem between the output of the function and the
> rest of what happens to that information after it gets evaluated and sent down
> the ray / surface rendering pipeline.
Yes. One apparent in the initial "DBL it=(1-t);" the function is
expecting inputs in the range of 0 to 1 because it's inverting on that
range, but we are not providing it exactly that range(2). In fact in the
normal version the value strengths passed are varying as we move a
surface along the axis in the cube.
(2) - And neither am I in my initial re-code. This maybe needs
adjustment...
It has 360 degrees of directions to get perturbed in.
And that's a problem. It needs to be perturb only in the half sphere of
the original surface normal. Something I think my code addresses.
>
> I'd also need the following three statements in c++ syntax decrypted, so I could
> try translating those into SDL.
>
> const QuiltedPattern *pattern =
> dynamic_cast<QuiltedPattern*>(Tnormal->pattern.get());
>
> POV_PATTERN_ASSERT(pattern);
>
> and
>
> normal += (DBL)Tnormal->Amount * value;
>
The first two amoung to getting the correct object pattern pointer type
to get access to the two control values. This is one place where my povr
code had already diverged. In my code this is coded:
POV_PATTERN_ASSERT(dynamic_cast<QuiltedPattern*>(Tnormal->pattern.get())
!= nullptr);
const QuiltedPattern *pattern =
static_cast<QuiltedPattern*>(Tnormal->pattern.get());
so we only take the hit of the dynamic_cast run time checking if certain
debug settings are on during a compile. The POV_PATTERN_ASSERT does
nothing in a regular compile. (Aside: one thing I noticed in the future
debian work is they currently have such a debug enabled version of
povray as possible install version.)
Ah, dang. And your question about "normal += (DBL)Tnormal->Amount *
value;" makes obvious I forgot to do that step in my re-code! Thanks. I
was getting a normal scaling of 1.0 despite coding 0.5 due this. :-)
Oh, that statement is adding an adjustment vector - one scaled by the
normal patterns sizing value (and/or bump_size in at least some
patterns) - to the original surface normal. The is the "perturb the
normal" step.
...
>
> So, as I currently understand it, if the default bump_size is 1.0, then
> no_bump_scale decouples the bump_size from the scale 0.5 statement, so that the
> area of the normal gets scaled, but the bump_size stays the same at 1.0 instead
> of getting shrunk to 0.5 .
>
Thanks. Guess I need to dig into the cause for the asymmetry in
application seen here.
Bill P.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> Beyond that, you and I have questions as to whether the control point
> graphs and descriptions are correct with respect to the pattern(1). An
> update to these so they are better looking and generated with generated
> POV-Ray code is a good idea no matter. Christoph often made arguments
> for this and the v3.8 documentation has taken steps in this direction.
Yes, I think that such a thing would help answer most of the usual questions
about implementation, syntax, limitations, artefacts and other issues, etc.
Something using #switch to control the scene would allow easy generation of the
official documentation image, but with supplemental code showing variations and
slick tricks that one can do with the pattern.
> A sphere say. For example, and though there is turbulence, you can see
> the issue with the shipped quilt1 scene using the current quilted normal
> implementation. The curved surface is catching parts of the cube rather
> than adjusting with the surface curvature. As said above. I think we
> just let this go as is for quilted. Not to say we cannot work on and
> implement something better.
I have a "quilted.pov" scene - but yes, I understand (it's what I thought).
Same as if you use checkered.
Don't you just use uv_mapping to fix that?
> To my eye that looks good. I'll give it a try an maybe code up and
> in-built using the original c++ coding and compare to be paranoid. I see
> wanting to see this as a pigment (easier in povr due negative values).
> Not sure what you are after with the normal{} test...
You said the normal had different properties / handling than the pattern. So
I'm treating them as two separate things.
> It has 360 degrees of directions to get perturbed in.
>
> And that's a problem. It needs to be perturb only in the half sphere of
> the original surface normal. Something I think my code addresses.
I mean that I don't understand exactly how a normal gets perturbed if I plug
some scalar function into a normal {} statement.
The top of a cube has a normal of +y.
If I perturb that normal, it gets tilted.
But in what direction? I STILL have a full 360 degrees of a circle to choose
from - the tilt needs to be directional, but there is no basis vector
information associated with the scalar of the function.
Does the +y get tilted in the +x direction? The +z direction?
Is it dependent on the light source or camera vector?
> Thanks. Guess I need to dig into the cause for the asymmetry in
> application seen here.
I must admit that I can't really see from your examples what the problem is -
but if you see it and it's real.... org> wrote:
> Beyond that, you and I have questions as to whether the control point
> graphs and descriptions are correct with respect to the pattern(1). An
> update to these so they are better looking and generated with generated
> POV-Ray code is a good idea no matter. Christoph often made arguments
> for this and the v3.8 documentation has taken steps in this direction.
Yes, I think that such a thing would help answer most of the usual questions
about implementation, syntax, limitations, artefacts and other issues, etc.
Something using #switch to control the scene would allow easy generation of the
official documentation image, but with supplemental code showing variations and
slick tricks that one can do with the pattern.
> A sphere say. For example, and though there is turbulence, you can see
> the issue with the shipped quilt1 scene using the current quilted normal
> implementation. The curved surface is catching parts of the cube rather
> than adjusting with the surface curvature. As said above. I think we
> just let this go as is for quilted. Not to say we cannot work on and
> implement something better.
I have a "quilted.pov" scene - but yes, I understand (it's what I thought).
Same as if you use checkered.
Don't you just use uv_mapping to fix that?
> To my eye that looks good. I'll give it a try an maybe code up and
> in-built using the original c++ coding and compare to be paranoid. I see
> wanting to see this as a pigment (easier in povr due negative values).
> Not sure what you are after with the normal{} test...
You said the normal had different properties / handling than the pattern. So
I'm treating them as two separate things.
> It has 360 degrees of directions to get perturbed in.
>
> And that's a problem. It needs to be perturb only in the half sphere of
> the original surface normal. Something I think my code addresses.
I mean that I don't understand exactly how a normal gets perturbed if I plug
some scalar function into a normal {} statement.
The top of a cube has a normal of +y.
If I perturb that normal, it gets tilted.
But in what direction? I STILL have a full 360 degrees of a circle to choose
from - the tilt needs to be directional, but there is no basis vector
information associated with the scalar of the function.
Does the +y get tilted in the +x direction? The +z direction?
Is it dependent on the light source or camera vector?
> Thanks. Guess I need to dig into the cause for the asymmetry in
> application seen here.
I must admit that I can't really see from your examples what the problem is -
but if you see it and it's real....
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
So here's what I'm getting out of
function {pigment {quilted control0 c0 control1 CN[c1]}}
and varying all components of the input vector from 0 to 1 at the same time.
#for (X, 0, 1, 0.01)
#local QX = Q (X, X, X);
plots of QX.x QX.y and QX.z are all the same, and the transmit and filter
components are always 0
So I have no idea where the documentation graphs come from.
I _must_ be doing _something_ wrong....
Post a reply to this message
Attachments:
Download 'quilteddocumentation_38.png' (78 KB)
Preview of image 'quilteddocumentation_38.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
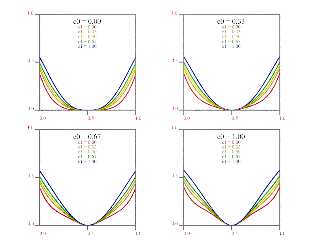
So I wanted to check on the size and position of the pattern, given the graphs
in the docs go from -0.5 to 0.5.
The base pattern exists in a cube from <0, 0, 0> to <1, 1, 1>.
Which means it's centered at <0.5, 0.5, 0.5>, and the graph must be showing a
sort of signed axial distance.
But the function NEVER attains a value of 1.
Just to "see it all", I rendered 20 isosurfaces of 'quilted' with thresholds
from 0 to 1.
It just doesn't jive with the graphs showing a function returning values of from
0 to 1 inclusive. Nor with the changing shape of the curves.
(And I did loop through and evaluate all of the c0 and c1 values and just plot
them all on top of one another. Nothing reached 1, nothing stood out as an
S-shaped curve.)
It _does_ agree with the graphs I made showing it topping out at ~0.55.
Lucy... you got some 'splainin' to do....
Post a reply to this message
Attachments:
Download 'quilteddimensions.png' (46 KB)
Preview of image 'quilteddimensions.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 10/15/20 3:13 PM, Bald Eagle wrote:
> William F Pokorny <ano### [at] anonymous org> wrote:
>
...
>
I'll attempt to respond to your recent questions with this post while
rambling too about what I've recently come to understand.
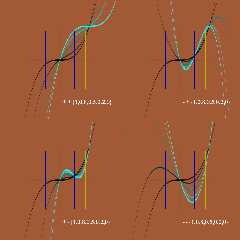
First, I think we missed a mistake in the translation of quilt_cubic. I
believe the correct SDL is:
#declare INV_SQRT_3_4 = 1.154700538; // 1.0/sqrt(3.0/4.0) used in povr
#declare IT = function (T) {1-T}
#declare ITsqr = function (T) {pow(IT (T), 2)}
#declare Tsqr = function (T) {pow(T, 2)}
#declare Tcub = function (T) {pow(T, 3)}
#declare Val0 = function (T, _P1, _P2) {
(
pow(T, 3) +
(3 * T * pow(1-T, 2) * _P1) +
(3 * pow(T,2) * (1-T) * _P2)
)
* INV_SQRT_3_4
}
I've attached an image of 4 renders using iosurfaces of the function to
plot. In each plotting results using x at T and using different set
control magnitudes. In each of the four flip the polarity of the control
points as indicated.
Here speaking about the true normal vector perturbation method - ie
normal {quilted..} - what I'm interested in for povr. The old quilted
sent values to quilt_cubic in the range of 0 to 0.867. This is the
yellow vertical line in the plots. My initial re-code is using values
in the range of 0 to 0.5 because it seemed to work well - as do then,
negative control values. Meaning in the current re-code, -1 to 1
control1 and control2 values are OK. Larger magnitudes can be used too,
but results less and less real world like - especially in the negative
direction. (Negative control values 'function' in the current v3.8
quilted too)
At it's best, the old true normal quilted looks a little more
quilted/pillow-y than my current re-code, but the re-code offers much
more stable results. Plus, you can now get other effects with wacko
control values. I've attached a second image with a v38 render (noisy)
and a povr render with the control values set to +9.6 and -9.6.
---
On the issue I was seeing with no_bump_scale. I saw what I saw because
of a typo in my original re-code. A typo which caused the +-x axis to
work as usual! Once I stopped trying to internally normalize all 3
dimensions, things work as before for no_bump_scale.
The no_bump_scale turns off the normalization of the incoming surface
normal. Because we are perturbing incoming normals with the true normal
patterns, using the option affects the strength of the perturbation for
all scales not 1 in magnitude. The 'bump_size' value does too - as does
any non-symmetric scaling. The normal perturbation path can be
complicated.
When normals are used in ray direction and color calculations, they are
always normalized to a length of 1.0. In other words, the magnitude of
the normal doesn't matter at this point. Everything we do perturbing
normals has to do with setting the resultant normal direction(a).
(a) - Excepting setting the normal strength to 0 which nulls the normal
effects - though as I write this, I'm unsure what happens with ior
calculations when the normal is zeroed...
Partly by the feature name, I suspect no_bump_scale was first aimed at
bump maps where the depth of the normal at each vertex in patch based
surfaces gets interpolated with the normals on the other corners of the
patch. Some tooling does this in any case.
I'm unsure what happens with triangles and normal interpolation in
POV-Ray with respect to normal magnitudes? Anyone know? When I've played
myself with meshes and setting normals, I've always normalized them.
------- Your questions.
> Don't you just use uv_mapping to fix that?
Yes, that is a way to get what you want for shapes with uv mapping. In
POV-Ray there are often many ways to approach some result. ;-)
> How the normal pattern perturbation works?
My current understanding...
For true normal patterns, essentially, an adder vector is calculated
then weighted by the normal strength / bump_size value (0.5 default)
before it gets added to the incoming surface normal. That incoming
normal may or may not have been normalized depending upon the
no_bump_scale setting.
For "value for map" based normals the values are perturbed and this
affects the pyramid of samples around the surface point and so the
resultant normal direction. I think the no_bump_scale must do nothing
then? - but I've not tested this thought. It is with this form the
normal accuracy default or user setting is used.
> How to explain the -0.5 to 0.5 bottom axis of the plots in the
documentation?
Not sure. Perhaps the values intended to represent the +-magnitudes of
the possible x, y and z offsets from the center of each cube into the
function. So a graph not really a function graph, but something meant to
help users understand quilted? I now lean toward a c0,c1 grid of results
(-1,+1) as a guide over plots of an internal function used in part to
get some final effect.
Bill P. org> wrote:
>
...
>
I'll attempt to respond to your recent questions with this post while
rambling too about what I've recently come to understand.
First, I think we missed a mistake in the translation of quilt_cubic. I
believe the correct SDL is:
#declare INV_SQRT_3_4 = 1.154700538; // 1.0/sqrt(3.0/4.0) used in povr
#declare IT = function (T) {1-T}
#declare ITsqr = function (T) {pow(IT (T), 2)}
#declare Tsqr = function (T) {pow(T, 2)}
#declare Tcub = function (T) {pow(T, 3)}
#declare Val0 = function (T, _P1, _P2) {
(
pow(T, 3) +
(3 * T * pow(1-T, 2) * _P1) +
(3 * pow(T,2) * (1-T) * _P2)
)
* INV_SQRT_3_4
}
I've attached an image of 4 renders using iosurfaces of the function to
plot. In each plotting results using x at T and using different set
control magnitudes. In each of the four flip the polarity of the control
points as indicated.
Here speaking about the true normal vector perturbation method - ie
normal {quilted..} - what I'm interested in for povr. The old quilted
sent values to quilt_cubic in the range of 0 to 0.867. This is the
yellow vertical line in the plots. My initial re-code is using values
in the range of 0 to 0.5 because it seemed to work well - as do then,
negative control values. Meaning in the current re-code, -1 to 1
control1 and control2 values are OK. Larger magnitudes can be used too,
but results less and less real world like - especially in the negative
direction. (Negative control values 'function' in the current v3.8
quilted too)
At it's best, the old true normal quilted looks a little more
quilted/pillow-y than my current re-code, but the re-code offers much
more stable results. Plus, you can now get other effects with wacko
control values. I've attached a second image with a v38 render (noisy)
and a povr render with the control values set to +9.6 and -9.6.
---
On the issue I was seeing with no_bump_scale. I saw what I saw because
of a typo in my original re-code. A typo which caused the +-x axis to
work as usual! Once I stopped trying to internally normalize all 3
dimensions, things work as before for no_bump_scale.
The no_bump_scale turns off the normalization of the incoming surface
normal. Because we are perturbing incoming normals with the true normal
patterns, using the option affects the strength of the perturbation for
all scales not 1 in magnitude. The 'bump_size' value does too - as does
any non-symmetric scaling. The normal perturbation path can be
complicated.
When normals are used in ray direction and color calculations, they are
always normalized to a length of 1.0. In other words, the magnitude of
the normal doesn't matter at this point. Everything we do perturbing
normals has to do with setting the resultant normal direction(a).
(a) - Excepting setting the normal strength to 0 which nulls the normal
effects - though as I write this, I'm unsure what happens with ior
calculations when the normal is zeroed...
Partly by the feature name, I suspect no_bump_scale was first aimed at
bump maps where the depth of the normal at each vertex in patch based
surfaces gets interpolated with the normals on the other corners of the
patch. Some tooling does this in any case.
I'm unsure what happens with triangles and normal interpolation in
POV-Ray with respect to normal magnitudes? Anyone know? When I've played
myself with meshes and setting normals, I've always normalized them.
------- Your questions.
> Don't you just use uv_mapping to fix that?
Yes, that is a way to get what you want for shapes with uv mapping. In
POV-Ray there are often many ways to approach some result. ;-)
> How the normal pattern perturbation works?
My current understanding...
For true normal patterns, essentially, an adder vector is calculated
then weighted by the normal strength / bump_size value (0.5 default)
before it gets added to the incoming surface normal. That incoming
normal may or may not have been normalized depending upon the
no_bump_scale setting.
For "value for map" based normals the values are perturbed and this
affects the pyramid of samples around the surface point and so the
resultant normal direction. I think the no_bump_scale must do nothing
then? - but I've not tested this thought. It is with this form the
normal accuracy default or user setting is used.
> How to explain the -0.5 to 0.5 bottom axis of the plots in the
documentation?
Not sure. Perhaps the values intended to represent the +-magnitudes of
the possible x, y and z offsets from the center of each cube into the
function. So a graph not really a function graph, but something meant to
help users understand quilted? I now lean toward a c0,c1 grid of results
(-1,+1) as a guide over plots of an internal function used in part to
get some final effect.
Bill P.
Post a reply to this message
Attachments:
Download 'cubic_quilt_story.png' (123 KB)
Download 'v38_vs_povr_pn9pt6.png' (224 KB)
Preview of image 'cubic_quilt_story.png'
Preview of image 'v38_vs_povr_pn9pt6.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()