Illustration re:
http://news.povray.org/povray.general/thread/%3Cweb.56ea1f7e7eb839c15e7df57c0%40news.povray.org%3E/

######################################################################


#version 3.7;


global_settings{ assumed_gamma 1.0 }

#include "debug.inc"
 Set_Debug (true)
#include "colors.inc"
#include "textures.inc"
#include "shapes.inc"
#include "shapes2.inc"
#include "functions.inc"
#include "math.inc"
#include "transforms.inc"


light_source { <0, 150, 0>  color rgb <1, 1, 1>}


#declare Camera_Top = camera {
                            location  <0, 4, -0.01>
                            //right    x*image_width/image_height
                            look_at   <0, 0, 0>}

#declare Camera_Front = camera {
                            location  <5, 20, -20>
                            //right    x*image_width/image_height
                            look_at   <5, 10, 0>}

camera {Camera_Top}

plane {y, 0 pigment {White}}

#declare T1 = 0.01;   // Line widths
#declare T2 = 0.005;
#declare MarkerCircle = 0.012;


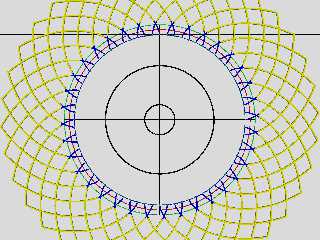
#declare Teeth = 36;     #declare N = Teeth;   // Number of teeth on gear (N)
#declare Pitch = 24;     #declare P = Pitch;   // Gear pitch (P)

#declare RootCircle = (Teeth-2)/Pitch;  #declare RD = RootCircle; // Root circle
diameter (RD)
#declare PitchCircle = Teeth/Pitch;  #declare D = PitchCircle; // Pitch circle
diameter (D)
#declare OutsideCircle= (Teeth+2)/Pitch; #declare OD = OutsideCircle; // Outside
circle diameter (OD)

#declare Hub = 0.9;
#declare Hole = 0.25;

torus {RootCircle,    T2  translate <0, T1, 0> texture {pigment {color Blue}
finish {phong 0.1}} }  // RootCircle Circle
torus {PitchCircle,   T2  translate <0, T1, 0> texture {pigment {color Red}
finish {phong 0.1}} }  // RootCircle Circle
torus {OutsideCircle, T2  translate <0, T1, 0> texture {pigment {color Green}
finish {phong 0.1}} }  // OutsideCircle Circle

torus {Hub, T1  translate <0, T1, 0> texture {pigment {color Black} finish
{phong 0.1}} }  // Recessed Hub Circle
torus {Hole, T1  translate <0, T1, 0> texture {pigment {color Black} finish
{phong 0.1}} }  // Shaft hole
// Center marker
cylinder {<-OutsideCircle, T1, 0>, <OutsideCircle, T1, 0> T2 texture {pigment
{color Black} finish {phong 0.1}} }
cylinder {<0, T1, -OutsideCircle>, <0, T1, OutsideCircle> T2 texture {pigment
{color Black} finish {phong 0.1}} }
cylinder {<-OutsideCircle*2, T1, RootCircle>, <OutsideCircle*2, T1, RootCircle>
T2 texture {pigment {color Black} finish {phong 0.1}} }

#declare CircularThicknessAngle = (360/N)*0.5;      // Circular Thickness Angle
0.5 because teeth AND spaces

#declare Degrees = 90;     // Degrees to rotate through involute
#declare Radians = Degrees * pi/180;  // Radians to rotate through involute

#declare AngularSpacing = 360/Teeth;  // How many degrees to rotate involute
curves for next tooth



#for (Tooth1, 0, Teeth)
 #declare Tooth2 = Tooth1 + 0.5;

 #for (theta, 0, Radians, 0.001)
  #declare X = RootCircle * (cos(theta) + theta*sin(theta));
  #declare Z1 = RootCircle * (sin(theta) - theta*cos(theta));
  #declare Z2 = -RootCircle * (sin(theta) - theta*cos(theta));     // Opposite
side of involute tooth
  sphere{ <X, T1, Z1>, T1 pigment {Blue} rotate -y*Tooth1*AngularSpacing}
  sphere{ <X, T1, Z2>, T1 pigment {Blue} rotate -y*Tooth2*AngularSpacing}

  #declare Distance1 = sqrt (pow (X,2) + pow (Z1,2));  // radius at this point
in the plotting of the gear tooth
  // check if at RootCircle Circle
  #if (  theta = sqrt (abs ((Distance1 / RootCircle) - 1) )   )
  sphere{ <X, T1, Z1>, MarkerCircle pigment {Green} rotate
-y*Tooth1*AngularSpacing}
  sphere{ <X, T1, Z2>, MarkerCircle pigment {Green} rotate
-y*Tooth2*AngularSpacing}
  #end

  // check if at OutsideCircle Circle
  #if (  theta > sqrt ((pow (OutsideCircle, 2) - pow (RootCircle, 2)) /
RootCircle)   ) // Seems broken.  Thanks, M.I.T  :|
  sphere{ <X, T1, Z1>, MarkerCircle pigment {Yellow} rotate
-y*Tooth1*AngularSpacing}
  sphere{ <X, T1, Z2>, MarkerCircle pigment {Yellow} rotate
-y*Tooth2*AngularSpacing}
  #end

  /* check if involutes cross
  #declare NegInvolute = transform {rotate <0, -AngularSpacing, 0>};
  #declare NI_Point = vtransform (<X, T1, Z2>, NegInvolute);
  #if ( abs(NI_Point.z) - abs(Z1) < 0.1)
  sphere{ <X, T1, Z1>, MarkerCircle pigment {Gray50} rotate
-y*Tooth1*AngularSpacing}
  //sphere{ <X, T1, Z2>, MarkerCircle pigment {Green} rotate
-y*Tooth2*AngularSpacing}
  #end
  */
 #end


#end // end for

Post a reply to this message

Attachments:
Download 'involute.png' (120 KB)

Preview of image 'involute.png'

OK,
I recognized the obvious solution to the Outer Circle intersection, implemented
a practical While Loop to terminate the involutes, used a Lohmueller segment of
a torus to connect the roots of the teeth, and topped off the teeth with a
straight cylinder.

Looks ok with teeth of 36 and 60, although I expected the teeth to be thicker
and have less space between them in meshing gears.

Still need to ponder visualizing the "line of action" where the teeth mesh.
Also need to figure out how best to do this in CSG,
and what curve works best for doing this in SVG.

Post a reply to this message

Attachments:
Download 'involute.png' (61 KB)

Preview of image 'involute.png'

Close up showing layout lines and intersection points.   :)

Post a reply to this message

Attachments:
Download 'involute.png' (57 KB)

Preview of image 'involute.png'

Le 17/03/2016 23:00, Bald Eagle a écrit :
> Close up showing layout lines and intersection points.   :)
> 
The mechanic teaching in me, old enough just have to complain:

the top part of a teeth must never be close to the bottom part of the opposite gear.

IIRC, if top part (difference of radius betweeen red and green) circle is 1, the
bottom part (grey and red) should be 1.25.

And unless you have a specially made gear, the perpendicular straight line to the
black line
(which start at the red line ?) should be the line on which the teeth of each gear get
in contact
(on the side on which the energy is transmitted, the other side of the tooth is not
used until
the movement is reversed)

The interest of the involute is that the contact point moves as gears rotate *without*
friction.

You are correct: you have a problem with the width of the tooth.

Despite the name of "metric", the following page might help:

http://www.metrication.com/engineering/gears.html

Notice the Dedendum is Height - Addendum, Addendum = 1 * module, Height = 2.25 or 2.4
* module.

And despite the top schema, the outer circle of one gear does not match the inner
circle of the other. Never.
If it was, the smallest particle at the top of a tooth would block the system when
crunched in the pit.

Post a reply to this message

Le 18/03/2016 07:59, Le_Forgeron a écrit :

And I forgot: the involute starts from the red circle outward. The inner 
part of the tooth can be a radial line, curved according to the tools 
needed to remove the metal to join the most inner circle.
(at least as long as the number of teeth of each gear is big enough. 
gears with few teeth (like 12 or less) need more caution on the inner part.)

Post a reply to this message

> OK,
> I recognized the obvious solution to the Outer Circle intersection, implemented
> a practical While Loop to terminate the involutes, used a Lohmueller segment of
> a torus to connect the roots of the teeth, and topped off the teeth with a
> straight cylinder.
>
> Looks ok with teeth of 36 and 60, although I expected the teeth to be thicker
> and have less space between them in meshing gears.
>
> Still need to ponder visualizing the "line of action" where the teeth mesh.
> Also need to figure out how best to do this in CSG,
> and what curve works best for doing this in SVG.

It's been over a decade since I did this stuff at University, and a good 
few years since I used it at work. However I did find this link in my 
"useful" folder on my work PC, maybe it helps in some way:

https://www.bostongear.com/pdf/gear_theory.pdf

Post a reply to this message

Le_Forgeron <jgr### [at] freefr> wrote:

> the top part of a teeth must never be close to the bottom part of the opposite gear.
> IIRC, if top part (difference of radius between red and green) circle is 1, the
> bottom part (grey and red) should be 1.25.

Yes, I would agree that there needs to be more [any] clearance between the teeth
of one gear and the body of the other.   I'm progressing towards that.

> And unless you have a specially made gear, the perpendicular straight line to the
black line
> (which start at the red line ?) should be the line on which the teeth of each gear
get in contact
Right the gears ought to meet where the red circles are tangent, and "roll"
along a line that is tangent to both base circles - which makes it normal to
both involutes at that point.  I'm working on illustrating that.

> You are correct: you have a problem with the width of the tooth.

I'll look through that - I've probably seen 100 similar pages, but that doesn't
help me "put it all together" especially when a lot of things are interrelated,
and changing one thing then changes 5 others.  So, this will likely be an
intermittent mix of progress, error, and correction.

> And despite the top schema, the outer circle of one gear does not match the inner
circle of the other. Never.
> If it was, the smallest particle at the top of a tooth would block the system when
crunched in the pit.

Yes.  I have yet to add any clearance, and I need to learn more about how to
construct an undercut.
I found this fascinating page:
http://www.codeproject.com/Articles/1037482/Drawing-Gears-Circular-and-Non-Circular
But apparently the code may need some fixing to run.  I can read it and learn
from it though  :)


Thanks for keeping an eye on things and keeping me on course.
There is always so much to learn.

Post a reply to this message

scott <sco### [at] scottcom> wrote:

> It's been over a decade since I did this stuff at University, and a good
> few years since I used it at work. However I did find this link in my
> "useful" folder on my work PC, maybe it helps in some way:
>
> https://www.bostongear.com/pdf/gear_theory.pdf

Thanks, Scott.  You anticipated where I'm going with this - I'm sure I've seen
that page many times over the last year - I just never got around to starting
the gear model.

Hopefully that helps me to not only understand and further lay out the next
level of detail, but helps me think ahead to parameterizing the code.  I noticed
that for low tooth numbers, my code starts to unravel and the teeth look like
someone twisted them 180 with a very big pair of Vice-Grips.

Post a reply to this message