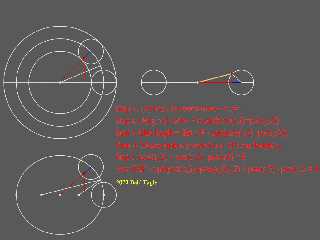
 |
|
|
|
|
|
| |
| |
|
|
|
|
| |
| |
|
|
So, just to provide a diagram for the elliptical torus, we can see that the same
sort of situation exists, and the same calculations are used once we establish a
length from the origin to point P.
And I think that's where things get interesting (complicated).
https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/deriving-the-equation-of-an-ellipse-centered-at-the-or
igin/
describes how the definition of a torus (constant distance from two foci) gets
algebraically converted down to pow(x,2)/pow(a,2) + pow(y,2)/pow(b,2) = 1.
But really what we want is a distance function for the points on an ellipse.
I found this excellent answer for how to do that
https://math.stackexchange.com/q/1760296
so since the distance is sqrt(pow(x,2)+pow(y,2)), I use the equations from that
post to substitute in for x and y in the distance function to get:
#declare DistE = function (x, y, z, a, b){
sqrt (
(pow(a,2)*pow(b,2)*pow(x,2))/((pow(b,2)*pow(x,2))+(pow(a,2)*pow(y,2))) +
(pow(a,2)*pow(b,2)*pow(y,2))/((pow(b,2)*pow(x,2))+(pow(a,2)*pow(y,2)))
)
}
and then plug that into the main isosurface equation for an elliptical torus
with a constant circular cross-section.
#declare IET =
function (x,y,z,a,b,r) {
pow(DistE(x,y,z,a,b) - sqrt(pow(x,2)+pow(y,2)) ,2) + pow(z,2) - pow(r,2)
}
But I still get no visible surface.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Helps to provide the diagram...
Post a reply to this message
Attachments:
Download 'implicitellipticaltorus.png' (130 KB)
Preview of image 'implicitellipticaltorus.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
So, I looped over x, y, and z and sent the evaluated function result to the
debug stream. Massive delay from sending 8000 points to the text stream
later...
and I get values in the hundreds, less, less, less, and maybe a min of 0 or so.
I then plotted points with a value of 10 or less with spheres.
There's definitely an elliptical shape in there somewhere....
Post a reply to this message
Attachments:
Download 'implicitellipticaltorus.png' (119 KB)
Preview of image 'implicitellipticaltorus.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Oh look:
If I clean up my sloppy code and cease engaging in flagrant dumbassery.....
Post a reply to this message
Attachments:
Download 'implicitellipticaltorus.png' (148 KB)
Preview of image 'implicitellipticaltorus.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
And wow - wouldn't you know - when you actually do the math correctly, it comes
out dead-on.
:)
f_elliptical_torus in the proper x-z plane
Post a reply to this message
Attachments:
Download 'implicitellipticaltorus.png' (93 KB)
Preview of image 'implicitellipticaltorus.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 5/4/20 8:08 PM, Bald Eagle wrote:
> And wow - wouldn't you know - when you actually do the math correctly, it comes
> out dead-on.
>
> :)
>
> f_elliptical_torus in the proper x-z plane
>
Cool! :-)
I'm going make another attempt at an inbuilt function for this. If
you've tweaked something in the code from the previous few posts, please
let me know.
More ReL (Real Life) than RaL (Ray Life) today - so likely later this
week before I get to it.
Bill P.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
William F Pokorny <ano### [at] anonymous org> wrote:
> I'm going make another attempt at an inbuilt function for this. If
> you've tweaked something in the code from the previous few posts, please
> let me know.
Nope - Just been playing around with it a bit to make sure the outer and inner
shapes are truly elliptical (they are).
I know we have a vlength() - but it can't be used in functions (vector
argument).
Maybe if there was a way to just do a Vlength (x,y,z) to get around that...
I was also thinking that non-circular cross sections would be something nice to
have - something like the form factors for the helix functions. I have one
function that I'll try to work out for that, but other functions similar to the
superellipsoid, "squircle", and rounded box seem like they would have utility
for povvers as well.
Conversely, It would be great to have a "torus" that was spherical or
ellipsoidal - but could follow the shape of some other function or spline.
With regard to dot notations and vectors - what is the "native form" for a
pigment pattern? Is it an "rgb" vector where each component simply has the same
value unless modified by a color_map?
And is it therefore slower to use .gray or .hf?
> More ReL (Real Life) than RaL (Ray Life) today - so likely later this
> week before I get to it.
So much ReL. Juggling Arduino, work, home, and COVID ridiculousness.
No worries - take your time. :)
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
"Bald Eagle" <cre### [at] netscapenet> wrote:
> I was also thinking that non-circular cross sections would be something nice to
> have - something like the form factors for the helix functions. I have one
> function that I'll try to work out for that, but other functions similar to the
> superellipsoid, "squircle", and rounded box seem like they would have utility
> for povvers as well.
I made excellent progress in translating the function of main interest to into a
pattern and an isosurface. I think in order to make it function as a
cross-sectional term, it needs to "translate its frame of reference to the
origin", and so I might need to convert the atan2 function to a polynomial.
But I might be wrong about that.
Essentially, I need to calculate the _angle_ that I'm at around the cross
section using x and y....
So I'd need to do something like this, only in SDL.
from:
https://stackoverflow.com/questions/11930594/calculate-atan2-without-std-functions-or-c99
float normalized_atan2( float y, float x )
{
static const uint32_t sign_mask = 0x80000000;
static const float b = 0.596227f;
// Extract the sign bits
uint32_t ux_s = sign_mask & (uint32_t &)x;
uint32_t uy_s = sign_mask & (uint32_t &)y;
// Determine the quadrant offset
float q = (float)( ( ~ux_s & uy_s ) >> 29 | ux_s >> 30 );
// Calculate the arctangent in the first quadrant
float bxy_a = ::fabs( b * x * y );
float num = bxy_a + y * y;
float atan_1q = num / ( x * x + bxy_a + num );
// Translate it to the proper quadrant
uint32_t uatan_2q = (ux_s ^ uy_s) | (uint32_t &)atan_1q;
return q + (float &)uatan_2q;
}
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
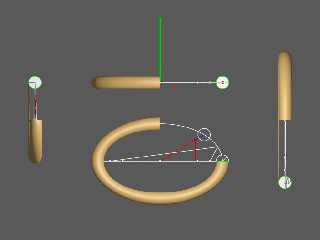
Scratch that initial misconception.
> Essentially, I need to calculate the _angle_ that I'm at around the cross
> section using x and y....
Which means that I need to unravel the dot product between two vectors.
The first vector being the normalized blue segment in the drawing.
The second vector being the normalized radial vector in the vertical plane of
the blue vector.
Got some cool screw-ups, and have some visual confirmation that I can get a nice
non-circular/elliptic shape to the R of the torus.
Maybe I'll get it before tomorrow afternoon.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Grrr.
Tried like 5 different ways, and wrote functions for cos, vlength, norm, dot,
and angle.
I just get the same results - modification of the R, not the r.
Maybe it will come to me with more sleep.
The rear row are single instances of the shapes - like the spherical pattern,
instead of multiple level sets of the isosurfaces like the onion.
Anyway, here's a preview to show the direction I'm heading.
Post a reply to this message
Attachments:
Download 'ngonisosurface.png' (175 KB)
Preview of image 'ngonisosurface.png'
|
|
| |
| |
|
|
|
|
| |
|
|
