 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
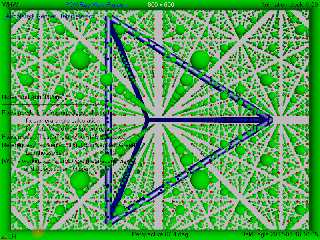
I worked a lot of what I needed out, and it mostly works the way I want it to.
Still a few small things that I haven't fixed / perfected.
But now I can plot out the camera's view frustum, and do some basic culling /
clipping.
Questions, comments, and suggestions for fixes & further developments welcome.
Post a reply to this message
Attachments:
Download 'viewfrustrumtest1.png' (533 KB)
Preview of image 'viewfrustrumtest1.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
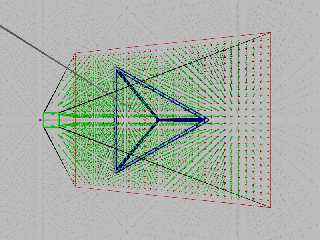
meta-view:
Post a reply to this message
Attachments:
Download 'viewfrustumtest2.png' (379 KB)
Preview of image 'viewfrustumtest2.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Working on some of this to do bounding boxes, and if that works, I might look
into octree culling.
Currently I need to figure out a quick and direct way to establish the p-vertex
and n-vertex.
https://books.google.com/books?id=CCqzMm_-WucC&pg=PA74&lpg=PA74&dq=ned+greene+frustum&source=bl&ots=mtnu29NEfj&sig=TvSJ
4OWFFaRb6c0RiSbtXD9pbww&hl=en&sa=X&ved=0ahUKEwjzsZm9mcfRAhVCOCYKHcBuCXYQ6AEIIjAB#v=onepage&q=ned%20greene%20frustum&f=f
alse
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 1/16/2017 10:17 AM, Bald Eagle wrote:
> I worked a lot of what I needed out, and it mostly works the way I want it to.
> Still a few small things that I haven't fixed / perfected.
>
> But now I can plot out the camera's view frustum, and do some basic culling /
> clipping.
>
> Questions, comments, and suggestions for fixes & further developments welcome.
>
Are you using a perspective camera or orthographic?
Mike
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Mike Horvath <mik### [at] gmail com> wrote:
> Are you using a perspective camera or orthographic?
I had hoped that the diagram would clearly show the perspective camera's frustum
- an orthographic view frustum would appear as a rectangular solid instead of a
[truncated] square-base pyramid.
I found a good an very fast method of determining the p-vertex,
http://www.txutxi.com/?p=584
but I'm currently struggling with understanding _exactly_ how planes and their
normals get calculated.
I'm using equations from Paul Bourke's site to calculate the A, B, C and (-)D
coefficients in the plane equation,
#declare Point1 = <-1, 0.5, 1>;
#declare Point2 = <1, -0.25, 1>;
#declare Point3 = <0, -1, -1>;
cylinder {Point1, Point2 0.005 texture {pigment {Black}} }
cylinder {Point2, Point3 0.005 texture {pigment {Black}} }
cylinder {Point3, Point1 0.005 texture {pigment {Black}} }
// derive the plane equation
#declare A1 = Point1.y*(Point2.z-Point3.z) + Point2.y*(Point3.z-Point1.z) +
Point3.y*(Point1.z-Point2.z);
#declare B1 = Point1.z*(Point2.x-Point3.x) + Point2.z*(Point3.x-Point1.x) +
Point3.z*(Point1.x-Point2.x);
#declare C1 = Point1.x*(Point2.y-Point3.y) + Point2.x*(Point3.y-Point1.y) +
Point3.x*(Point1.y-Point2.y);
#declare D1 = -1*(Point1.x*(Point2.y*Point3.z-Point3.y*Point2.z) +
Point2.x*(Point3.y*Point1.z-Point1.y*Point3.z) +
Point3.x*(Point1.y*Point2.z-Point2.y*Point1.z));
#declare L = vlength (<A1, B1, C1>);
and after much fiddling, got the plane to pass through the three points, and the
p-vertex to be where I think it ought to be.
I'd like to figure out the length and direction of the normal vector of the
plane, and how to calculate the position of a point in the plane that is closest
to a point not in the plane (in this case, the p-vertex).
Likely there's a way to use POV-Ray's vector functions, and macros, with
rotations and translations, but I'd like to use a direct calculation - something
that would be straight out of analytical geometry.
(I looked through Friedrich Lohmueller's site and his analytical_g.inc file, but
I didn't find exactly what I was looking for - maybe I missed it)
[I am, admittedly, probably not thinking about this in the right way, and am
thus overcomplicating it for myself as usual] com> wrote:
> Are you using a perspective camera or orthographic?
I had hoped that the diagram would clearly show the perspective camera's frustum
- an orthographic view frustum would appear as a rectangular solid instead of a
[truncated] square-base pyramid.
I found a good an very fast method of determining the p-vertex,
http://www.txutxi.com/?p=584
but I'm currently struggling with understanding _exactly_ how planes and their
normals get calculated.
I'm using equations from Paul Bourke's site to calculate the A, B, C and (-)D
coefficients in the plane equation,
#declare Point1 = <-1, 0.5, 1>;
#declare Point2 = <1, -0.25, 1>;
#declare Point3 = <0, -1, -1>;
cylinder {Point1, Point2 0.005 texture {pigment {Black}} }
cylinder {Point2, Point3 0.005 texture {pigment {Black}} }
cylinder {Point3, Point1 0.005 texture {pigment {Black}} }
// derive the plane equation
#declare A1 = Point1.y*(Point2.z-Point3.z) + Point2.y*(Point3.z-Point1.z) +
Point3.y*(Point1.z-Point2.z);
#declare B1 = Point1.z*(Point2.x-Point3.x) + Point2.z*(Point3.x-Point1.x) +
Point3.z*(Point1.x-Point2.x);
#declare C1 = Point1.x*(Point2.y-Point3.y) + Point2.x*(Point3.y-Point1.y) +
Point3.x*(Point1.y-Point2.y);
#declare D1 = -1*(Point1.x*(Point2.y*Point3.z-Point3.y*Point2.z) +
Point2.x*(Point3.y*Point1.z-Point1.y*Point3.z) +
Point3.x*(Point1.y*Point2.z-Point2.y*Point1.z));
#declare L = vlength (<A1, B1, C1>);
and after much fiddling, got the plane to pass through the three points, and the
p-vertex to be where I think it ought to be.
I'd like to figure out the length and direction of the normal vector of the
plane, and how to calculate the position of a point in the plane that is closest
to a point not in the plane (in this case, the p-vertex).
Likely there's a way to use POV-Ray's vector functions, and macros, with
rotations and translations, but I'd like to use a direct calculation - something
that would be straight out of analytical geometry.
(I looked through Friedrich Lohmueller's site and his analytical_g.inc file, but
I didn't find exactly what I was looking for - maybe I missed it)
[I am, admittedly, probably not thinking about this in the right way, and am
thus overcomplicating it for myself as usual]
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
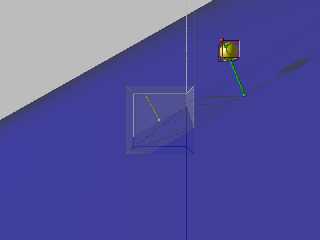
Whee!
Thanks to:
http://math.stackexchange.com/questions/723937/find-the-point-on-a-plane-3x-4y-z-1-that-is-closest-to-1-0-1
I worked out:
sphere {Pvertex 0.05 texture {pigment {Red} finish {specular 0.6}} }
// for plane A1*x+B1*y+C1*z=D1, what is closest point on plane to Pvertex?
// Normal vector to plane is <A1, B1, C1>
// closest point is some multiple of <A1, B1, C1> added to <Pvertex.x,
Pvertex.y, Pvertex.z>
// P = <Pvertex.x, Pvertex.y, Pvertex.z> + c*<A1, B1, C1> = <(Pvertex.x+c*A1),
(Pvertex.y+c*B1), (Pvertex.z+c*C1)>
// substitute this into the plane equation
// A1*(Pvertex.x+c*A1) + B1*(Pvertex.y+c*B1) + C1*(Pvertex.z+c*C1)> = D1
// A1*Pvertex.x+pow(A1,2)*c) + B1*Pvertex.y+pow(B1,2)*c) +
C1*Pvertex.z+pow(C1,2)*c) = D1
// (A1*Pvertex.x) + (B1*Pvertex.y) + (C1*Pvertex.z) + pow(A1,2)*c) +
pow(B1,2)*c) + pow(C1,2)*c) = D1
// pow(A1,2)*c) + pow(B1,2)*c) + pow(C1,2)*c) = D1 - ( (A1*Pvertex.x) +
(B1*Pvertex.y) + (C1*Pvertex.z) )
// c = D1 - ( (A1*Pvertex.x) + (B1*Pvertex.y) + (C1*Pvertex.z) ) / ( pow(A1,2) +
pow(B1,2) + pow(C1,2) )
#declare c = (D1 - ( (A1*Pvertex.x) + (B1*Pvertex.y) + (C1*Pvertex.z) ) ) / (
pow(A1,2) + pow(B1,2) + pow(C1,2) );
#debug concat ("c = ", str(c, 3, 3), "\n")
#declare P = Pvertex + (c*<A1, B1, C1>);
#debug concat ("Point on plane is: <", vstr(3, P, ", ", 3, 3), "> \n")
sphere {P 0.05 texture {pigment {Green} finish {specular 0.6}} }
cylinder {P, Pvertex, 0.025 texture {pigment {Green} finish {specular 0.6} }}
and this looks good. (finally)
Hopefully I'll have more time to work out some more of the code, optimize the
macros, and make a nice test scene.
Post a reply to this message
Attachments:
Download 'octanttest.png' (46 KB)
Preview of image 'octanttest.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Mike Horvath <mik### [at] gmail com> wrote:
> Are you using a perspective camera or orthographic?
I re-read this, and:
The camera for the native scene - using screen.inc, is perspective.
I have rear, side, and orthographic views that use an orthographic camera to
view the native perspective camera's frustum in the "meta-scene"
The side-rear view of the perspective frustum uses a perspective camera.
I've seen some references that define other frustrums (frusta?) that reshape the
perspective frustum into a rectangular solid ("clipping frustum") I suppose for
easier handling of the data.
That uses a matrix to transform the perspective frustum and object coordinates.
I don't see why a frustum for the native scene couldn't be orthographic - future
work. :) com> wrote:
> Are you using a perspective camera or orthographic?
I re-read this, and:
The camera for the native scene - using screen.inc, is perspective.
I have rear, side, and orthographic views that use an orthographic camera to
view the native perspective camera's frustum in the "meta-scene"
The side-rear view of the perspective frustum uses a perspective camera.
I've seen some references that define other frustrums (frusta?) that reshape the
perspective frustum into a rectangular solid ("clipping frustum") I suppose for
easier handling of the data.
That uses a matrix to transform the perspective frustum and object coordinates.
I don't see why a frustum for the native scene couldn't be orthographic - future
work. :)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 1/20/2017 10:08 AM, Bald Eagle wrote:
> Mike Horvath <mik### [at] gmail com> wrote:
>
>> Are you using a perspective camera or orthographic?
>
> I re-read this, and:
> The camera for the native scene - using screen.inc, is perspective.
> I have rear, side, and orthographic views that use an orthographic camera to
> view the native perspective camera's frustum in the "meta-scene"
> The side-rear view of the perspective frustum uses a perspective camera.
>
> I've seen some references that define other frustrums (frusta?) that reshape the
> perspective frustum into a rectangular solid ("clipping frustum") I suppose for
> easier handling of the data.
> That uses a matrix to transform the perspective frustum and object coordinates.
>
> I don't see why a frustum for the native scene couldn't be orthographic - future
> work. :)
>
>
>
I made a habit of using direction, location, up and right instead of
look_at, angle and sky. This makes such calculations a lot easier.
Mike com> wrote:
>
>> Are you using a perspective camera or orthographic?
>
> I re-read this, and:
> The camera for the native scene - using screen.inc, is perspective.
> I have rear, side, and orthographic views that use an orthographic camera to
> view the native perspective camera's frustum in the "meta-scene"
> The side-rear view of the perspective frustum uses a perspective camera.
>
> I've seen some references that define other frustrums (frusta?) that reshape the
> perspective frustum into a rectangular solid ("clipping frustum") I suppose for
> easier handling of the data.
> That uses a matrix to transform the perspective frustum and object coordinates.
>
> I don't see why a frustum for the native scene couldn't be orthographic - future
> work. :)
>
>
>
I made a habit of using direction, location, up and right instead of
look_at, angle and sky. This makes such calculations a lot easier.
Mike
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I was trying to work out a few things, and was using my code and that in
screen.inc as a guide, but of course nothing ever works out the way it's
supposed to.
Excel gives me wildly different results from what POV-Ray returns for the camera
view angle formula.
#declare Angle = 2*atan2d (0.5*CamR.x*Camera_Aspect_Ratio, CamD.z*Camera_Zoom);
I was hoping someone could run a quick check and confirm.
This certainly wouldn't be the first time Excel was just plain wrong.
Post a reply to this message
Attachments:
Download 'excel - angle.jpg' (24 KB)
Preview of image 'excel - angle.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 4/17/2017 7:47 AM, Bald Eagle wrote:
>
> I was trying to work out a few things, and was using my code and that in
> screen.inc as a guide, but of course nothing ever works out the way it's
> supposed to.
>
> Excel gives me wildly different results from what POV-Ray returns for the camera
> view angle formula.
>
> #declare Angle = 2*atan2d (0.5*CamR.x*Camera_Aspect_Ratio, CamD.z*Camera_Zoom);
>
> I was hoping someone could run a quick check and confirm.
>
> This certainly wouldn't be the first time Excel was just plain wrong.
>
Make sure you are using radians and degrees properly. You may have to
convert between the two.
Mike
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()