|
 |
Whee!
Thanks to:
http://math.stackexchange.com/questions/723937/find-the-point-on-a-plane-3x-4y-z-1-that-is-closest-to-1-0-1
I worked out:
sphere {Pvertex 0.05 texture {pigment {Red} finish {specular 0.6}} }
// for plane A1*x+B1*y+C1*z=D1, what is closest point on plane to Pvertex?
// Normal vector to plane is <A1, B1, C1>
// closest point is some multiple of <A1, B1, C1> added to <Pvertex.x,
Pvertex.y, Pvertex.z>
// P = <Pvertex.x, Pvertex.y, Pvertex.z> + c*<A1, B1, C1> = <(Pvertex.x+c*A1),
(Pvertex.y+c*B1), (Pvertex.z+c*C1)>
// substitute this into the plane equation
// A1*(Pvertex.x+c*A1) + B1*(Pvertex.y+c*B1) + C1*(Pvertex.z+c*C1)> = D1
// A1*Pvertex.x+pow(A1,2)*c) + B1*Pvertex.y+pow(B1,2)*c) +
C1*Pvertex.z+pow(C1,2)*c) = D1
// (A1*Pvertex.x) + (B1*Pvertex.y) + (C1*Pvertex.z) + pow(A1,2)*c) +
pow(B1,2)*c) + pow(C1,2)*c) = D1
// pow(A1,2)*c) + pow(B1,2)*c) + pow(C1,2)*c) = D1 - ( (A1*Pvertex.x) +
(B1*Pvertex.y) + (C1*Pvertex.z) )
// c = D1 - ( (A1*Pvertex.x) + (B1*Pvertex.y) + (C1*Pvertex.z) ) / ( pow(A1,2) +
pow(B1,2) + pow(C1,2) )
#declare c = (D1 - ( (A1*Pvertex.x) + (B1*Pvertex.y) + (C1*Pvertex.z) ) ) / (
pow(A1,2) + pow(B1,2) + pow(C1,2) );
#debug concat ("c = ", str(c, 3, 3), "\n")
#declare P = Pvertex + (c*<A1, B1, C1>);
#debug concat ("Point on plane is: <", vstr(3, P, ", ", 3, 3), "> \n")
sphere {P 0.05 texture {pigment {Green} finish {specular 0.6}} }
cylinder {P, Pvertex, 0.025 texture {pigment {Green} finish {specular 0.6} }}
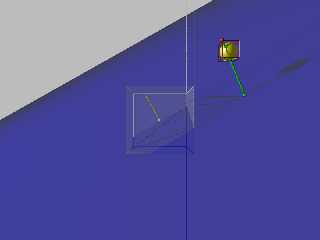
and this looks good. (finally)
Hopefully I'll have more time to work out some more of the code, optimize the
macros, and make a nice test scene.
Post a reply to this message
Attachments:
Download 'octanttest.png' (46 KB)
Preview of image 'octanttest.png'
|
 |




![]()