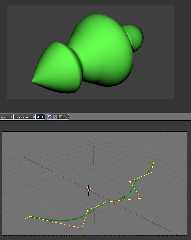
Hi!
I don't understand how sor is created?
The form doesn't correspond to a green curve. Not the curve, but control points
rotates.
Or it not NURBS?

nurbs, cubic, bubic. quadric, madric.
What is that? Oh, My God!
Why very much? There is bezier - clear and operated.
:)

Post a reply to this message

Attachments:
Download 'sor.jpg' (49 KB)

Preview of image 'sor.jpg'

Am 03.08.2015 um 19:33 schrieb LanuHum:
> Hi!
> I don't understand how sor is created?
> The form doesn't correspond to a green curve. Not the curve, but control points
> rotates.
> Or it not NURBS?
>
> nurbs, cubic, bubic. quadric, madric.
> What is that? Oh, My God!
> Why very much? There is bezier - clear and operated.
> :)

SOR is the surface of revolution of a piecewise defined 3rd-order 
(cubic) polynomial function (defined by a set of points on the curve) 
rotated about the x axis (and the resulting shape subsequently rotated 
so that its axis of rotational symmetry is mapped onto the y axis of 3D 
space); no splines involved.

To generate the surface of revolution of proper splines, there's the 
"lathe" keyword, which supports linear, quadratic and cubic splines (the 
latter with various different parameterizations based on the control 
points, including bezier splines).

POV-Ray doesn't support NURBS (non-uniform rational B-splines).

Post a reply to this message

clipka <ano### [at] anonymousorg> wrote:
> Am 03.08.2015 um 19:33 schrieb LanuHum:
> > Hi!
> > I don't understand how sor is created?
> > The form doesn't correspond to a green curve. Not the curve, but control points
> > rotates.
> > Or it not NURBS?
> >
> > nurbs, cubic, bubic. quadric, madric.
> > What is that? Oh, My God!
> > Why very much? There is bezier - clear and operated.
> > :)
>
> SOR is the surface of revolution of a piecewise defined 3rd-order
> (cubic) polynomial function (defined by a set of points on the curve)
> rotated about the x axis (and the resulting shape subsequently rotated
> so that its axis of rotational symmetry is mapped onto the y axis of 3D
> space); no splines involved.
>
> To generate the surface of revolution of proper splines, there's the
> "lathe" keyword, which supports linear, quadratic and cubic splines (the
> latter with various different parameterizations based on the control
> points, including bezier splines).
>
> POV-Ray doesn't support NURBS (non-uniform rational B-splines).

Thanks!
There is no support of nurbs, there is no support of bezier (an exception of
lathe and prism). Refusal of nurbs and bezier is a concept?
Badly. It strongly limits possibilities of data transmission from the Blender to
Povray.
I can't give animation, I can't give the arrays built along curves
Interestingly, what 3D - editors have no nurbs and bezier, but have cubic and
quadratic? I such didn't see.
If I wrote the AutodeskMaya2Povray exporter, I would meet the same problems?
:(

Post a reply to this message

-----BEGIN PGP SIGNED MESSAGE-----
Hash: SHA256

Le 04/08/2015 18:11, LanuHum a écrit :
> clipka <ano### [at] anonymousorg> wrote:
>> Am 03.08.2015 um 19:33 schrieb LanuHum:
>>> Hi! I don't understand how sor is created? The form doesn't
>>> correspond to a green curve. Not the curve, but control points 
>>> rotates. Or it not NURBS?
>>> 
>>> nurbs, cubic, bubic. quadric, madric. What is that? Oh, My
>>> God! Why very much? There is bezier - clear and operated. :)
>> 
>> SOR is the surface of revolution of a piecewise defined
>> 3rd-order (cubic) polynomial function (defined by a set of points
>> on the curve) rotated about the x axis (and the resulting shape
>> subsequently rotated so that its axis of rotational symmetry is
>> mapped onto the y axis of 3D space); no splines involved.
>> 
>> To generate the surface of revolution of proper splines, there's
>> the "lathe" keyword, which supports linear, quadratic and cubic
>> splines (the latter with various different parameterizations
>> based on the control points, including bezier splines).
>> 
>> POV-Ray doesn't support NURBS (non-uniform rational B-splines).
> 
> Thanks! There is no support of nurbs, there is no support of bezier
> (an exception of lathe and prism). Refusal of nurbs and bezier is a
> concept?

there is bicubic_patch.

http://povray.org/documentation/view/3.6.1/64/
http://wiki.povray.org/content/Reference:Bicubic_Patch
http://www.povray.org/documentation/view/3.6.1/290/

It's a Bezier patch.

> Badly. It strongly limits possibilities of data transmission from
> the Blender to Povray.

Most nurbs rendering transforms them in mesh anyway. (I recommend
mesh2 format for them).

It's not a concept (to refuse nurbs), it's just that solving the
intersection of a ray with a nurbs is not something that can be easily
solved mathematically (I would say: at once, without iterations or
approximation).

Now, if you can solve it (a nurbs, a ray, return the list of
intersection points) (as well as "a nurbs, a 3D point, return a
boolean for the point being inside the volume delimited by the nurbs),
without generating a mesh under the cover, it can be considered for
addition.

But beware, even bicubic_patch has a cheating method (type 1), as
solving pure (type 0) bezier is slow. (but memory effective)

> I can't give animation, I can't give the arrays built along curves 
> Interestingly, what 3D - editors have no nurbs and bezier, but have
> cubic and quadratic? I such didn't see. If I wrote the
> AutodeskMaya2Povray exporter, I would meet the same problems? :(
> 
> 

-----BEGIN PGP SIGNATURE-----
Version: GnuPG v2

iJwEAQEIAAYFAlXA/7IACgkQhKAm8mTpkW2JVQP9HQ0shhXRgdBYtEhitBbLuk9n
BnayAcsaqes3HvHXy3An+lyM1l8nHuzO3eFn2swXEUssqS3ZEqp/f8U/D7pNEoB4
xSkjqgj5VFXIpAdIMlM6ZoiCp2aPwbJHXj7HOBuYg0qshH4zelJAYJD5ndIYAWB0
w6o8viJdGO+aqjy4B20=
=0yi3
-----END PGP SIGNATURE-----

Post a reply to this message

Le_Forgeron <jgr### [at] freefr> wrote:

>
> there is bicubic_patch.
>
> http://povray.org/documentation/view/3.6.1/64/
> http://wiki.povray.org/content/Reference:Bicubic_Patch
> http://www.povray.org/documentation/view/3.6.1/290/
>
> It's a Bezier patch.
>
> > Badly. It strongly limits possibilities of data transmission from
> > the Blender to Povray.
>
> Most nurbs rendering transforms them in mesh anyway. (I recommend
> mesh2 format for them).
>
> It's not a concept (to refuse nurbs), it's just that solving the
> intersection of a ray with a nurbs is not something that can be easily
> solved mathematically (I would say: at once, without iterations or
> approximation).
>
> Now, if you can solve it (a nurbs, a ray, return the list of
> intersection points) (as well as "a nurbs, a 3D point, return a
> boolean for the point being inside the volume delimited by the nurbs),
> without generating a mesh under the cover, it can be considered for
> addition.
>
> But beware, even bicubic_patch has a cheating method (type 1), as
> solving pure (type 0) bezier is slow. (but memory effective)
>


Sorry!
No,no!
Before export I can convert all models in mesh.
No problem.
Problem with Constructive Solid Geometry
Not with all converted objects the blender correctly considers boolean.
Your(Povray) algorithms it is better!
Perhaps, it is connected with use by the Blender of quads.(Povray use tris)

And use while - problem.
I could set a cycle:
//Array =
//while (I < %s)
//translate Array%s[I]
but is compelled to calculate:
object {One translate<x1,y1,z1>}
...............................
object {Thousand  translate<x1000,y1000,z1000>}

And, for whom it is now easy? :):):)

The best wishes!

Post a reply to this message

Am 04.08.2015 um 18:11 schrieb LanuHum:

>> POV-Ray doesn't support NURBS (non-uniform rational B-splines).
>
> Thanks!
> There is no support of nurbs, there is no support of bezier (an exception of
> lathe and prism). Refusal of nurbs and bezier is a concept?

Bezier splines are just a special case of cubic splines, differing only 
in how the control points are translated into the coefficients for the 
polynomials used in the background.

Missing support for bezier in spline functions and sphere_sweep is just 
a matter of incomplete implementation, not of a philosophy.


One reason (the primary one in my book) for missing NURBS support has 
been the lack of affordable user interfaces to define NURBS surfaces and 
export the coefficients to a format suitable for POV-Ray. I wouldn't 
want to have to input NURBS coefficients directly to test such a 
feature, especially if I have no way of verifying the resulting shape.

I didn't know Blender supported NURBS surfaces. If it does, you could 
help by providing a very basic export function that just writes the 
coefficients to an array.

I only have a rudimentary understanding of the underlying math though, 
and there's other stuff high on my agenda at present, so don't hold your 
breath unless Jerome is willing to pick up the glove.

@Jerome: Even if the implementation would be similar to that of bicubic 
patch type 1, i.e. an internal translation to something mesh-like, so 
that in a sense the whole job could also be done by the exporter by 
generating a mesh2 object, I think a NURBS primitive would be beneficial 
in order to minimize file I/O in the workflow.


> If I wrote the AutodeskMaya2Povray exporter, I would meet the same problems?
> :(

I don't think so. I'm pretty sure Maya provides mechanisms for export 
filters to access mesh representations of NURBS surfaces rather than the 
NURBS coefficients themselves, so that would be an option.

Post a reply to this message

Le 04/08/2015 22:37, clipka a écrit :

>
> Missing support for bezier in spline functions and sphere_sweep is just
> a matter of incomplete implementation, not of a philosophy.
>

the spline in povray support 4 kinds: natural_spline, linear_spline, 
quadratic_spline and cubic_spline. The latter three matching the 
equations given in https://en.wikipedia.org/wiki/B%C3%A9zier_curve for
linear/quadratic/cubic Bézier curves.

sphere_sweep, in regard to Bézier, is limited to linear_spline and 
cubic_spline. (b_spline is a more general curve, which can or cannot be 
a Bèzier curve according to the spacing of the points)



>
> One reason (the primary one in my book) for missing NURBS support has
> been the lack of affordable user interfaces to define NURBS surfaces and
> export the coefficients to a format suitable for POV-Ray. I wouldn't
> want to have to input NURBS coefficients directly to test such a
> feature, especially if I have no way of verifying the resulting shape.

Yep, I even get tired of the syntax of poly{} object which was not 
reader & writer friendly at all. It took maybe twenty years to get the 
polynomial syntax (same object, just easier to handle).

>
> I didn't know Blender supported NURBS surfaces. If it does, you could
> help by providing a very basic export function that just writes the
> coefficients to an array.
>
> I only have a rudimentary understanding of the underlying math though,
> and there's other stuff high on my agenda at present, so don't hold your
> breath unless Jerome is willing to pick up the glove.
>
> @Jerome: Even if the implementation would be similar to that of bicubic
> patch type 1, i.e. an internal translation to something mesh-like, so
> that in a sense the whole job could also be done by the exporter by
> generating a mesh2 object, I think a NURBS primitive would be beneficial
> in order to minimize file I/O in the workflow.

I have some other items on my to-do-list (from a long time), and I might 
get stalled in a hen-egg situation: without an array of valid values for 
a nurbs, no incentive to parse and implement such object.
(hint: please provide an interesting nurbs, not just a sphere or a 
torus, something that is unique to nurbs)

If I get something right, the array would be a 2D rectangular array of 
4D values (3D positions of control points and weight).
A global tunning of the nurbs would be its order (2 or 4 ? can it be 
anything ? blender's doc states from 2 to 6), and wether each axis (of 
array) is endpoint or uniform (which i do not understand yet, seems tied 
to the knots setting, allowing only 2 knots vectors)

The dimensions of the array can be anything, each dimension being at 
least the order.


>
>
>> If I wrote the AutodeskMaya2Povray exporter, I would meet the same
>> problems?
>> :(
>
> I don't think so. I'm pretty sure Maya provides mechanisms for export
> filters to access mesh representations of NURBS surfaces rather than the
> NURBS coefficients themselves, so that would be an option.
>

Post a reply to this message

> >> If I wrote the AutodeskMaya2Povray exporter, I would meet the same
> >> problems?
> >> :(
> >
> > I don't think so. I'm pretty sure Maya provides mechanisms for export
> > filters to access mesh representations of NURBS surfaces rather than the
> > NURBS coefficients themselves, so that would be an option.
> >

Blender does support an "everything to triangle mesh" export as well, that's
what is implemented in the current exporter, but the idea of treating nurbs as
nurbs just as treating metaballs / blobs as such and any other pov primitive as
its native type like LanuHum is trying to do is much more powerfull to
allow always smooth renders.

Personnally I think the most polyvalent should be to support what JPAtch 0.3
used to support, a curve network converted to four sided bicubic patches, but
it's true native Blender Interface is better designed for NURBS at the moment.
all that would be needed to replace JPatch is a control point tag to "tie
together" several of the curves control points snapped in the same location. The
application of such a tool would bring a whole "market" to both Blender and POV.
the bicubics could also use a mesh with catmull clark subdiv modifier as
graphical input.

Post a reply to this message

I like the discussion.

clipka <ano### [at] anonymousorg> wrote:
>
> Bezier splines are just a special case of cubic splines, differing only
> in how the control points are translated into the coefficients for the
> polynomials used in the background.

So that's how it is. the bezier spline is just some polynomials in essence!!

Post a reply to this message

Why there was a question?
If I have the correct visualization of a curve in the editor, I can create
Constructive Solid Geometry.
On the picture green prism (bezier_spline) and red curve (bezier_spline).
If sphere_sweep, also as the prism, supported bezier_spline, it is possible to
write:
difference{
    object{prism}
    object(sphere_sweep}}

I can't make it.
I can't reel up a spiral on SOR.
I can SOR and sphere_sweep to model as nurbs, but to write down as cubic.
But, if to displace control points of a curve on Z, the geometry will be broken,
but control is absent also correction not to make.

Post a reply to this message

Attachments:
Download 'csg.jpg' (36 KB)

Preview of image 'csg.jpg'