 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Hi to the crowd,
I wonder a little bit about the threshold values of isosurfaces. From the docs:
The surface appears where the function value equals the threshold value.
I observe that the surface appears at values smaller than the threshold value if
it is not reached. To be more precise: I have a function yielding only 0 or 1
depending on the membership to a given set. 0 indicates membership, 1 not (1
minus the characteristic function of the set). Threshold values of 0.1, 0.2 and
0.9 all give the desired object. To my surprise 1.0 too, 1.1 gives the expected
unit sphere. Threshold 0.0 yields nothing.
May be a numeric issue at threshold 0.0 and 1.0.
What do I miss here?
Since I get my object I have no real problem, more a problem with understanding
the isosurface concepts.
Best regards,
Michael
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: Christian Froeschlin
Subject: Re: Nitpicking about isosurface threshold
Date: 9 Nov 2015 14:29:13
Message: <5640f409$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
> To be more precise: I have a function yielding
> only 0 or 1 depending on the membership to a given set.
I think the implicit assumption of the iso_surface is that
the set f(x) == threshold actually represents a 2d surface
and the numerical solver can creep up to that solution from
both sides using the 3d function gradient.
What you do seems more like a description of an "inside"
volume and you expect to render the surface of the volume.
I would not be surprised at unintuitive behavior here, I'm
more surprised you got a reasonable result at all :)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Christian Froeschlin <chr### [at] chrfr de> wrote:
> > To be more precise: I have a function yielding
> > only 0 or 1 depending on the membership to a given set.
>
> I think the implicit assumption of the iso_surface is that
> the set f(x) == threshold actually represents a 2d surface
> and the numerical solver can creep up to that solution from
> both sides using the 3d function gradient.
>
> What you do seems more like a description of an "inside"
> volume and you expect to render the surface of the volume.
> I would not be surprised at unintuitive behavior here, I'm
> more surprised you got a reasonable result at all :)
See Image at p.b.i de> wrote:
> > To be more precise: I have a function yielding
> > only 0 or 1 depending on the membership to a given set.
>
> I think the implicit assumption of the iso_surface is that
> the set f(x) == threshold actually represents a 2d surface
> and the numerical solver can creep up to that solution from
> both sides using the 3d function gradient.
>
> What you do seems more like a description of an "inside"
> volume and you expect to render the surface of the volume.
> I would not be surprised at unintuitive behavior here, I'm
> more surprised you got a reasonable result at all :)
See Image at p.b.i
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> I observe that the surface appears at values smaller than the threshold value if
> it is not reached. To be more precise: I have a function yielding only 0 or 1
Non-continuous functions like that are very tricky for the solver to
work with. Look up "mandelbulb distance function" and use something like
that rather than just a zero/one function. It will make the solver much
more efficient (ie better results in a shorter time).
> depending on the membership to a given set. 0 indicates membership, 1 not (1
> minus the characteristic function of the set). Threshold values of 0.1, 0.2 and
> 0.9 all give the desired object. To my surprise 1.0 too, 1.1 gives the expected
> unit sphere. Threshold 0.0 yields nothing.
>
> May be a numeric issue at threshold 0.0 and 1.0.
>
> What do I miss here?
The solver tries to find a small interval (the size of which depends on
"accuracy") where one side is below the interval and the other side is
above the interval. It does this by looking at the function value at the
first point on the ray, estimating how much further to look ahead based
on that value, then repeating, until it gets a satisfactory interval.
If your function is always one before the object, the solver must step
along very slowly taking many samples before it gets to a zero value.
Whether your "threshold" is 0.0001 or 0.9999 or anywhere in betweween
won't make any difference. Your function instantly flips from zero to
one, so any interval will always contain either all the values from zero
to one or none of them.
However if you use a distance field function, the function value might
be 100 at the first point, so the solver can take a huge step towards
the object. And then when it gets very close you'll get fractional
distances, so the solver can rapidly converge on an accurate interval
that contains the surface.
See below code from my GPU mandelbulb renderer that calculates the
distance function at a point, if it's any help:
float MB(vec3 pos)
{
pos.xyz = pos.xzy;
vec3 z = pos;
float dr = 1.0;
float r = 0.0;
for (int i = 0; i < 64 ; i++) {
r = length(z);
if (r>2.0)
break;
if(r==0.0)return 0.0;
// convert to polar coordinates
float theta = acos(z.z/r);
float phi = atan(z.y,z.x);
float zr = pow( r,N-1.0);
dr = zr*N*dr + 1.0;
// scale and rotate the point
theta = theta*N;
phi = phi*N;
// convert back to cartesian coordinates
z = zr*r*vec3(sin(theta)*cos(phi), sin(phi)*sin(theta), cos(theta));
z+=pos;
}
return 0.5*log(r)*r/dr;
}
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thank you very much. It helps indeed. First in understanding the isosurface and
second in understandig the mandelbulb computations. I wondered about a setting
by Tor Olav Kristensen in his code he gave here some years ago. Now I see that
this was an approach to estimate the distance to the mandelbulb, but different
from yours at first sight. But I must admit that my knowledge about stuff like
complex analysis and it extrapolation into 3-Space is a bit limited nowadays. If
I take his Mandelbulb function as a pigment function and compare it with yours,
differences are obvious. Since I like to play around with things, I will render
all three versions (Tor's, yours and my dichotomous one) and compare the
results.
Best regards,
Michael
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> Thank you very much. It helps indeed. First in understanding the isosurface and
> second in understandig the mandelbulb computations. I wondered about a setting
> by Tor Olav Kristensen in his code he gave here some years ago. Now I see that
> this was an approach to estimate the distance to the mandelbulb, but different
> from yours at first sight. But I must admit that my knowledge about stuff like
> complex analysis and it extrapolation into 3-Space is a bit limited nowadays.
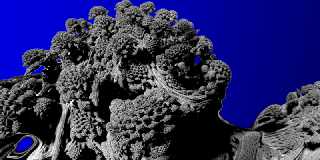
I don't pretend at all to have derived the distance equation, or even
understand how/why it works (or even have coded it correctly). But I did
get stuck in a similar situation to you when writing my GPU-based
isosurface renderer, and found the solution so thought I'd share. It
seems to work ok (see attached) so I stuck with it without
investigating/optimising further.
Post a reply to this message
Attachments:
Download 'download.png' (275 KB)
Preview of image 'download.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 10-11-2015 18:34, MichaelJF wrote:
> ... Since I like to play around with things, I will render
> all three versions (Tor's, yours and my dichotomous one) and compare the
> results.
>
Don't forget to show us :-)
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Looking at your very nice result and inspecting your code I think that you have
implemented the formula properly.
And I learned that one can post images to this group. Despite the fact that the
web front end states "You may not post attachments to this newsgroups". How did
you achieve this, Thunderbird?
Best regards,
Michael
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> On 10-11-2015 18:34, MichaelJF wrote:
> > ... Since I like to play around with things, I will render
> > all three versions (Tor's, yours and my dichotomous one) and compare the
> > results.
> >
>
> Don't forget to show us :-)
>
> --
> Thomas
I will post the three images ASAP. But they will be more technical and will
illustrate the resulting mandelbulb and a visualisation of the mandelbulb
function as a pigment function to understand the distance approximation better.
With the winner in render speed of my own small contest here, I will restart my
search for a nice place from May this year. I got stuck than since I found no
time to solve the riddles Tor Olav gave me with his code. But now I have a
better understanding, thanks Scott.
I imagine something like a cave where I can place some people exploring the
mandelbulb maybe sitting in a rowing boat, having a stalactite like texture to
the thing. And may be a falling drop. I hope I get this until mid of december.
My realisation of the mandelbulb is still a(n) (iso)surface;-)
Best regards,
Michael org> wrote:
> On 10-11-2015 18:34, MichaelJF wrote:
> > ... Since I like to play around with things, I will render
> > all three versions (Tor's, yours and my dichotomous one) and compare the
> > results.
> >
>
> Don't forget to show us :-)
>
> --
> Thomas
I will post the three images ASAP. But they will be more technical and will
illustrate the resulting mandelbulb and a visualisation of the mandelbulb
function as a pigment function to understand the distance approximation better.
With the winner in render speed of my own small contest here, I will restart my
search for a nice place from May this year. I got stuck than since I found no
time to solve the riddles Tor Olav gave me with his code. But now I have a
better understanding, thanks Scott.
I imagine something like a cave where I can place some people exploring the
mandelbulb maybe sitting in a rowing boat, having a stalactite like texture to
the thing. And may be a falling drop. I hope I get this until mid of december.
My realisation of the mandelbulb is still a(n) (iso)surface;-)
Best regards,
Michael
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"MichaelJF" <mi-### [at] t-online de> wrote:
> Looking at your very nice result and inspecting your code I think that you have
> implemented the formula properly.
>
> And I learned that one can post images to this group. Despite the fact that the
> web front end states "You may not post attachments to this newsgroups". How did
> you achieve this, Thunderbird?
Recalling my Usenet days, it's an honor system; and while news.povray.org is not
part of Usenet, the network protocol is identical. Newsreaders do not enforce
newsgroup policies. However, the Web interface is hosted on the server, and can
take enforcement options not available to newsreaders.
Perhaps Scott is unaware of the protocols of antiquity. Unless the newsgroup
has the word "binaries" in its name, one is expected not to post binaries to
that newsgroup, at the risk of being flamed or retromoderated. But flames are
rare in this community, and I can recall only two instances of retromoderation
in the 12 years I have been here.
On news.povray.org, there is an exception to this rule: povray.off-topic. Since
the Web interface permits binary attachments, I must assume that this exception
has official sanction. de> wrote:
> Looking at your very nice result and inspecting your code I think that you have
> implemented the formula properly.
>
> And I learned that one can post images to this group. Despite the fact that the
> web front end states "You may not post attachments to this newsgroups". How did
> you achieve this, Thunderbird?
Recalling my Usenet days, it's an honor system; and while news.povray.org is not
part of Usenet, the network protocol is identical. Newsreaders do not enforce
newsgroup policies. However, the Web interface is hosted on the server, and can
take enforcement options not available to newsreaders.
Perhaps Scott is unaware of the protocols of antiquity. Unless the newsgroup
has the word "binaries" in its name, one is expected not to post binaries to
that newsgroup, at the risk of being flamed or retromoderated. But flames are
rare in this community, and I can recall only two instances of retromoderation
in the 12 years I have been here.
On news.povray.org, there is an exception to this rule: povray.off-topic. Since
the Web interface permits binary attachments, I must assume that this exception
has official sanction.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()