 |
 |
|
 |
|
 |
|  |
|  |
|
 |
From: William F Pokorny
Subject: Suggest v4.0 f_bezier_2d_...() functions. (yuqk R19 v0.6.13.0)
Date: 22 Feb 2025 15:40:23
Message: <67ba3637$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
Adding the inbuilt functions: f_bezier_2d_linear()
f_bezier_2d_quadratic() f_bezier_2d_cubic() f_bezier_2d_quartic() and
f_bezier_2d_quintic() to the next yuqk release (R19).
The functions take and return single float packed 2d vectors in a
double's space for control points and return values. Calculations are at
double float accuracy internal to each functions code. The t parameter
is passed as a double.
The calculation and return mode settings:
0=<u,v> at t.
1=<u',v'> at t. (Tangent normalized)
2=<normal u,normal v> at t. ((1) rotated for normal)
3=<u',v'> at t. (Tangent / velocity)
4=<u'',v''> at t. (Acceleration / change in tangent)
5=<u''',v'''> at t. (Jerk / change in acceleration)
Attaching images showing all six calculation and return modes for
f_bezier_2d_cubic() f_bezier_2d_quartic() and f_bezier_2d_quintic().
Bill P.
Extra Detail
------------
The code approach settled upon will I believe easily map to 3D vectors
excepting the normal mode (2) calculations. Holding off though, I'd like
to play with this new 2d code for a while and, as inbuilt functions,
we'd end up working in a three, 21bit, float packed, reduced range for
the easy 3D adoption.
---
IIRC, Bald Eagle asked whether the derivatives weren't lower orders of
the Bezier curve itself. I currently believe the answer to be, yes, with
qualifications.
First, there are compensating factors for each derivative order based
upon the initial Bezier curve:
Quadratic derivative factors:
' --> 2
'' --> 2
''' --> DNA
Cubic derivative factors:
' --> 3
'' --> 6
''' --> 6
Quartic derivative factors:
' --> 4
'' --> 12
''' --> 24
Quintic derivative factors:
' --> 5
'' --> 20
''' --> 60
I used 1/(factors above) multipliers to better view the raw 1st, 2nd and
3rd derivative value curves(*) (modes 4,5 and 6) together. The
derivative value curves(*) tend to get much larger as the derivative
order increases.
Second, some algebra is required to come up with the new P' factors for
each derivative Bezier curve.
(*) - The curves are showing the entire sample set of values as spheres.
The strict sphere(t) curve may have folds where parts of the apparent
curve are getting retraced.
---
Post a reply to this message
Attachments:
Download 'f_bezier_2d_cubicstory.png' (18 KB)
Download 'f_bezier_2d_quarticstory.png' (31 KB)
Download 'f_bezier_2d_quinticstory.png' (30 KB)
Preview of image 'f_bezier_2d_cubicstory.png'
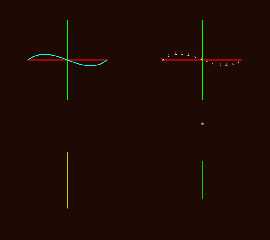
Preview of image 'f_bezier_2d_quarticstory.png'
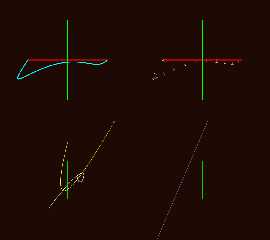
Preview of image 'f_bezier_2d_quinticstory.png'
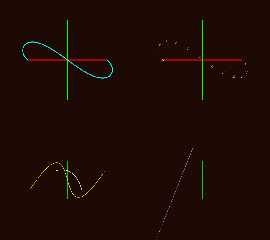
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> Adding the inbuilt functions: f_bezier_2d_linear()
> f_bezier_2d_quadratic() f_bezier_2d_cubic() f_bezier_2d_quartic() and
> f_bezier_2d_quintic() to the next yuqk release (R19).
>
> The functions take and return single float packed 2d vectors in a
> double's space for control points and return values. Calculations are at
> double float accuracy internal to each functions code. The t parameter
> is passed as a double.
Of use would also be a function that takes a t parameter and splits an extant
curve into 2 splines that are, over their combined lengths, equivalent to the
original Bezier curve.
I tested this in excel, and it works nicely.
#macro SplitBezier (P0, P1, P2, P3, t)
#local Q0 = P0 + t * (P1 - P0);
#local Q1 = P1 + t * (P2 - P1);
#local Q2 = P2 + t * (P3 - P2);
#local R0 = Q0 + t * (Q1 - Q0);
#local R1 = Q1 + t * (Q2 - Q1);
#local S = R0 + t * (R1 - R0);
// First segment: P0 to S
#declare Segment1 = array[4] {P0, Q0, R0, S};
// Second segment: S to P3
#declare Segment2 = array[4] {S, R1, Q2, P3};
Segment1, Segment2
#end
// Example usage
#declare P0 = <0, 0, 0>;
#declare P1 = <1, 2, 0>;
#declare P2 = <2, 2, 0>;
#declare P3 = <3, 0, 0>;
#declare t = 0.5;
#declare Segments = SplitBezier (P0, P1, P2, P3, t);
#declare Segment1 = Segments[0];
#declare Segment2 = Segments[1]; org> wrote:
> Adding the inbuilt functions: f_bezier_2d_linear()
> f_bezier_2d_quadratic() f_bezier_2d_cubic() f_bezier_2d_quartic() and
> f_bezier_2d_quintic() to the next yuqk release (R19).
>
> The functions take and return single float packed 2d vectors in a
> double's space for control points and return values. Calculations are at
> double float accuracy internal to each functions code. The t parameter
> is passed as a double.
Of use would also be a function that takes a t parameter and splits an extant
curve into 2 splines that are, over their combined lengths, equivalent to the
original Bezier curve.
I tested this in excel, and it works nicely.
#macro SplitBezier (P0, P1, P2, P3, t)
#local Q0 = P0 + t * (P1 - P0);
#local Q1 = P1 + t * (P2 - P1);
#local Q2 = P2 + t * (P3 - P2);
#local R0 = Q0 + t * (Q1 - Q0);
#local R1 = Q1 + t * (Q2 - Q1);
#local S = R0 + t * (R1 - R0);
// First segment: P0 to S
#declare Segment1 = array[4] {P0, Q0, R0, S};
// Second segment: S to P3
#declare Segment2 = array[4] {S, R1, Q2, P3};
Segment1, Segment2
#end
// Example usage
#declare P0 = <0, 0, 0>;
#declare P1 = <1, 2, 0>;
#declare P2 = <2, 2, 0>;
#declare P3 = <3, 0, 0>;
#declare t = 0.5;
#declare Segments = SplitBezier (P0, P1, P2, P3, t);
#declare Segment1 = Segments[0];
#declare Segment2 = Segments[1];
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
(and heck, while we're at it, why not just throw in 2 functions to degree
elevate and degree reduce a Bezier spline)
untested, not generalized (but I think you can see the pattern):
#macro DegreeElevateBezier(P0, P1, P2, P3)
#local Q0 = P0;
#local Q1 = (1/4)*P0 + (3/4)*P1;
#local Q2 = (1/2)*P1 + (1/2)*P2;
#local Q3 = (3/4)*P2 + (1/4)*P3;
#local Q4 = P3;
// Return the new control points
array[5] {Q0, Q1, Q2, Q3, Q4}
#end
#macro DegreeReduceBezier(Q0, Q1, Q2, Q3, Q4)
#local P0 = Q0;
#local P1 = (4/3)*Q1 - (1/3)*Q0;
#local P2 = (4/3)*Q3 - (1/3)*Q4;
#local P3 = Q4;
// Return the new control points
array[4] {P0, P1, P2, P3}
#end
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: William F Pokorny
Subject: Re: Suggest v4.0 f_bezier_2d_...() functions. (yuqk R19 v0.6.13.0)
Date: 27 Feb 2025 10:11:20
Message: <67c08098$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 2/27/25 09:21, Bald Eagle wrote:
> (and heck, while we're at it, why not just throw in 2 functions to degree
> elevate and degree reduce a Bezier spline)
:-) just...
Thanks for posting this code. I have no feel for it at the moment, but
would like to play. Longer term, I'll ponder the suggestions.
Initial reaction is I'm unsure how to nicely handle inputs and results
if made inbuilt today. And, I doubt whether these things really need to
be inbuilt functions? With the curves and derivatives themselves I
wanted to be able to use them within the VM at render time.
Maybe these could be shipped macros in a core include file...
Bill P.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> :-) just...
Yes, it's a sublimely phrased complement to "All you gotta do is..." ;)
> Thanks for posting this code. I have no feel for it at the moment, but
> would like to play. Longer term, I'll ponder the suggestions.
>
> Initial reaction is I'm unsure how to nicely handle inputs and results
> if made inbuilt today.
Not sure. I don't play under the hood as frequently as I probably should.
And I certainly don't write things to GO under the hood (yet).
All I can think of off-the-cuff is that the current matrix <> stores FOUR 3D
vectors. Perhaps that can be (ab)used.
> And, I doubt whether these things really need to
> be inbuilt functions? With the curves and derivatives themselves I
> wanted to be able to use them within the VM at render time.
All of this is with an eye of playing with the 48,000+ Bezier patch POV-Planet
and subdivisions. L.O.D and various Bezier-patch debugging functions could be
useful at render time to overlay wireframe grids, make curvature-dependent
textures, interpolate colors and textures - you name it. Can't do any of that
at render time with macros (unless we're doing the old, painful,
make-a-function-with-a-macro thing, which is also SLOOOOOOW)
> Maybe these could be shipped macros in a core include file...
They could be, but source-level methods integrated into the VM would be
something I think any good CG package would be expected to have.
Also, clipka was mentioning converting all of our text-rendering into prism {}
objects, and having an inbuilt Bezier library already implemented might be part
of making such a thing happen.
Plus, you know the POV-Ray type of experimenter - any and every feature will be
put to uses that none of us could ever expect.
Let's say that I wanted to take a sphere {} and make it into a QuadSphere made
out of Bezier patches. This would be nearly effortless if I took a circumscribed
cube and applied Bezier functions to the 4 vertices, and there were other spline
functions to solve for missing control points. (linear, spherical, etc.)
I'm just mentioning this at the present time because your mind is in this space,
you're coding that section of yuqk, and "the iron is hot".
Likely you'd have a blast doing all sorts of experiments once you had the tools
to play with.
- BW org> wrote:
> :-) just...
Yes, it's a sublimely phrased complement to "All you gotta do is..." ;)
> Thanks for posting this code. I have no feel for it at the moment, but
> would like to play. Longer term, I'll ponder the suggestions.
>
> Initial reaction is I'm unsure how to nicely handle inputs and results
> if made inbuilt today.
Not sure. I don't play under the hood as frequently as I probably should.
And I certainly don't write things to GO under the hood (yet).
All I can think of off-the-cuff is that the current matrix <> stores FOUR 3D
vectors. Perhaps that can be (ab)used.
> And, I doubt whether these things really need to
> be inbuilt functions? With the curves and derivatives themselves I
> wanted to be able to use them within the VM at render time.
All of this is with an eye of playing with the 48,000+ Bezier patch POV-Planet
and subdivisions. L.O.D and various Bezier-patch debugging functions could be
useful at render time to overlay wireframe grids, make curvature-dependent
textures, interpolate colors and textures - you name it. Can't do any of that
at render time with macros (unless we're doing the old, painful,
make-a-function-with-a-macro thing, which is also SLOOOOOOW)
> Maybe these could be shipped macros in a core include file...
They could be, but source-level methods integrated into the VM would be
something I think any good CG package would be expected to have.
Also, clipka was mentioning converting all of our text-rendering into prism {}
objects, and having an inbuilt Bezier library already implemented might be part
of making such a thing happen.
Plus, you know the POV-Ray type of experimenter - any and every feature will be
put to uses that none of us could ever expect.
Let's say that I wanted to take a sphere {} and make it into a QuadSphere made
out of Bezier patches. This would be nearly effortless if I took a circumscribed
cube and applied Bezier functions to the 4 vertices, and there were other spline
functions to solve for missing control points. (linear, spherical, etc.)
I'm just mentioning this at the present time because your mind is in this space,
you're coding that section of yuqk, and "the iron is hot".
Likely you'd have a blast doing all sorts of experiments once you had the tools
to play with.
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> Adding the inbuilt functions: f_bezier_2d_linear()
> f_bezier_2d_quadratic() f_bezier_2d_cubic() f_bezier_2d_quartic() and
> f_bezier_2d_quintic() to the next yuqk release (R19).
>
> The functions take and return single float packed 2d vectors in a
> double's space for control points and return values. Calculations are at
> double float accuracy internal to each functions code. The t parameter
> is passed as a double.
>
> The calculation and return mode settings:
> 0=<u,v> at t.
> 1=<u',v'> at t. (Tangent normalized)
> 2=<normal u,normal v> at t. ((1) rotated for normal)
> 3=<u',v'> at t. (Tangent / velocity)
> 4=<u'',v''> at t. (Acceleration / change in tangent)
> 5=<u''',v'''> at t. (Jerk / change in acceleration)
>
> Attaching images showing all six calculation and return modes for
> f_bezier_2d_cubic() f_bezier_2d_quartic() and f_bezier_2d_quintic().
>...
Hi Bill
That is Interesting.
But I can't figure out how to interpret the two bottom graphs in the
attached images.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k org> wrote:
> Adding the inbuilt functions: f_bezier_2d_linear()
> f_bezier_2d_quadratic() f_bezier_2d_cubic() f_bezier_2d_quartic() and
> f_bezier_2d_quintic() to the next yuqk release (R19).
>
> The functions take and return single float packed 2d vectors in a
> double's space for control points and return values. Calculations are at
> double float accuracy internal to each functions code. The t parameter
> is passed as a double.
>
> The calculation and return mode settings:
> 0=<u,v> at t.
> 1=<u',v'> at t. (Tangent normalized)
> 2=<normal u,normal v> at t. ((1) rotated for normal)
> 3=<u',v'> at t. (Tangent / velocity)
> 4=<u'',v''> at t. (Acceleration / change in tangent)
> 5=<u''',v'''> at t. (Jerk / change in acceleration)
>
> Attaching images showing all six calculation and return modes for
> f_bezier_2d_cubic() f_bezier_2d_quartic() and f_bezier_2d_quintic().
>...
Hi Bill
That is Interesting.
But I can't figure out how to interpret the two bottom graphs in the
attached images.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: William F Pokorny
Subject: Re: Suggest v4.0 f_bezier_2d_...() functions. (yuqk R19 v0.6.13.0)
Date: 1 Mar 2025 16:52:52
Message: <67c381b4$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 3/1/25 11:24, Tor Olav Kristensen wrote:
> But I can't figure out how to interpret the two bottom graphs in the
> attached images.
I'm uncomfortable with how to represent the derivative graphs where they
turn completely or partially constant.
I needed to normalize returned u,v values to get the scales into
somewhat similar ranges for viewing - which corrupts them some too. The
derivative plots sometimes end up being sets of values more the any sort
of curve. We are looking at spheres at u,v locations.
On the lower left in white are the first derivative x,y points as
spheres. The yellow is the second derivative and here all the values
overlap the y axis.
On the right the purple spheres are the completely constant x,y second
derivative values returned. The spheres are all at the same location.
---
While working on the code for these inbuilt functions I set up some
plots using isosurfaces to graph where I took care to align the 'x' and
't' values while evenly spacing the control points. For me these plots
make more intuitive sense because I can plot v vs u. Let me see if I
still have some of those around...
Found one. Quadratic, Cubic on the top. Quartic, Quintic on the bottom.
The cyan is the Bezier curve itself. The slate blue is the normalized
derivative. The white the second derivative - where it crosses the u
axis at y==zero we have the inflection points of the first derivative curve.
Aside: Thanks for your post on Jean Gallier's online material. I made a
note of it. I have a hard copy of that curves and surfaces book. I found
it, less immediately useful than I'd hoped - because I'm a maths hack. :-)
Bill P.
Post a reply to this message
Attachments:
Download 'f_bezier_2d_n2n3n4_and_n5.png' (93 KB)
Preview of image 'f_bezier_2d_n2n3n4_and_n5.png'
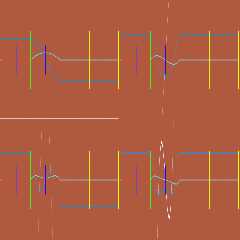
|
 |
|  |
|  |
|
 |
From: William F Pokorny
Subject: Re: Suggest v4.0 f_bezier_2d_...() functions. (yuqk R19 v0.6.13.0)
Date: 2 Mar 2025 12:13:49
Message: <67c491cd$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 3/1/25 16:52, William F Pokorny wrote:
> On the right the purple spheres are the completely constant x,y second
> derivative...
Should've read: ..."u,v third derivative"...
I also wasn't consistent in using u,v rather than x,y throughout.
Argh, the writing I inflict on you all :-(.
Bill P.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()