Howdy everyone.  Boy it's been a LONG time!

But, I'm back!  At least for a little while.


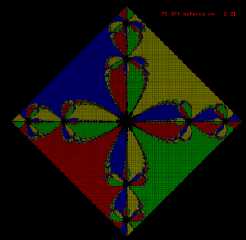
Fractal based off of roots of an equation in the complex plane.  Each color
represents the root of attraction using Newton's method from a particular
starting point.  This is just the beginning, and I may have some questions
to ask as to the best way to neat-ify this type of image (made up purely of
a crapload of spheres).

http://stuff.loneshepherd.com/frac/mine4.gif  for the big version (360kb).

--


Mike Metheny

"He that breaks a thing to find out what it is has left the path of wisdom."

Post a reply to this message

Attachments:
Download 'mine4s.gif' (26 KB)

Preview of image 'mine4s.gif'

Mike Metheny wrote:
> 
> Howdy everyone.  Boy it's been a LONG time!
> 
> But, I'm back!  At least for a little while.
> 
> Fractal based off of roots of an equation in the complex plane.  Each color
> represents the root of attraction using Newton's method from a particular
> starting point.  This is just the beginning, and I may have some questions
> to ask as to the best way to neat-ify this type of image (made up purely of
> a crapload of spheres).

How do you use Newton's method with complex numbers?  That's the
tangent-line-x-intercept method IIRC, right?  I saw this same pic in the
book Chaos.

-- 
David Fontaine  <dav### [at] faricynet>  ICQ 55354965
My raytracing gallery:  http://davidf.faricy.net/

Post a reply to this message

Yep; that particular fractal layout was my reproduction of the cover of the
book "Numerical Analysis" by kincaid and cheney.  You can check out my
ongoing progress here:

http://www.loneshepherd.com/frac.html

Newton's method works in the complex plane exactly as it does on the real
axis; you just start your iteration with a complex number.

that particular eqn shown is z^4 + 4 on a [-2,2] interval.  It is
diamondacized so as to look cool (and because the upper corners of the
square part don't really contain anything exciting).

--


Mike Metheny

"He that breaks a thing to find out what it is has left the path of wisdom."

Post a reply to this message

Mike Metheny wrote:
> 
> Newton's method works in the complex plane exactly as it does on the real
> axis; you just start your iteration with a complex number.

I don't get it.  Wouldn't a 2d function (real+imaginary) have a
tangent-plane, not a tangent line?  And the intersection of that with
another plane is a line.  You'd want a point...  explain this to me.

-- 
David Fontaine  <dav### [at] faricynet>  ICQ 55354965
My raytracing gallery:  http://davidf.faricy.net/

Post a reply to this message

<<
I don't get it.  Wouldn't a 2d function (real+imaginary) have a
tangent-plane, not a tangent line?  And the intersection of that with
another plane is a line.  You'd want a point...  explain this to me.
>>

Okay; take the function that generates this image:

we want the roots of z^4 + 4.  so we need z^4 = -4

it's to the 4th power, so it has 4 roots.  we can directly solve for the
roots by doing (-4)^(1/4) and using the formula:

r^(1/n) * [cos( (theta + 2*pi*k) / n ) + i * sin( (theta + 2*pi*k) / n ) ]

where r is the radius of the complex number (here we're using -4 as our
complex number; it has no imaginary part so the radius is just 4) and theta
is the angle from the +x axis around to that point in the complex plane( a
point at 1 + i would have a theta of pi/4, for our example, our point -4 +
0i we have a theta of pi).

n is the number of roots, 4, and k ranges from 0 to n-1.  this gives us all


You're right in that newton's method is a slope method, but don't get too
caught up on the visualizations.  what we do with NM is guess a root, and
then subtract from that guess the function evaluated at that guess divided
by the derivative of the function evaluated at that guess, or

z - f(z) / f'(z) gives us our new guess.

this will work just fine to find complex roots.  lets say we guess 2 + i as
a root, for instance.

f(z) = z^4 + 4 = (2+i)^4 + 4 = -3 + 24i
f'(z) = 4*z^3 = 8 + 4i

(2+i) - (-3+24i)/(8+4i) = 1.1 - 1.55i

Making this our new guess, our next iteration gives us approximately 0.965 -
1.20i, our third iteration gives 0.968 - 1.02i, etc etc.  You see that we
are converging to one of the roots, namely 1 - i.

However, if you were to start with something like 2 as your guess, your new
approximation would diverge; and bounce around all over the place like crazy
with this function; since there are no real roots.  So NM works just fine to
find complex roots, but you have to start with a complex number in the first
place, otherwise you will not converge to a complex number.

I think you're just getting a bit hung up on the graphical description of
newton's method (pick a point, draw a tangent line from that point to the
axis, use this as your new x value, and repeat).

--


Mike Metheny

"He that breaks a thing to find out what it is has left the path of wisdom."

Post a reply to this message

"Mike Metheny" <lon### [at] vtedu> wrote:

><<
>I don't get it.  Wouldn't a 2d function (real+imaginary) have a
>tangent-plane, not a tangent line?  And the intersection of that with
>another plane is a line.  You'd want a point...  explain this to me.
>>>
>
>Okay; take the function that generates this image:
>
>we want the roots of z^4 + 4.  so we need z^4 = -4
>
>it's to the 4th power, so it has 4 roots.  we can directly solve for the
>roots by doing (-4)^(1/4) and using the formula:
>
>r^(1/n) * [cos( (theta + 2*pi*k) / n ) + i * sin( (theta + 2*pi*k) / n ) ]
>
>where r is the radius of the complex number (here we're using -4 as our
>complex number; it has no imaginary part so the radius is just 4) and theta
>is the angle from the +x axis around to that point in the complex plane( a
>point at 1 + i would have a theta of pi/4, for our example, our point -4 +
>0i we have a theta of pi).
>
>n is the number of roots, 4, and k ranges from 0 to n-1.  this gives us all

>
>You're right in that newton's method is a slope method, but don't get too
>caught up on the visualizations.  what we do with NM is guess a root, and
>then subtract from that guess the function evaluated at that guess divided
>by the derivative of the function evaluated at that guess, or
>
>z - f(z) / f'(z) gives us our new guess.
>
>this will work just fine to find complex roots.  lets say we guess 2 + i as
>a root, for instance.
>
>f(z) = z^4 + 4 = (2+i)^4 + 4 = -3 + 24i
>f'(z) = 4*z^3 = 8 + 4i
>
>(2+i) - (-3+24i)/(8+4i) = 1.1 - 1.55i
>
>Making this our new guess, our next iteration gives us approximately 0.965 -
>1.20i, our third iteration gives 0.968 - 1.02i, etc etc.  You see that we
>are converging to one of the roots, namely 1 - i.
>
>However, if you were to start with something like 2 as your guess, your new
>approximation would diverge; and bounce around all over the place like crazy
>with this function; since there are no real roots.  So NM works just fine to
>find complex roots, but you have to start with a complex number in the first
>place, otherwise you will not converge to a complex number.
>
>I think you're just getting a bit hung up on the graphical description of
>newton's method (pick a point, draw a tangent line from that point to the
>axis, use this as your new x value, and repeat).

Uh...yer like smart and stuff...  jeez my head hurts just looking at this.
:)

Oldstench................

Post a reply to this message

Mike Metheny wrote:
> 
> z - f(z) / f'(z) gives us our new guess.

Of course!  Well, I've only had a year of calculus.  It makes sense now,
thanks.

I'm sure the visulaization problem had something to do with complex
number plane not being a Euclidean geometry or something like that. 
Like that whole "complex time" crap in the Stephen Hawking book...  I
suppose I'll learn all this after ten years of post-graduate set theory.
;)

-- 
David Fontaine  <dav### [at] faricynet>  ICQ 55354965
My raytracing gallery:  http://davidf.faricy.net/

Post a reply to this message