 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
have been experimenting with all manner of what can be done with a simple
pigment {function {}}
statement.
I currently have a list of 155 different patterns, including simple y = f(x)
style functions, implicit equations (some combination of x&y) = (some other
combination of x&y), and even some parametric polar equations and what I believe
are parametric Cartesian equations.
Hammering out that many equations one after the other and using different
methods to visualize the "raw" results has allowed me to learn some new things
and gain valuable insights into how best achieve a good, aesthetically pleasing
result, and why some patterns might be difficult to implement in the absence of
various "tricks".
At this junction, I would like to thank everyone in the POV-Ray community, and
especially Tor Olav Kristensen, Sam Benge, jr, William Pokorny, Jerome Grimbert,
as well as the vast Shadertoy community - most notably Inigo Quilez, Martijn
Steinrucken, and FabriceNeyret2, for inspiring me, and setting me on the path of
discovery with regard to using functions to make amazing patterns.
With that, I'll just leave here a most amazing Greek frieze pattern, produced by
an astonishingly small amount of code, adapted to SDL from a shader by
FabriceNeyret2.
While this is probably one of the most complex patterns I've adapted, simply due
to some specialized and highly technical methods that make its visibility even
possible, I'd love to see people experimenting with simple equations to produce
interesting patterns that we can build a library of.
After progressively trimming down the amount of code I need to make a simple
grid on a plane, I'd love to see such patterns code-golfed down to the bare
minimum, and then parameterized to increase their variation and versatility.
Happy New Year, everyone.
- Bald Eagle
Post a reply to this message
Attachments:
Download 'mathpatterns1.png' (973 KB)
Preview of image 'mathpatterns1.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 05/01/2024 om 22:50 schreef Bald Eagle:
>
> [snip]
>
> While this is probably one of the most complex patterns I've adapted, simply due
> to some specialized and highly technical methods that make its visibility even
> possible, I'd love to see people experimenting with simple equations to produce
> interesting patterns that we can build a library of.
>
> After progressively trimming down the amount of code I need to make a simple
> grid on a plane, I'd love to see such patterns code-golfed down to the bare
> minimum, and then parameterized to increase their variation and versatility.
>
> Happy New Year, everyone.
>
First of all: a Happy (and POV-Productive) New Year.
I am literally speechless. You did an awesome bit of work and I wouldn't
know where to begin, especially as my mathematical skills are rather
rudimentary. Are you going to provide us with some basic guide lines on
how to start such experimentation? I guess that would be needed for
several of us, setting us on our way.
Thanks indeed for your - and all those others - great work!
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
>
Excellent!!
I always had/have hoped that at some time the function language would grow a bit
in the direction of shaders by making more/all internal data available to
functions. Colour and normals are obvious, but just think of having also data on
radiosity, photons and what else there is inside POV-Ray that can be (ab)used.
These internal data do not even have to have any relation to textures or
objects. It's up to the artist to do something with them.
Photon data based displacement mapping for re-modeling meshes ...
A texture dependent on the number of times the light ray bounced before
intersection. Or normals based on the total length of a ray.
"Geluk in' tuk" (good luck in your pocket) for 2024,
ingo net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
>
Excellent!!
I always had/have hoped that at some time the function language would grow a bit
in the direction of shaders by making more/all internal data available to
functions. Colour and normals are obvious, but just think of having also data on
radiosity, photons and what else there is inside POV-Ray that can be (ab)used.
These internal data do not even have to have any relation to textures or
objects. It's up to the artist to do something with them.
Photon data based displacement mapping for re-modeling meshes ...
A texture dependent on the number of times the light ray bounced before
intersection. Or normals based on the total length of a ray.
"Geluk in' tuk" (good luck in your pocket) for 2024,
ingo
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> First of all: a Happy (and POV-Productive) New Year.
Thanks Thomas, I hope to see some more excellent landscapes, textures, or even
just doodles with no particular point behind them.
> I am literally speechless.
Ha! So was I. :D The shader is literally only 6 lines of code.
It still took me a fair amount of time to grope in the pitch black towards a
solution.
The funny thing is, earlier in the day I had been struggling (once more) to make
a simple spiral pattern, and here is a spiral, evenly divided into cells by
spiral arc-length, with different animated spirals in each cell!
I was also really happy that the solution relied on using the fwidth function,
as that lit a fire under my lazy butt to actually implement that in SDL as well.
So now I think I actually have all of the tools to push forward on coding the
knots in the wood texture, along with the spiral interpolation thing... all
because I was doing something completely unrelated, and juts serendipitously
stumbled upon a shader that was linked from a page I found through an image
search.
> You did an awesome bit of work and I wouldn't
> know where to begin, especially as my mathematical skills are rather
> rudimentary.
You, and Kenneth, and jr have all expressed as much, but I will tell you that
it's less about "knowing" the math, than simply acquiring a "feel" for it - a
sense of what types of things are related to what you're trying to accomplish,
or recognizing what terms in an equation are likely to be related to what parts
of the graph's shape.
Playing with an existing equation can rapidly sort all of that out, even if
initially it's all as opaque as obsidian.
> Are you going to provide us with some basic guide lines on
> how to start such experimentation? I guess that would be needed for
> several of us, setting us on our way.
Yes, I started summarizing the things I discovered in a comment section of my
patterns scene, and I'm hoping at some point to make further progress on a
function monograph that I started, specifically with jr and Kenneth in mind.
I think there are several things that have prevented me from successfully coding
some of the patterns that I've tried to reproduce in the past - and that makes
me think that I was probably tantalizingly close, but either I fell into the
trap of convincing myself that "it just couldn't be done", or there were some
finer points of how to visualize what was going on that I was missing.
I'm sure I must have threw away a few equations here & there in this last coding
frenzy, simply because I forgot to subtract the whole thing from y, and so it
just looked like a lot of random static.
I'm finishing up an extended family visit, and have an event to attend later
this evening, but after I get everything settled after that, I ought to have
some uninterrupted hours to devote to doing some more experiments, writing some
educational code, and hopefully finding ways to create some example scenes and
explain things clearly enough so that it's easy enough to follow.
It would actually help a lot to just write out a big list of things that you've
always wondered about, want to do, tried but were confused by, or any other
curiosities and speculations - so that I have a target to aim for.
It's not so much that "you don't know math / were never taught it / don't have
the skills", but WHY certain things are confusing or unknown to you.
Then I can think about what needs explaining, how best to explain it, and what
examples I can code to best illustrate the concepts. And to be honest, I'm
still at the stage where I don't clearly understand exactly how half of the
stuff I code actually works - so I may do a lot of hand-waving until some of the
smarter people (TOK, Jerome, WFP, Ingo) chime in with explanations or links that
lead me by the nose hairs to enlightenment.
All the best,
- BW org> wrote:
> First of all: a Happy (and POV-Productive) New Year.
Thanks Thomas, I hope to see some more excellent landscapes, textures, or even
just doodles with no particular point behind them.
> I am literally speechless.
Ha! So was I. :D The shader is literally only 6 lines of code.
It still took me a fair amount of time to grope in the pitch black towards a
solution.
The funny thing is, earlier in the day I had been struggling (once more) to make
a simple spiral pattern, and here is a spiral, evenly divided into cells by
spiral arc-length, with different animated spirals in each cell!
I was also really happy that the solution relied on using the fwidth function,
as that lit a fire under my lazy butt to actually implement that in SDL as well.
So now I think I actually have all of the tools to push forward on coding the
knots in the wood texture, along with the spiral interpolation thing... all
because I was doing something completely unrelated, and juts serendipitously
stumbled upon a shader that was linked from a page I found through an image
search.
> You did an awesome bit of work and I wouldn't
> know where to begin, especially as my mathematical skills are rather
> rudimentary.
You, and Kenneth, and jr have all expressed as much, but I will tell you that
it's less about "knowing" the math, than simply acquiring a "feel" for it - a
sense of what types of things are related to what you're trying to accomplish,
or recognizing what terms in an equation are likely to be related to what parts
of the graph's shape.
Playing with an existing equation can rapidly sort all of that out, even if
initially it's all as opaque as obsidian.
> Are you going to provide us with some basic guide lines on
> how to start such experimentation? I guess that would be needed for
> several of us, setting us on our way.
Yes, I started summarizing the things I discovered in a comment section of my
patterns scene, and I'm hoping at some point to make further progress on a
function monograph that I started, specifically with jr and Kenneth in mind.
I think there are several things that have prevented me from successfully coding
some of the patterns that I've tried to reproduce in the past - and that makes
me think that I was probably tantalizingly close, but either I fell into the
trap of convincing myself that "it just couldn't be done", or there were some
finer points of how to visualize what was going on that I was missing.
I'm sure I must have threw away a few equations here & there in this last coding
frenzy, simply because I forgot to subtract the whole thing from y, and so it
just looked like a lot of random static.
I'm finishing up an extended family visit, and have an event to attend later
this evening, but after I get everything settled after that, I ought to have
some uninterrupted hours to devote to doing some more experiments, writing some
educational code, and hopefully finding ways to create some example scenes and
explain things clearly enough so that it's easy enough to follow.
It would actually help a lot to just write out a big list of things that you've
always wondered about, want to do, tried but were confused by, or any other
curiosities and speculations - so that I have a target to aim for.
It's not so much that "you don't know math / were never taught it / don't have
the skills", but WHY certain things are confusing or unknown to you.
Then I can think about what needs explaining, how best to explain it, and what
examples I can code to best illustrate the concepts. And to be honest, I'm
still at the stage where I don't clearly understand exactly how half of the
stuff I code actually works - so I may do a lot of hand-waving until some of the
smarter people (TOK, Jerome, WFP, Ingo) chime in with explanations or links that
lead me by the nose hairs to enlightenment.
All the best,
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>
> With that, I'll just leave here a most amazing Greek frieze pattern, produced by
> an astonishingly small amount of code, adapted to SDL from a shader by
> FabriceNeyret2.
>
That is spectacularly beautiful! I'm dumbfounded, and amazed that your got
POV-ray to render such a fantastical pattern.
Keep at it, by all means; I can't wait to see what else you come up with. net> wrote:
>
> With that, I'll just leave here a most amazing Greek frieze pattern, produced by
> an astonishingly small amount of code, adapted to SDL from a shader by
> FabriceNeyret2.
>
That is spectacularly beautiful! I'm dumbfounded, and amazed that your got
POV-ray to render such a fantastical pattern.
Keep at it, by all means; I can't wait to see what else you come up with.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> With that, I'll just leave here a most amazing Greek frieze pattern, produced by
> an astonishingly small amount of code, adapted to SDL from a shader by
> FabriceNeyret2.
>...
Very nice. Well done!
I'm glad to see that you are advancing your math and coding skills Bill.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
>...
> With that, I'll just leave here a most amazing Greek frieze pattern, produced by
> an astonishingly small amount of code, adapted to SDL from a shader by
> FabriceNeyret2.
>...
Very nice. Well done!
I'm glad to see that you are advancing your math and coding skills Bill.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> Very nice. Well done!
>
> I'm glad to see that you are advancing your math and coding skills Bill.
Well, I'm moving forward bit by bit, but all the credit for that pattern
definitely goes to the author.
There's a function or two that I need to puzzle out to understand what they do
and how they are so essential to creating the pattern.
Just as a reminder to myself, I may have to branch out into the 3rd dimension to
see if I can work some of the same "magic" with media density by incorporating
z.
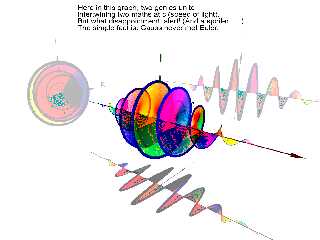
However, along those lines, I was admiring another nice little piece of work
that I stumbled across, and it prompted me to work out the gory details of
Euler's formula, Taylor series, and all of that "e to the power of" stuff that
seems to creep into all manner of interesting topics.
I edited the poem a bit, but shamelessly stole the idea (even though I had to
painfully work out the implementation from first principles). I didn't realize
I'd need about 20 terms in the Taylor series to get a good enough approximation.
:O
Enjoy the eye and mind candy.
- BW com> wrote:
> Very nice. Well done!
>
> I'm glad to see that you are advancing your math and coding skills Bill.
Well, I'm moving forward bit by bit, but all the credit for that pattern
definitely goes to the author.
There's a function or two that I need to puzzle out to understand what they do
and how they are so essential to creating the pattern.
Just as a reminder to myself, I may have to branch out into the 3rd dimension to
see if I can work some of the same "magic" with media density by incorporating
z.
However, along those lines, I was admiring another nice little piece of work
that I stumbled across, and it prompted me to work out the gory details of
Euler's formula, Taylor series, and all of that "e to the power of" stuff that
seems to creep into all manner of interesting topics.
I edited the poem a bit, but shamelessly stole the idea (even though I had to
painfully work out the implementation from first principles). I didn't realize
I'd need about 20 terms in the Taylor series to get a good enough approximation.
:O
Enjoy the eye and mind candy.
- BW
Post a reply to this message
Attachments:
Download 'eulergaussspiral.png' (218 KB)
Preview of image 'eulergaussspiral.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 09/01/2024 om 21:07 schreef Bald Eagle:
> Enjoy the eye and mind candy.
>
Oh LOL! Well done :-)
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
>
> I currently have a list of 155 different patterns, including simple y = f(x)
> style functions, implicit equations (some combination of x&y) = (some other
> combination of x&y), and even some parametric polar equations and what I believe
> are parametric Cartesian equations.
>
> Hammering out that many equations one after the other and using different
> methods to visualize the "raw" results has allowed me to learn some new things
> and gain valuable insights into how best achieve a good, aesthetically pleasing
> result, and why some patterns might be difficult to implement in the absence of
> various "tricks".
>
> At this junction, I would like to thank everyone in the POV-Ray community, and
> especially Tor Olav Kristensen, Sam Benge, jr, William Pokorny, Jerome Grimbert,
> as well as the vast Shadertoy community - most notably Inigo Quilez, Martijn
> Steinrucken, and FabriceNeyret2, for inspiring me, and setting me on the path of
> discovery with regard to using functions to make amazing patterns.
>
> With that, I'll just leave here a most amazing Greek frieze pattern, produced by
> an astonishingly small amount of code, adapted to SDL from a shader by
> FabriceNeyret2.
>
> While this is probably one of the most complex patterns I've adapted, simply due
> to some specialized and highly technical methods that make its visibility even
> possible, I'd love to see people experimenting with simple equations to produce
> interesting patterns that we can build a library of.
>
> After progressively trimming down the amount of code I need to make a simple
> grid on a plane, I'd love to see such patterns code-golfed down to the bare
> minimum, and then parameterized to increase their variation and versatility.
>
> Happy New Year, everyone.
>
> - Bald Eagle
Wow, this one looks not easy and beautiful. net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
>
> I currently have a list of 155 different patterns, including simple y = f(x)
> style functions, implicit equations (some combination of x&y) = (some other
> combination of x&y), and even some parametric polar equations and what I believe
> are parametric Cartesian equations.
>
> Hammering out that many equations one after the other and using different
> methods to visualize the "raw" results has allowed me to learn some new things
> and gain valuable insights into how best achieve a good, aesthetically pleasing
> result, and why some patterns might be difficult to implement in the absence of
> various "tricks".
>
> At this junction, I would like to thank everyone in the POV-Ray community, and
> especially Tor Olav Kristensen, Sam Benge, jr, William Pokorny, Jerome Grimbert,
> as well as the vast Shadertoy community - most notably Inigo Quilez, Martijn
> Steinrucken, and FabriceNeyret2, for inspiring me, and setting me on the path of
> discovery with regard to using functions to make amazing patterns.
>
> With that, I'll just leave here a most amazing Greek frieze pattern, produced by
> an astonishingly small amount of code, adapted to SDL from a shader by
> FabriceNeyret2.
>
> While this is probably one of the most complex patterns I've adapted, simply due
> to some specialized and highly technical methods that make its visibility even
> possible, I'd love to see people experimenting with simple equations to produce
> interesting patterns that we can build a library of.
>
> After progressively trimming down the amount of code I need to make a simple
> grid on a plane, I'd love to see such patterns code-golfed down to the bare
> minimum, and then parameterized to increase their variation and versatility.
>
> Happy New Year, everyone.
>
> - Bald Eagle
Wow, this one looks not easy and beautiful.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
(Still experimenting and struggling with various aspects of getting patterns
from other platforms to play well with SDL.)
> Hammering out that many equations one after the other ... has allowed me to learn
some new things and gain valuable i
nsights ...
OK, just to list the ones that I've written down so far:
(Questions, comments, and constructive criticism welcome as always)
Important tips to generate quality patterns from equations
----------------------------------------------------------
Be very careful with the use of parentheses - especially when + or - is in an
equation. Group terms.
You may want to declare different parts of a complex equation as separate
functions, then combine them in the final function
Use fmod instead of mod to get a regular repetition of a pattern across the
origin
HOWEVER, sometimes using mod in certain functions gives a better (more
expected) result - so try both
Use Mike Williams' "shell" trick for isosurfaces to give an infinitely thin line
a visible thickness
Change the line thickness to give definition to patterns that may not show up
with smaller values.
Some equations don't cross the zero/integer/mod threshold often enough to show
finer details. Multiply the
WHOLE equation (use parentheses) by a factor to increase the number of
lines/levels.
Zoom in or out to see pattern attributes that may not be visible or clearly
rendered.
If you're graphing y as a function of x, then you must write it in the form of:
function {y - formula} since when y=formula, the value is 0
If you're graphing a 2-argument function of both x and y, then you must write it
in the form of: function {(x - x_formula) + (y - y_formula)}
If you're graphing a polar equation, then write it in the form of: function {r -
formula}
POV-Ray's internal method of wrapping function values winds up hiding negative
vs positive parts,
and won't be revealed until made as an isosurface, or the function is shifted
by + 0.5 and visualized with a color map
If you're using functions that return values in the 0-255 range, you're going to
have to divide the result by 255
If the function repeats over a range of 0-255, then you're going to have to use
mod (Function (x, y, z), 256)/255
You're going to need function versions of HSV to RGB to perform color
calculations
For full-color patterns, you're going to separate functions for r, g, and b,
plus an average texture using all 3 functions
There are common functions and operations that the function parser doesn't
recognize, and you'll have to write your own versions of
identifiers previously declared in a scene (even for loop iterators!) cannot
then be used in a function
If you're experiencing a blank pattern (all black/white/gray) then you have
likely forgotten to explicitly include x, y, and z into your function
argument list. If your function takes some value N as an argument, but also
uses x, y, or z, then you must #declare F = function (x, y, z, N) {}
If your pattern only appears in the first quadrant (upper right, both x and y
are positive), then you will likely need to use abs(X) and abs(y) in your
equation net> wrote:
(Still experimenting and struggling with various aspects of getting patterns
from other platforms to play well with SDL.)
> Hammering out that many equations one after the other ... has allowed me to learn
some new things and gain valuable i
nsights ...
OK, just to list the ones that I've written down so far:
(Questions, comments, and constructive criticism welcome as always)
Important tips to generate quality patterns from equations
----------------------------------------------------------
Be very careful with the use of parentheses - especially when + or - is in an
equation. Group terms.
You may want to declare different parts of a complex equation as separate
functions, then combine them in the final function
Use fmod instead of mod to get a regular repetition of a pattern across the
origin
HOWEVER, sometimes using mod in certain functions gives a better (more
expected) result - so try both
Use Mike Williams' "shell" trick for isosurfaces to give an infinitely thin line
a visible thickness
Change the line thickness to give definition to patterns that may not show up
with smaller values.
Some equations don't cross the zero/integer/mod threshold often enough to show
finer details. Multiply the
WHOLE equation (use parentheses) by a factor to increase the number of
lines/levels.
Zoom in or out to see pattern attributes that may not be visible or clearly
rendered.
If you're graphing y as a function of x, then you must write it in the form of:
function {y - formula} since when y=formula, the value is 0
If you're graphing a 2-argument function of both x and y, then you must write it
in the form of: function {(x - x_formula) + (y - y_formula)}
If you're graphing a polar equation, then write it in the form of: function {r -
formula}
POV-Ray's internal method of wrapping function values winds up hiding negative
vs positive parts,
and won't be revealed until made as an isosurface, or the function is shifted
by + 0.5 and visualized with a color map
If you're using functions that return values in the 0-255 range, you're going to
have to divide the result by 255
If the function repeats over a range of 0-255, then you're going to have to use
mod (Function (x, y, z), 256)/255
You're going to need function versions of HSV to RGB to perform color
calculations
For full-color patterns, you're going to separate functions for r, g, and b,
plus an average texture using all 3 functions
There are common functions and operations that the function parser doesn't
recognize, and you'll have to write your own versions of
identifiers previously declared in a scene (even for loop iterators!) cannot
then be used in a function
If you're experiencing a blank pattern (all black/white/gray) then you have
likely forgotten to explicitly include x, y, and z into your function
argument list. If your function takes some value N as an argument, but also
uses x, y, or z, then you must #declare F = function (x, y, z, N) {}
If your pattern only appears in the first quadrant (upper right, both x and y
are positive), then you will likely need to use abs(X) and abs(y) in your
equation
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()