I threw together this little inversive geometry doodle last night to just make
something fun after a long while.

I might do some Steiner porisms and Appolonian gasket type stuff at some point.
Hoping some hyperbolic geometry on a Poisson disk.

I think a plane-filling Appolonian gasket pattern would be super cool, with an
inversion iteration level as a pattern argument.

Anyway, what's going on here is that things that are defined IN the gray circle,
get inverted to the outside of the circle.  Circles not passing through the
center of the inversion circle stay circles, and circles passing through the
center get inverted to lines (circles of infinite radius).  Tangency is
preserved.

Likewise, objects defined outside of the circle get inverted to the inside of
the gray circle.

The closer things are to the circle, the closer they are inverted, and the
closer they are to the center, the farther away they are, and the center maps to
"a point at infinity".

Rather than doing several pages of Euclidean geometry like Pappus, we use Felix
Klein's inversive geometry to leverage the special properties mentioned above.

We make 2 circles that pass through the center, and so get mapped to lines.
A circle tangent to both of those circles (blue) gets mapped to a circle outside
the inversion circle, and is tangent to the 2 lines from the inverted circles.
Then, since all of the subsequent circles are tangent to both of the circles and
the small circle next to it, they are easily made as circles outside the
inversion circle that are all just stacked circles of the same radius - they are
tangent to both lines and the circles next to them.
So when they get inverted to the inside of the circle, they preserve those
properties of tangency.

And out pops a Pappus chain.  Easy peasy.

- BE

Post a reply to this message

Attachments:
Download 'pappuschain.png' (75 KB)

Preview of image 'pappuschain.png'

On 5/28/24 19:41, Bald Eagle wrote:
> And out pops a Pappus chain.
Cool!

Bill P.

Post a reply to this message

William F Pokorny <ano### [at] anonymousorg> wrote:

> Cool!


Isn't it?

You can invert anything, even whole patterns, like so:

#declare Inversion = function {Radius*Radius / ( pow (x-CenterX, 2) + pow
(y-CenterY, 2) + pow (z-CenterZ, 2))}

#declare Checker_Inv = function {
 Checker (
  x*Inversion (x, y, z),
  y*Inversion (x, y, z),
  z*Inversion (x, y, z)
 ).red
}

plane {z, 0 pigment {function {Checker_Inv (x, y, z)}}}


I was trying to figure out a way to plug this into a matrix transform, but
POV-Ray doesn't allow that kind of thing.

/*
#declare M_Inversion =
function {
 transform {
  matrix <
   Inversion (x, y, z), 0, 0,
   0, Inversion (x, y, z), 0,
   0, 0, Inversion (x, y, z),
   0, 0, 0
  >
 }
}
*/

Post a reply to this message

On 5/29/24 06:54, Bald Eagle wrote:
> You can invert anything, even whole patterns, like so:

Thanks for posting more detailed code. I played a little - and it's cool 
- though the results kinda twist my head around at times. :-)

Attached is a slice of a sphere to the -z side of the x,y plane where 
the radius of a f_sphere() is getting 'inverted / chopped' with your 
'Checker_Inv()' (I also clamped the maximum Inversion() value to 15). 
The sides sliced at the inversions don't render cleanly with the 
isosurface, but we still end up with an interesting looking shape.

A little surprised it worked as well as it did...

Bill P.

FYI. I did get a few divisions by zero from Inversion() until I added 
some off grid, anti-directional, numerical fuzz to CenterX, CenterY and 
CenterZ. This might be due how my yuqk AA works compared to the 
officially released AA.

Post a reply to this message

Attachments:
Download 'tmp2.png' (105 KB)

Preview of image 'tmp2.png'

So that's very cool, and I wondered what it would look like if rendered as a
whole sphere, maybe with a glass texture and some sort of variation of the color
- perhaps determined by the Manhattan distance from the center.

I just used a quick, textured box, and the larger the inversion circle, the
smaller / more compact the pattern.   Patterns jump out at different scales.

Post a reply to this message

Attachments:
Download 'invertedpatternsphere.png' (262 KB)

Preview of image 'invertedpatternsphere.png'

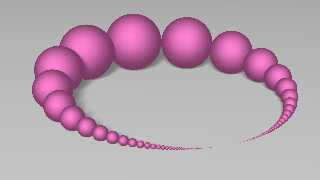
Ever inspired by the talented Francesco De Comite, I made a 3D version as a
little doodle.

Post a reply to this message

Attachments:
Download '3dpappuschain.png' (935 KB)

Preview of image '3dpappuschain.png'

On 12/06/2024 03:03, Bald Eagle wrote:
> Ever inspired by the talented Francesco De Comite, I made a 3D version as a
> little doodle.
> 

You have contaminated me ;)





-- 
Kurtz le pirate
Compagnie de la Banquise

Post a reply to this message

Attachments:
Download 'papus3.png' (201 KB)

Preview of image 'papus3.png'

kurtz le pirate <kur### [at] gmailcom> wrote:
> On 12/06/2024 03:03, Bald Eagle wrote:
> > Ever inspired by the talented Francesco De Comite, I made a 3D version as a
> > little doodle.
> >
>
> You have contaminated me ;)

You spelled "inspired" wrong.   :P

That's a beauty.
I'll bet that would amazing done in glass with caustics.
Or as stone spheres in a field of grass.

I still need to work out some good code for an Appolonian gasket.
(Unless you beat me to it  ;)  )

- BW

Post a reply to this message

"Bald Eagle" <cre### [at] netscapenet> wrote:

> I'll bet that would amazing done in glass with caustics.

Check out:

https://www.dumas.io/limset3d/

Post a reply to this message

On 12/06/2024 17:52, Bald Eagle wrote:
> I still need to work out some good code for an Appolonian gasket.
> (Unless you beat me to it  ;)  )



I'm working on it too.

wip here : <http://louisbel.free.fr/scenes/scene038.shtml>
(in french for the moment)





-- 
Kurtz le pirate
Compagnie de la Banquise

Post a reply to this message