 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> "jr" <cre### [at] gmail net> wrote:
> "jr" <cre### [at] gmail com> wrote:
>
> > v nice. I bet it would be "lush" as a woven fabric/cloth.
>
> There's a better one for that, I think - the "Honeycomb" that I found in a
> paper.
> Kinda looks like a "dog bone" wood patch that alternates in directions like a
> checkerboard.
Sometimes these things are a little easier to write using some helper functions.
#declare S2P = function (V) {sin (tau*V/L)}
#declare C2P = function (V) {cos (tau*V/L)}
#declare T = 0.5;
#declare N = 1;
#declare Honeycomb = function (X, Y, Z) {pow(S2P(X)*C2P(Z) + S2P(Z) + C2P(X), N)
- pow(T, N)} com> wrote:
>
> > v nice. I bet it would be "lush" as a woven fabric/cloth.
>
> There's a better one for that, I think - the "Honeycomb" that I found in a
> paper.
> Kinda looks like a "dog bone" wood patch that alternates in directions like a
> checkerboard.
Sometimes these things are a little easier to write using some helper functions.
#declare S2P = function (V) {sin (tau*V/L)}
#declare C2P = function (V) {cos (tau*V/L)}
#declare T = 0.5;
#declare N = 1;
#declare Honeycomb = function (X, Y, Z) {pow(S2P(X)*C2P(Z) + S2P(Z) + C2P(X), N)
- pow(T, N)}
Post a reply to this message
Attachments:
Download 'implicitlattice.png' (600 KB)
Preview of image 'implicitlattice.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
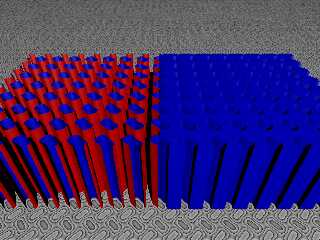
I think I was playing around with the AI again, and the simplest function caught
my eye.
Slumbering neurons were roused, and I realized that although I didn't have
access to POV-Ray, I _did_ have access to Desmos.
Graphing cos(x) * sin (y) revealed a very surprising pattern, and I did a little
bit of follow-up development from there. Subtracting a constant in between 0
and 1 changes the pattern from circles, to squircles, to squares.
So then, I had to transition between simple graphing, and mapping equations to a
plane with functions. I had a surprisingly difficult time getting the lines to
match the dots at the proper slopes, and I had to introduce fudge factors to get
the lines to accurately match the frequency of the dots.
Blah blah blah - here's the original basic pattern and the triangular grid that
I made based on that.
I also needed to alter my fmod function, and I still need to add another level
of select () to fix the doubling of the lines across N=0.
Post a reply to this message
Attachments:
Download 'mathpatterns2.png' (321 KB)
Preview of image 'mathpatterns2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> I also needed to alter my fmod function, and I still need to add another level
> of select () to fix the doubling of the lines across N=0.
I fixed that, and then added an averaged texture to throw some color into the
mix, and by using both functions and scaling the original pattern, you can see
how one relates to the other.
Bet you can even see the cubes and hexagons hidden in there... net> wrote:
> I also needed to alter my fmod function, and I still need to add another level
> of select () to fix the doubling of the lines across N=0.
I fixed that, and then added an averaged texture to throw some color into the
mix, and by using both functions and scaling the original pattern, you can see
how one relates to the other.
Bet you can even see the cubes and hexagons hidden in there...
Post a reply to this message
Attachments:
Download 'mathpatterns2.png' (555 KB)
Preview of image 'mathpatterns2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I cannot possibly imagine how they came up with this one.
Post a reply to this message
Attachments:
Download 'mathpatterns2.png' (149 KB)
Preview of image 'mathpatterns2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
>
Two older ones for your collection. Thing I found on the web years ago:
---%<------%<---
// Persistence of Vision Ray Tracer Scene Description File
// File: contour.pov
// Vers: 3.5
// Desc: contour plots Idea: Eric Weeks
// http://www.physics.emory.edu/~weeks/ideas/tplot.html
// Date: 2003
// Auth: Ingo Janssen
#version 3.5;
#include "gradients.inc"
//https://news.povray.org/povray.binaries.scene-files/message/%3CXnsA9D7C1F3776F3seed7%40news.povray.org%3E/#%3CXnsA9D7
C1F3776F3seed7%40news.povray.org%3E
global_settings {assumed_gamma 1.0}
camera {location <0,0,-25> look_at 0}
#declare Contour = function(x,y,z,A,B,C,D,E,F,I,J,K,L) {
E*sin(A*sin(I*x)+ B*cos(J*y))+F*cos(C*cos(K*x)+D*sin(L*y))
}
#declare A =1;
#declare B =1;
#declare C =1;
#declare D =1;
#declare E =1;
#declare F =1;
#declare I =1;
#declare J =1;
#declare K =1;
#declare L =1;
#declare Test = function(Pf){
(G_smoothstep(Pf,0.1,0.15)-G_smoothstep(Pf,0.15,0.2))
+(G_smoothstep(Pf,0.4,0.6)-G_smoothstep(Pf,0.7,.9))
};
plane {
-z, 0
pigment {
function{Contour(x,y,z,A,B,C,D,E,F,I,J,K,L)}
//function{G_Blinn_Wyvill(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//function{Test(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//function{abs(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//sine_wave
colour_map {
[0 rgb 0]
[1 rgb 1]
}
}
finish {ambient 1}
}
---%<------%<---
---%<------%<---
// POV-Ray 3.7
// Ingo
// found on a Japanese site
// +w1280 +h480 +a0.05 +am3 +ac0.90 +r3
#version 3.7;
global_settings{assumed_gamma 1}
#default{ finish{ambient 0 diffuse 1}}
camera {
orthographic
location <0,0,1>
look_at 0
right x*image_width/image_height
}
#declare PHI = 1.61803399;
// Shuhei Kawachi
// A>0
#declare ShuheiKawachi = function (x,y,z,A,B){
((cos(x)*cos(y)+cos((sqrt(A)*x-y)/B)*
cos((x+sqrt(A)*y)/B)+cos((sqrt(A)*x+y)/B)*
cos((x-sqrt(A)*y)/B)))/3///6 + 0.5
}
plane{ <0,0,-1>, 0
texture {
pigment {
//function{(ShuheiKawachi(x,y,z,pi,1.5))}
function{abs(ShuheiKawachi(x,y,z,pi,1.5))}
sine_wave
scale 0.02
}
finish {ambient 1 diffuse 0}
}
}
---%<------%<---
ingo net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
>
Two older ones for your collection. Thing I found on the web years ago:
---%<------%<---
// Persistence of Vision Ray Tracer Scene Description File
// File: contour.pov
// Vers: 3.5
// Desc: contour plots Idea: Eric Weeks
// http://www.physics.emory.edu/~weeks/ideas/tplot.html
// Date: 2003
// Auth: Ingo Janssen
#version 3.5;
#include "gradients.inc"
//https://news.povray.org/povray.binaries.scene-files/message/%3CXnsA9D7C1F3776F3seed7%40news.povray.org%3E/#%3CXnsA9D7
C1F3776F3seed7%40news.povray.org%3E
global_settings {assumed_gamma 1.0}
camera {location <0,0,-25> look_at 0}
#declare Contour = function(x,y,z,A,B,C,D,E,F,I,J,K,L) {
E*sin(A*sin(I*x)+ B*cos(J*y))+F*cos(C*cos(K*x)+D*sin(L*y))
}
#declare A =1;
#declare B =1;
#declare C =1;
#declare D =1;
#declare E =1;
#declare F =1;
#declare I =1;
#declare J =1;
#declare K =1;
#declare L =1;
#declare Test = function(Pf){
(G_smoothstep(Pf,0.1,0.15)-G_smoothstep(Pf,0.15,0.2))
+(G_smoothstep(Pf,0.4,0.6)-G_smoothstep(Pf,0.7,.9))
};
plane {
-z, 0
pigment {
function{Contour(x,y,z,A,B,C,D,E,F,I,J,K,L)}
//function{G_Blinn_Wyvill(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//function{Test(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//function{abs(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//sine_wave
colour_map {
[0 rgb 0]
[1 rgb 1]
}
}
finish {ambient 1}
}
---%<------%<---
---%<------%<---
// POV-Ray 3.7
// Ingo
// found on a Japanese site
// +w1280 +h480 +a0.05 +am3 +ac0.90 +r3
#version 3.7;
global_settings{assumed_gamma 1}
#default{ finish{ambient 0 diffuse 1}}
camera {
orthographic
location <0,0,1>
look_at 0
right x*image_width/image_height
}
#declare PHI = 1.61803399;
// Shuhei Kawachi
// A>0
#declare ShuheiKawachi = function (x,y,z,A,B){
((cos(x)*cos(y)+cos((sqrt(A)*x-y)/B)*
cos((x+sqrt(A)*y)/B)+cos((sqrt(A)*x+y)/B)*
cos((x-sqrt(A)*y)/B)))/3///6 + 0.5
}
plane{ <0,0,-1>, 0
texture {
pigment {
//function{(ShuheiKawachi(x,y,z,pi,1.5))}
function{abs(ShuheiKawachi(x,y,z,pi,1.5))}
sine_wave
scale 0.02
}
finish {ambient 1 diffuse 0}
}
}
---%<------%<---
ingo
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
An old one by Alex Kluchikov, not a simple function though:
---%<------%<---
// Alex Kluchikov, 2003
// mailto: klk### [at] ukr net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
An old one by Alex Kluchikov, not a simple function though:
---%<------%<---
// Alex Kluchikov, 2003
// mailto: klk### [at] ukr net, akl### [at] mail net, akl### [at] mail ru
// Feel free to modify/use in any form
include "functions.inc"
camera{
location -5*z
look_at 0
}
// we can get angle from gradient
#declare frad=function{
pattern{radial}
}
#declare fboz1=function{
pattern{crackle form <1,0,0> scale 1}
}
#declare fboz2=function{
pattern{bumps noise_generator 3 rotate 60 scale 1.2}
}
#declare fboz3=function{
(sin(x+23)*sin(y+2)+sin(x*2.33443+11)*sin(y*2.4332+76)+sin(x*1.133443+32)*sin(y*1.234332+8)+3)*1/6
}
#declare f1=function(x,y,z){
(sin(fboz1(x,y,z)*24*pi
+frad(fboz1(x,y,z)-fboz1(x,y-.07,z),0,fboz1(x,y,z)-fboz1(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
*(1-fboz1(x,y,z))
}
#declare f2=function(x,y,z){
(sin(fboz2(x,y,z)*24*pi
+frad(fboz2(x,y,z)-fboz2(x,y-.07,z),0,fboz2(x,y,z)-fboz2(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
}
#declare f3=function(x,y,z){
(sin(fboz3(x,y,z)*24*pi
+frad(fboz3(x,y,z)-fboz3(x,y-.07,z),0,fboz3(x,y,z)-fboz3(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
}
#declare curles_1=texture{pigment{
function{f1(x,y,z)}
scale .25}
finish{ambient 1}
}
#declare curles_2=texture{pigment{
function{f2(x,y,z)}
color_map{[.45,color rgb 0][.55,color rgb 1]}
scale .25}
finish{ambient 1}
}
#declare curles_3=texture{pigment{
function{f3(x,y,z)}
color_map{[.45,color rgb 0][.55,color rgb 1]}
scale .25}
finish{ambient 1}
}
plane{
-z,1
//use curles_1, curles_2 or curles_2
texture{curles_1}
}
---%<------%<------
ingo ru
// Feel free to modify/use in any form
include "functions.inc"
camera{
location -5*z
look_at 0
}
// we can get angle from gradient
#declare frad=function{
pattern{radial}
}
#declare fboz1=function{
pattern{crackle form <1,0,0> scale 1}
}
#declare fboz2=function{
pattern{bumps noise_generator 3 rotate 60 scale 1.2}
}
#declare fboz3=function{
(sin(x+23)*sin(y+2)+sin(x*2.33443+11)*sin(y*2.4332+76)+sin(x*1.133443+32)*sin(y*1.234332+8)+3)*1/6
}
#declare f1=function(x,y,z){
(sin(fboz1(x,y,z)*24*pi
+frad(fboz1(x,y,z)-fboz1(x,y-.07,z),0,fboz1(x,y,z)-fboz1(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
*(1-fboz1(x,y,z))
}
#declare f2=function(x,y,z){
(sin(fboz2(x,y,z)*24*pi
+frad(fboz2(x,y,z)-fboz2(x,y-.07,z),0,fboz2(x,y,z)-fboz2(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
}
#declare f3=function(x,y,z){
(sin(fboz3(x,y,z)*24*pi
+frad(fboz3(x,y,z)-fboz3(x,y-.07,z),0,fboz3(x,y,z)-fboz3(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
}
#declare curles_1=texture{pigment{
function{f1(x,y,z)}
scale .25}
finish{ambient 1}
}
#declare curles_2=texture{pigment{
function{f2(x,y,z)}
color_map{[.45,color rgb 0][.55,color rgb 1]}
scale .25}
finish{ambient 1}
}
#declare curles_3=texture{pigment{
function{f3(x,y,z)}
color_map{[.45,color rgb 0][.55,color rgb 1]}
scale .25}
finish{ambient 1}
}
plane{
-z,1
//use curles_1, curles_2 or curles_2
texture{curles_1}
}
---%<------%<------
ingo
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Ha!
I think I have one of his "curles" patterns printed out somewhere here in a
pile.
I was just sifting through the archives and pulling out anything that seemed to
pop out.
Hopefully you know a few more - as you can tell, I love this stuff.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I've also been interested in making this pattern:
http://sambrunacini.com/wp-content/uploads/2020/10/pursuit.png
and I could have sworn it has an actual NAME that I found once, and now I of
course can't find again.
Also of interest would be a metal diamond-plate pattern - the "honeycomb"
pattern that I posted for jr has that alternating direction / row attribute that
might be a good starting point for modification.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Also of interest would be a metal diamond-plate pattern - the "honeycomb"
> pattern that I posted for jr has that alternating direction / row attribute that
> might be a good starting point for modification.
#declare YY = 0.625;
#declare Plate1 = function {select (1-pow(sin(2*pi*x)*cos(2*pi*YY) +
sin(2*pi*YY)*cos(2*pi*z) + sin(2*pi*z)*cos(2*pi*x), 2), 0, 0, 1)} net> wrote:
> Also of interest would be a metal diamond-plate pattern - the "honeycomb"
> pattern that I posted for jr has that alternating direction / row attribute that
> might be a good starting point for modification.
#declare YY = 0.625;
#declare Plate1 = function {select (1-pow(sin(2*pi*x)*cos(2*pi*YY) +
sin(2*pi*YY)*cos(2*pi*z) + sin(2*pi*z)*cos(2*pi*x), 2), 0, 0, 1)}
Post a reply to this message
Attachments:
Download 'mathpatterns2.png' (237 KB)
Preview of image 'mathpatterns2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
"Bald Eagle" <cre### [at] netscape net> wrote:
> ...
> > Kinda looks like a "dog bone" wood patch that alternates in directions like a
> > checkerboard.
>
> Sometimes these things are a little easier to write using some helper functions.
>
> #declare S2P = function (V) {sin (tau*V/L)}
> #declare C2P = function (V) {cos (tau*V/L)}
> #declare T = 0.5;
> #declare N = 1;
> #declare Honeycomb = function (X, Y, Z) {pow(S2P(X)*C2P(Z) + S2P(Z) + C2P(X), N)
> - pow(T, N)}
plane with "Honeycomb" pattern, seen through "kaleidoscope".
regards, jr. net> wrote:
> ...
> > Kinda looks like a "dog bone" wood patch that alternates in directions like a
> > checkerboard.
>
> Sometimes these things are a little easier to write using some helper functions.
>
> #declare S2P = function (V) {sin (tau*V/L)}
> #declare C2P = function (V) {cos (tau*V/L)}
> #declare T = 0.5;
> #declare N = 1;
> #declare Honeycomb = function (X, Y, Z) {pow(S2P(X)*C2P(Z) + S2P(Z) + C2P(X), N)
> - pow(T, N)}
plane with "Honeycomb" pattern, seen through "kaleidoscope".
regards, jr.
Post a reply to this message
Attachments:
Download 'ktpms.png' (440 KB)
Preview of image 'ktpms.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()