 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
This is very similar in concept to the Voronoi pattern, and indeed, if the
"annular rings" are fine enough, one gets the visual impression of Voronoi cells
filled with a concentric ring pattern.
I just did this for fun, to illustrate a practical pattern to use for ripples in
water, malachite, rhodochrosite, wood, "jawbreaker" candies, etc, and to
implement an example that makes use of splines, loops, pseudorandom numbers, and
a discrete set of "basis functions" that are evaluated "en-masse".
Enjoy the "bubbles".
(Speaking of which, this could be a fun one to apply iridescence to...)
I'd have to think about how to vary the "radius" of each seed point, and then
apply the true bubble intersection formula to get a nice foam cross-section.
Foam isosurface, anyone?
- BE
Post a reply to this message
Attachments:
Download 'mathpatterns1.png' (704 KB)
Preview of image 'mathpatterns1.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Triply Periodic Minimal Surface
left - open
right - closed
plane - pigment {function {TPMS}}
This one is called "SplitP"
Post a reply to this message
Attachments:
Download 'implicitlattice.png' (711 KB)
Preview of image 'implicitlattice.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
"Bald Eagle" <cre### [at] netscape net> wrote:
> ...
> plane - pigment {function {TPMS}}
v nice. I bet it would be "lush" as a woven fabric/cloth.
(light-green with envy :-))
regards, jr. net> wrote:
> ...
> plane - pigment {function {TPMS}}
v nice. I bet it would be "lush" as a woven fabric/cloth.
(light-green with envy :-))
regards, jr.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"jr" <cre### [at] gmail com> wrote:
> v nice. I bet it would be "lush" as a woven fabric/cloth.
There's a better one for that, I think - the "Honeycomb" that I found in a
paper.
Kinda looks like a "dog bone" wood patch that alternates in directions like a
checkerboard.
A lot of these are, incidentally, used for support-fill for 3D printing
applications - so Kenneth may have a very practical interest.
Since they can partition space into 2 parts acting as a membrane in between,
when they are given thickness and made of metal, they are being evaluated as
heat-transfer devices, very much like a car radiator works.
The key factor being the very high surface area able to be contained in a very
small space.
> (light-green with envy :-))
You shouldn't be. You can copy-paste equations as well as I can. :P
- BW com> wrote:
> v nice. I bet it would be "lush" as a woven fabric/cloth.
There's a better one for that, I think - the "Honeycomb" that I found in a
paper.
Kinda looks like a "dog bone" wood patch that alternates in directions like a
checkerboard.
A lot of these are, incidentally, used for support-fill for 3D printing
applications - so Kenneth may have a very practical interest.
Since they can partition space into 2 parts acting as a membrane in between,
when they are given thickness and made of metal, they are being evaluated as
heat-transfer devices, very much like a car radiator works.
The key factor being the very high surface area able to be contained in a very
small space.
> (light-green with envy :-))
You shouldn't be. You can copy-paste equations as well as I can. :P
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
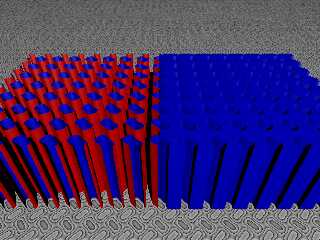
"Bald Eagle" <cre### [at] netscape net> wrote:
> "jr" <cre### [at] gmail net> wrote:
> "jr" <cre### [at] gmail com> wrote:
>
> > v nice. I bet it would be "lush" as a woven fabric/cloth.
>
> There's a better one for that, I think - the "Honeycomb" that I found in a
> paper.
> Kinda looks like a "dog bone" wood patch that alternates in directions like a
> checkerboard.
Sometimes these things are a little easier to write using some helper functions.
#declare S2P = function (V) {sin (tau*V/L)}
#declare C2P = function (V) {cos (tau*V/L)}
#declare T = 0.5;
#declare N = 1;
#declare Honeycomb = function (X, Y, Z) {pow(S2P(X)*C2P(Z) + S2P(Z) + C2P(X), N)
- pow(T, N)} com> wrote:
>
> > v nice. I bet it would be "lush" as a woven fabric/cloth.
>
> There's a better one for that, I think - the "Honeycomb" that I found in a
> paper.
> Kinda looks like a "dog bone" wood patch that alternates in directions like a
> checkerboard.
Sometimes these things are a little easier to write using some helper functions.
#declare S2P = function (V) {sin (tau*V/L)}
#declare C2P = function (V) {cos (tau*V/L)}
#declare T = 0.5;
#declare N = 1;
#declare Honeycomb = function (X, Y, Z) {pow(S2P(X)*C2P(Z) + S2P(Z) + C2P(X), N)
- pow(T, N)}
Post a reply to this message
Attachments:
Download 'implicitlattice.png' (600 KB)
Preview of image 'implicitlattice.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I think I was playing around with the AI again, and the simplest function caught
my eye.
Slumbering neurons were roused, and I realized that although I didn't have
access to POV-Ray, I _did_ have access to Desmos.
Graphing cos(x) * sin (y) revealed a very surprising pattern, and I did a little
bit of follow-up development from there. Subtracting a constant in between 0
and 1 changes the pattern from circles, to squircles, to squares.
So then, I had to transition between simple graphing, and mapping equations to a
plane with functions. I had a surprisingly difficult time getting the lines to
match the dots at the proper slopes, and I had to introduce fudge factors to get
the lines to accurately match the frequency of the dots.
Blah blah blah - here's the original basic pattern and the triangular grid that
I made based on that.
I also needed to alter my fmod function, and I still need to add another level
of select () to fix the doubling of the lines across N=0.
Post a reply to this message
Attachments:
Download 'mathpatterns2.png' (321 KB)
Preview of image 'mathpatterns2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> I also needed to alter my fmod function, and I still need to add another level
> of select () to fix the doubling of the lines across N=0.
I fixed that, and then added an averaged texture to throw some color into the
mix, and by using both functions and scaling the original pattern, you can see
how one relates to the other.
Bet you can even see the cubes and hexagons hidden in there... net> wrote:
> I also needed to alter my fmod function, and I still need to add another level
> of select () to fix the doubling of the lines across N=0.
I fixed that, and then added an averaged texture to throw some color into the
mix, and by using both functions and scaling the original pattern, you can see
how one relates to the other.
Bet you can even see the cubes and hexagons hidden in there...
Post a reply to this message
Attachments:
Download 'mathpatterns2.png' (555 KB)
Preview of image 'mathpatterns2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I cannot possibly imagine how they came up with this one.
Post a reply to this message
Attachments:
Download 'mathpatterns2.png' (149 KB)
Preview of image 'mathpatterns2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
>
Two older ones for your collection. Thing I found on the web years ago:
---%<------%<---
// Persistence of Vision Ray Tracer Scene Description File
// File: contour.pov
// Vers: 3.5
// Desc: contour plots Idea: Eric Weeks
// http://www.physics.emory.edu/~weeks/ideas/tplot.html
// Date: 2003
// Auth: Ingo Janssen
#version 3.5;
#include "gradients.inc"
//https://news.povray.org/povray.binaries.scene-files/message/%3CXnsA9D7C1F3776F3seed7%40news.povray.org%3E/#%3CXnsA9D7
C1F3776F3seed7%40news.povray.org%3E
global_settings {assumed_gamma 1.0}
camera {location <0,0,-25> look_at 0}
#declare Contour = function(x,y,z,A,B,C,D,E,F,I,J,K,L) {
E*sin(A*sin(I*x)+ B*cos(J*y))+F*cos(C*cos(K*x)+D*sin(L*y))
}
#declare A =1;
#declare B =1;
#declare C =1;
#declare D =1;
#declare E =1;
#declare F =1;
#declare I =1;
#declare J =1;
#declare K =1;
#declare L =1;
#declare Test = function(Pf){
(G_smoothstep(Pf,0.1,0.15)-G_smoothstep(Pf,0.15,0.2))
+(G_smoothstep(Pf,0.4,0.6)-G_smoothstep(Pf,0.7,.9))
};
plane {
-z, 0
pigment {
function{Contour(x,y,z,A,B,C,D,E,F,I,J,K,L)}
//function{G_Blinn_Wyvill(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//function{Test(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//function{abs(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//sine_wave
colour_map {
[0 rgb 0]
[1 rgb 1]
}
}
finish {ambient 1}
}
---%<------%<---
---%<------%<---
// POV-Ray 3.7
// Ingo
// found on a Japanese site
// +w1280 +h480 +a0.05 +am3 +ac0.90 +r3
#version 3.7;
global_settings{assumed_gamma 1}
#default{ finish{ambient 0 diffuse 1}}
camera {
orthographic
location <0,0,1>
look_at 0
right x*image_width/image_height
}
#declare PHI = 1.61803399;
// Shuhei Kawachi
// A>0
#declare ShuheiKawachi = function (x,y,z,A,B){
((cos(x)*cos(y)+cos((sqrt(A)*x-y)/B)*
cos((x+sqrt(A)*y)/B)+cos((sqrt(A)*x+y)/B)*
cos((x-sqrt(A)*y)/B)))/3///6 + 0.5
}
plane{ <0,0,-1>, 0
texture {
pigment {
//function{(ShuheiKawachi(x,y,z,pi,1.5))}
function{abs(ShuheiKawachi(x,y,z,pi,1.5))}
sine_wave
scale 0.02
}
finish {ambient 1 diffuse 0}
}
}
---%<------%<---
ingo net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
>
Two older ones for your collection. Thing I found on the web years ago:
---%<------%<---
// Persistence of Vision Ray Tracer Scene Description File
// File: contour.pov
// Vers: 3.5
// Desc: contour plots Idea: Eric Weeks
// http://www.physics.emory.edu/~weeks/ideas/tplot.html
// Date: 2003
// Auth: Ingo Janssen
#version 3.5;
#include "gradients.inc"
//https://news.povray.org/povray.binaries.scene-files/message/%3CXnsA9D7C1F3776F3seed7%40news.povray.org%3E/#%3CXnsA9D7
C1F3776F3seed7%40news.povray.org%3E
global_settings {assumed_gamma 1.0}
camera {location <0,0,-25> look_at 0}
#declare Contour = function(x,y,z,A,B,C,D,E,F,I,J,K,L) {
E*sin(A*sin(I*x)+ B*cos(J*y))+F*cos(C*cos(K*x)+D*sin(L*y))
}
#declare A =1;
#declare B =1;
#declare C =1;
#declare D =1;
#declare E =1;
#declare F =1;
#declare I =1;
#declare J =1;
#declare K =1;
#declare L =1;
#declare Test = function(Pf){
(G_smoothstep(Pf,0.1,0.15)-G_smoothstep(Pf,0.15,0.2))
+(G_smoothstep(Pf,0.4,0.6)-G_smoothstep(Pf,0.7,.9))
};
plane {
-z, 0
pigment {
function{Contour(x,y,z,A,B,C,D,E,F,I,J,K,L)}
//function{G_Blinn_Wyvill(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//function{Test(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//function{abs(Contour(x,y,z,A,B,C,D,E,F,I,J,K,L))}
//sine_wave
colour_map {
[0 rgb 0]
[1 rgb 1]
}
}
finish {ambient 1}
}
---%<------%<---
---%<------%<---
// POV-Ray 3.7
// Ingo
// found on a Japanese site
// +w1280 +h480 +a0.05 +am3 +ac0.90 +r3
#version 3.7;
global_settings{assumed_gamma 1}
#default{ finish{ambient 0 diffuse 1}}
camera {
orthographic
location <0,0,1>
look_at 0
right x*image_width/image_height
}
#declare PHI = 1.61803399;
// Shuhei Kawachi
// A>0
#declare ShuheiKawachi = function (x,y,z,A,B){
((cos(x)*cos(y)+cos((sqrt(A)*x-y)/B)*
cos((x+sqrt(A)*y)/B)+cos((sqrt(A)*x+y)/B)*
cos((x-sqrt(A)*y)/B)))/3///6 + 0.5
}
plane{ <0,0,-1>, 0
texture {
pigment {
//function{(ShuheiKawachi(x,y,z,pi,1.5))}
function{abs(ShuheiKawachi(x,y,z,pi,1.5))}
sine_wave
scale 0.02
}
finish {ambient 1 diffuse 0}
}
}
---%<------%<---
ingo
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
An old one by Alex Kluchikov, not a simple function though:
---%<------%<---
// Alex Kluchikov, 2003
// mailto: klk### [at] ukr net> wrote:
> Over the last 2 days, I've fallen down the mathematical pattern rabbit hole, and
> have been experimenting with all manner of what can be done with a simple
> pigment {function {}}
> statement.
An old one by Alex Kluchikov, not a simple function though:
---%<------%<---
// Alex Kluchikov, 2003
// mailto: klk### [at] ukr net, akl### [at] mail net, akl### [at] mail ru
// Feel free to modify/use in any form
include "functions.inc"
camera{
location -5*z
look_at 0
}
// we can get angle from gradient
#declare frad=function{
pattern{radial}
}
#declare fboz1=function{
pattern{crackle form <1,0,0> scale 1}
}
#declare fboz2=function{
pattern{bumps noise_generator 3 rotate 60 scale 1.2}
}
#declare fboz3=function{
(sin(x+23)*sin(y+2)+sin(x*2.33443+11)*sin(y*2.4332+76)+sin(x*1.133443+32)*sin(y*1.234332+8)+3)*1/6
}
#declare f1=function(x,y,z){
(sin(fboz1(x,y,z)*24*pi
+frad(fboz1(x,y,z)-fboz1(x,y-.07,z),0,fboz1(x,y,z)-fboz1(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
*(1-fboz1(x,y,z))
}
#declare f2=function(x,y,z){
(sin(fboz2(x,y,z)*24*pi
+frad(fboz2(x,y,z)-fboz2(x,y-.07,z),0,fboz2(x,y,z)-fboz2(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
}
#declare f3=function(x,y,z){
(sin(fboz3(x,y,z)*24*pi
+frad(fboz3(x,y,z)-fboz3(x,y-.07,z),0,fboz3(x,y,z)-fboz3(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
}
#declare curles_1=texture{pigment{
function{f1(x,y,z)}
scale .25}
finish{ambient 1}
}
#declare curles_2=texture{pigment{
function{f2(x,y,z)}
color_map{[.45,color rgb 0][.55,color rgb 1]}
scale .25}
finish{ambient 1}
}
#declare curles_3=texture{pigment{
function{f3(x,y,z)}
color_map{[.45,color rgb 0][.55,color rgb 1]}
scale .25}
finish{ambient 1}
}
plane{
-z,1
//use curles_1, curles_2 or curles_2
texture{curles_1}
}
---%<------%<------
ingo ru
// Feel free to modify/use in any form
include "functions.inc"
camera{
location -5*z
look_at 0
}
// we can get angle from gradient
#declare frad=function{
pattern{radial}
}
#declare fboz1=function{
pattern{crackle form <1,0,0> scale 1}
}
#declare fboz2=function{
pattern{bumps noise_generator 3 rotate 60 scale 1.2}
}
#declare fboz3=function{
(sin(x+23)*sin(y+2)+sin(x*2.33443+11)*sin(y*2.4332+76)+sin(x*1.133443+32)*sin(y*1.234332+8)+3)*1/6
}
#declare f1=function(x,y,z){
(sin(fboz1(x,y,z)*24*pi
+frad(fboz1(x,y,z)-fboz1(x,y-.07,z),0,fboz1(x,y,z)-fboz1(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
*(1-fboz1(x,y,z))
}
#declare f2=function(x,y,z){
(sin(fboz2(x,y,z)*24*pi
+frad(fboz2(x,y,z)-fboz2(x,y-.07,z),0,fboz2(x,y,z)-fboz2(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
}
#declare f3=function(x,y,z){
(sin(fboz3(x,y,z)*24*pi
+frad(fboz3(x,y,z)-fboz3(x,y-.07,z),0,fboz3(x,y,z)-fboz3(x+.07,y,z))
//gradient calculation
*2*pi
// +clock*pi*2 // uncomment to animate
)+1)*(1/2)
}
#declare curles_1=texture{pigment{
function{f1(x,y,z)}
scale .25}
finish{ambient 1}
}
#declare curles_2=texture{pigment{
function{f2(x,y,z)}
color_map{[.45,color rgb 0][.55,color rgb 1]}
scale .25}
finish{ambient 1}
}
#declare curles_3=texture{pigment{
function{f3(x,y,z)}
color_map{[.45,color rgb 0][.55,color rgb 1]}
scale .25}
finish{ambient 1}
}
plane{
-z,1
//use curles_1, curles_2 or curles_2
texture{curles_1}
}
---%<------%<------
ingo
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()