|
 |
If at first your code conversion doesn't succeed:
Throw it out and find some better code! :)
I found some MUCH shorter code by John Burkardt, which for some reason still
seemed a bit wonky in terms of array indices (my favorite thing to debug), but I
got to work fairly quickly.
It spits out duplicate triangles, so it took me a bit to write a post-process to
weed those out and just get a list of the minimum number of triangles. That
part is still misbehaving - but the Delaunay triangulation works, at least.
Now I've got the dual of the Voronoi. :)
Enjoy.
Post a reply to this message
Attachments:
Download 'delaunaytriangulatetest2.png' (58 KB)
Preview of image 'delaunaytriangulatetest2.png'
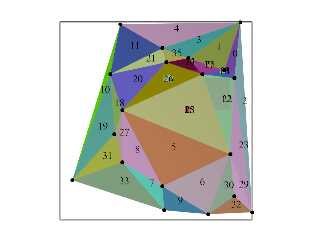
|
 |
|
 |
> It spits out duplicate triangles, so it took me a bit to write a post-process to
> weed those out and just get a list of the minimum number of triangles. That
> part is still misbehaving
I have 3 numbers in a "vector": x, y, and z.
That gives me 6 permutations.
I check them all.
It's not floating point, because they're all integer array indexes, and I even
wrote a custom VEq to test abs (N1-N2) < Threshold and that didn't improve
matters.
So I'm left again puzzling over why simple things like this are seemingly so
hard to code in SDL, and why the equivalency tests work in most cases, and fail
in others.
I mean, I start out with 162 triangles from the naive delaunay triangulation,
and trim it down to 35 - but some still slip through. :(
Pardon the code - it's got hacks and debugging cruft strewn all over the place
from trying to sort out all of the confusion.
Post a reply to this message
Attachments:
Download 'delaunaytriangulatetest2.pov.txt' (9 KB)
|
 |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> > It spits out duplicate triangles, so it took me a bit to write a post-process to
> > weed those out and just get a list of the minimum number of triangles. That
> > part is still misbehaving
>
> I have 3 numbers in a "vector": x, y, and z.
> That gives me 6 permutations.
> I check them all.
Aha.
I do check them all, but - What am I checking?
We do not realize how deeply our starting assumptions affect the way
we go about looking for and interpreting the data we collect.
I was checking the array indices of the Delaunay triangulation results.
My assumption? That they were unique - a 1:1 correspondence with the vertex
coordinates.
But NOOOOOOOOOOOOOO! They were not.
So the solution was to convert/expand the indices into proper vertex coordinate
vectors, and check THOSE against each other.
And Voila! No more duplicates. net> wrote:
> > It spits out duplicate triangles, so it took me a bit to write a post-process to
> > weed those out and just get a list of the minimum number of triangles. That
> > part is still misbehaving
>
> I have 3 numbers in a "vector": x, y, and z.
> That gives me 6 permutations.
> I check them all.
Aha.
I do check them all, but - What am I checking?
We do not realize how deeply our starting assumptions affect the way
we go about looking for and interpreting the data we collect.
I was checking the array indices of the Delaunay triangulation results.
My assumption? That they were unique - a 1:1 correspondence with the vertex
coordinates.
But NOOOOOOOOOOOOOO! They were not.
So the solution was to convert/expand the indices into proper vertex coordinate
vectors, and check THOSE against each other.
And Voila! No more duplicates.
Post a reply to this message
Attachments:
Download 'delaunaytriangulatetest2.png' (90 KB)
Preview of image 'delaunaytriangulatetest2.png'
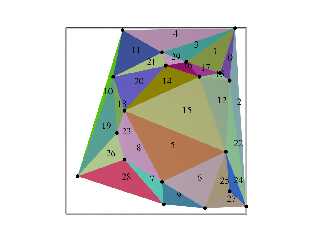
|
 |




![]()