 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
After a long hiatus, and extensive delays, a failing 1.5 TB drive, and 2
scrapped laptops, I reviewed enough calculus and read my collection of
differential geometry books and papers for the 50th time, so that I was able to
grasp enough of what I needed to do mathematically, to implement that in code.
It would make things easier if the nomenclature and symbols were consistent
throughout the literature, and some of the operations were better defined in the
papers themselves. Some of this was like sticking needles in my eyes.
Less than half of the struggle was the math, which turned out to not be that
difficult at all, and the more than half was descrambling all of the i's and j's
and getting the arrays laid out the right way so that the correct array elements
were getting plugged into the right places.
My analytical surface normals weren't right, but my central difference ones were
(?!) , and so I laid out all the tangents and normals and binormals of the
Frenet-Serret frames, which pointed to my curvature-related math being somehow
flipped across the diagonal with respect to my control points and Bezier
surface. Ugh.
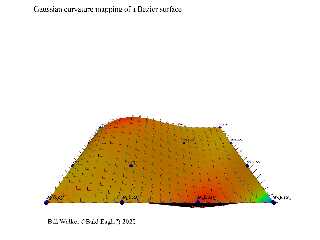
100 renders later, and I have a pretty hacky scene file that maps the Gaussian
curvature of a Bezier surface.
Never mind your p's and q's, pay detailed attention to your u's and v's!
I'm thinking that there MIGHT be a way to use some of the slope or AOI pigment
patterns to calculate the Frenet-Serret frames or any surface.... but that's
gonna require a lot more B12, coffee, and inner peace to puzzle out.
So, after a final week's struggle, here it is, a year later.
Post a reply to this message
Attachments:
Download '2022_surfacecurvatureattempt.png' (135 KB)
Preview of image '2022_surfacecurvatureattempt.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
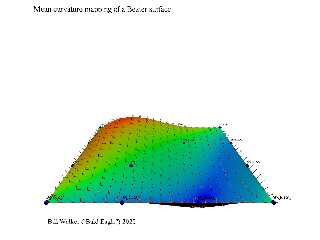
Using the same parameters that were calculated to obtain the First and Second
Fundamental Forms of the surface, the mean curvature can be mapped to the
surface as well.
Post a reply to this message
Attachments:
Download '2022_surfacecurvatureattempt.png' (151 KB)
Preview of image '2022_surfacecurvatureattempt.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Using the same parameters that were calculated to obtain the First and Second
> Fundamental Forms of the surface, the mean curvature can be mapped to the
> surface as well.
Could possible use of this if generalized be ? ...
dirt maps,
wear maps,
AO maps,
clay shaders,
https://www.shadertoy.com/view/fsGXzc
how does it differ from current AOI ? Is it able to reach further object space
angles? net> wrote:
> Using the same parameters that were calculated to obtain the First and Second
> Fundamental Forms of the surface, the mean curvature can be mapped to the
> surface as well.
Could possible use of this if generalized be ? ...
dirt maps,
wear maps,
AO maps,
clay shaders,
https://www.shadertoy.com/view/fsGXzc
how does it differ from current AOI ? Is it able to reach further object space
angles?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Mr" <m******r******at_hotmail_dot_fr> wrote:
> "Bald Eagle" <cre### [at] netscape net> wrote:
> > Using the same parameters that were calculated to obtain the First and Second
> > Fundamental Forms of the surface, the mean curvature can be mapped to the
> > surface as well.
>
> Could possible use of this if generalized be ? ...
>
> dirt maps,
> wear maps,
> AO maps,
> clay shaders,
Well, it's just an extension of the spline/surface matching that I was doing for
the monograph to make sure everything flows from one spline/surface to another
smoothly - and there are many levels of "smoothness".
Sometimes referred to as "fairing of a surface", techically referred to as C0,
C1, C2, ... and G0, G1, G2 ....
As for what its other possible us is, you know how we roll around here. People
might adapt it to anything they might think of.
> https://www.shadertoy.com/view/fsGXzc
>
> how does it differ from current AOI ?
AOI is just the angle between the surface normal and the camera
position-to-look-at vector. This is a function pattern that calculates the
curvature of the surface at every vertex (point) of a Bezier patch, given the 16
control points. It answers the (perhaps unasked) question, "How tightly is this
surface curled or dimpled?"
> Is it able to reach further object space angles?
Er..... I dunno.
Digging about in the archives of my HDD and the forums, I answered my question
about using uv maps and regular textures on the same object - clipka said that
was not currently possible. :(
I also re-answered my question about using the slope pattern in functions - it
can't be done, because it always returns zero, since it only truly gets
implemented and assigned values once it gets applied to the surface of an
object, under-the-hood.
I also found my re-write of TOK's VPerp_To_Vector macro, which had something to
do with Kenneth and greebles, but in typical fashion, I can't find the original
thread that started all of that.
So, it _might_ be able to be generalized, but it would be (yet another)
source-code level thing - so maybe Jerome Grimbert or Bill Pokorny could make it
happen in their respective forks.
Aside from that, I'm thinking that it could work sort of like the way you've
made carpets from image maps - we'd feed an object into a macro, and build a
surface in a piecewise fashion based on that. The only way I can currently see
doing that is using trace ().
I have a scene where I can plot the entire Frenet-Serret frame for all the
points on a Bezier surface just using trace (), but at the the moment, the
results are probably only valid because the points are on an axis-aligned grid.
The 2 vectors perpendicular to the normal give me the tangent and binormal,
which I'm treating as du and dv, and I'm assuming that a normalized vector
addition of those will give me duv. I still need the second partial derivatives
to get the curvature - and I have no real idea how to get that numerically or
geometrically except to do a sort of central differences type thing to assess
the concavity/convexity at each point.
No idea if any of that will work, but in typical fashion, I'll just plow ahead
like a blind bull in a china shop, and see what else I can break. :D
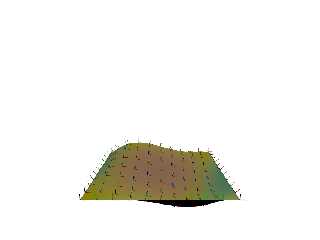
Attached is my WIP, with the surface texture an average of the x y and z slope
{} patterns, which I was naively hoping to use to encode the surface normal in a
function.
The stock VPerp_To_Vector gave me tangents and binormals pointing every which
way, but the rewrite made them all line up consistently. net> wrote:
> > Using the same parameters that were calculated to obtain the First and Second
> > Fundamental Forms of the surface, the mean curvature can be mapped to the
> > surface as well.
>
> Could possible use of this if generalized be ? ...
>
> dirt maps,
> wear maps,
> AO maps,
> clay shaders,
Well, it's just an extension of the spline/surface matching that I was doing for
the monograph to make sure everything flows from one spline/surface to another
smoothly - and there are many levels of "smoothness".
Sometimes referred to as "fairing of a surface", techically referred to as C0,
C1, C2, ... and G0, G1, G2 ....
As for what its other possible us is, you know how we roll around here. People
might adapt it to anything they might think of.
> https://www.shadertoy.com/view/fsGXzc
>
> how does it differ from current AOI ?
AOI is just the angle between the surface normal and the camera
position-to-look-at vector. This is a function pattern that calculates the
curvature of the surface at every vertex (point) of a Bezier patch, given the 16
control points. It answers the (perhaps unasked) question, "How tightly is this
surface curled or dimpled?"
> Is it able to reach further object space angles?
Er..... I dunno.
Digging about in the archives of my HDD and the forums, I answered my question
about using uv maps and regular textures on the same object - clipka said that
was not currently possible. :(
I also re-answered my question about using the slope pattern in functions - it
can't be done, because it always returns zero, since it only truly gets
implemented and assigned values once it gets applied to the surface of an
object, under-the-hood.
I also found my re-write of TOK's VPerp_To_Vector macro, which had something to
do with Kenneth and greebles, but in typical fashion, I can't find the original
thread that started all of that.
So, it _might_ be able to be generalized, but it would be (yet another)
source-code level thing - so maybe Jerome Grimbert or Bill Pokorny could make it
happen in their respective forks.
Aside from that, I'm thinking that it could work sort of like the way you've
made carpets from image maps - we'd feed an object into a macro, and build a
surface in a piecewise fashion based on that. The only way I can currently see
doing that is using trace ().
I have a scene where I can plot the entire Frenet-Serret frame for all the
points on a Bezier surface just using trace (), but at the the moment, the
results are probably only valid because the points are on an axis-aligned grid.
The 2 vectors perpendicular to the normal give me the tangent and binormal,
which I'm treating as du and dv, and I'm assuming that a normalized vector
addition of those will give me duv. I still need the second partial derivatives
to get the curvature - and I have no real idea how to get that numerically or
geometrically except to do a sort of central differences type thing to assess
the concavity/convexity at each point.
No idea if any of that will work, but in typical fashion, I'll just plow ahead
like a blind bull in a china shop, and see what else I can break. :D
Attached is my WIP, with the surface texture an average of the x y and z slope
{} patterns, which I was naively hoping to use to encode the surface normal in a
function.
The stock VPerp_To_Vector gave me tangents and binormals pointing every which
way, but the rewrite made them all line up consistently.
Post a reply to this message
Attachments:
Download 'surfacepropertiespattern.png' (68 KB)
Preview of image 'surfacepropertiespattern.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Aside from that, I'm thinking that it could work sort of like the way you've
> made carpets from image maps - we'd feed an object into a macro, and build a
> surface in a piecewise fashion based on that. The only way I can currently see
> doing that is using trace ().
>
> I have a scene where I can plot the entire Frenet-Serret frame for all the
> points on a Bezier surface just using trace (), but at the the moment, the
> results are probably only valid because the points are on an axis-aligned grid.
>
> The 2 vectors perpendicular to the normal give me the tangent and binormal,
> which I'm treating as du and dv, and I'm assuming that a normalized vector
> addition of those will give me duv. I still need the second partial derivatives
> to get the curvature - and I have no real idea how to get that numerically or
> geometrically except to do a sort of central differences type thing to assess
> the concavity/convexity at each point.
>
> No idea if any of that will work, but in typical fashion, I'll just plow ahead
> like a blind bull in a china shop, and see what else I can break. :D
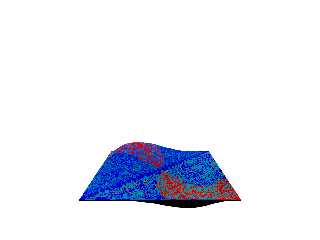
So, I rode the struggle bus and after a whole lot of plotting black spheres,
finally jiggled things so that I get some sort of color differentiation. I
suppose it very loosely resembles the Gaussian curvature render, so it's a step
in the right direction.
It's gonna need to store all of the results in an array so I can get the min &
max and normalize the result for the color map. But the biggest limitation is
of course the usual problems involving trace () - you just can't get into
overhangs and other occluded areas that the trace () ray hits first.
Probably gonna be one of those things where it's only good for Bezier patches
and parametric objects. Possibly isosurfaces. net> wrote:
> Aside from that, I'm thinking that it could work sort of like the way you've
> made carpets from image maps - we'd feed an object into a macro, and build a
> surface in a piecewise fashion based on that. The only way I can currently see
> doing that is using trace ().
>
> I have a scene where I can plot the entire Frenet-Serret frame for all the
> points on a Bezier surface just using trace (), but at the the moment, the
> results are probably only valid because the points are on an axis-aligned grid.
>
> The 2 vectors perpendicular to the normal give me the tangent and binormal,
> which I'm treating as du and dv, and I'm assuming that a normalized vector
> addition of those will give me duv. I still need the second partial derivatives
> to get the curvature - and I have no real idea how to get that numerically or
> geometrically except to do a sort of central differences type thing to assess
> the concavity/convexity at each point.
>
> No idea if any of that will work, but in typical fashion, I'll just plow ahead
> like a blind bull in a china shop, and see what else I can break. :D
So, I rode the struggle bus and after a whole lot of plotting black spheres,
finally jiggled things so that I get some sort of color differentiation. I
suppose it very loosely resembles the Gaussian curvature render, so it's a step
in the right direction.
It's gonna need to store all of the results in an array so I can get the min &
max and normalize the result for the color map. But the biggest limitation is
of course the usual problems involving trace () - you just can't get into
overhangs and other occluded areas that the trace () ray hits first.
Probably gonna be one of those things where it's only good for Bezier patches
and parametric objects. Possibly isosurfaces.
Post a reply to this message
Attachments:
Download 'surfacepropertiespattern.png' (158 KB)
Preview of image 'surfacepropertiespattern.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
"Bald Eagle" <cre### [at] netscape net> wrote:
> ...
> So, I rode the struggle bus and after a whole lot of plotting black spheres,
> finally jiggled things so that I get some sort of color differentiation. ...
no idea what it might be "good for" but looks intriguing. (the 2nd image made
me wonder, could the data be used to simulate something like a marble run :-))
regards, jr. net> wrote:
> ...
> So, I rode the struggle bus and after a whole lot of plotting black spheres,
> finally jiggled things so that I get some sort of color differentiation. ...
no idea what it might be "good for" but looks intriguing. (the 2nd image made
me wonder, could the data be used to simulate something like a marble run :-))
regards, jr.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> ...
> I also found my re-write of TOK's VPerp_To_Vector macro, which had something to
> do with Kenneth and greebles, but in typical fashion, I can't find the original
> thread that started all of that.
> ...
I guess that you are looking for this thread:
From: Robert McGregor
Subject: Sci-Fi Scene Assets
Date and time: 2021-02-17 22:25:01
https://news.povray.org/povray.binaries.images/thread/%3Cweb.603a1a16a906d8e3d98418910%40news.povray.org%3E/
It can be found with this Google search:
https://www.google.com/search?q=VPerp_To_Vector+Kenneth+greebles
;-)
Here's a part in this that thread that seems relevant:
https://news.povray.org/povray.binaries.images/thread/%3Cweb.602dddf4e63e50ad87570eab0%40news.povray.org%3E/?mtop=43394
8&moff=37
I posted this message in that thread:
From: Tor Olav Kristensen
Subject: Re: Sci-Fi Scene Assets
Date and time: 2021-04-16 23:55:00
- and some more in this part of the thread:
https://news.povray.org/povray.binaries.images/thread/%3Cweb.602dddf4e63e50ad87570eab0%40news.povray.org%3E/?mtop=43394
8&moff=87
- in reply to your post:
From: Bald Eagle
Subject: Re: Sci-Fi Scene Assets
Date and time: 2021-03-01 15:35:06
Btw: Your gaussian curvature work seem interesting.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
> ...
> I also found my re-write of TOK's VPerp_To_Vector macro, which had something to
> do with Kenneth and greebles, but in typical fashion, I can't find the original
> thread that started all of that.
> ...
I guess that you are looking for this thread:
From: Robert McGregor
Subject: Sci-Fi Scene Assets
Date and time: 2021-02-17 22:25:01
https://news.povray.org/povray.binaries.images/thread/%3Cweb.603a1a16a906d8e3d98418910%40news.povray.org%3E/
It can be found with this Google search:
https://www.google.com/search?q=VPerp_To_Vector+Kenneth+greebles
;-)
Here's a part in this that thread that seems relevant:
https://news.povray.org/povray.binaries.images/thread/%3Cweb.602dddf4e63e50ad87570eab0%40news.povray.org%3E/?mtop=43394
8&moff=37
I posted this message in that thread:
From: Tor Olav Kristensen
Subject: Re: Sci-Fi Scene Assets
Date and time: 2021-04-16 23:55:00
- and some more in this part of the thread:
https://news.povray.org/povray.binaries.images/thread/%3Cweb.602dddf4e63e50ad87570eab0%40news.povray.org%3E/?mtop=43394
8&moff=87
- in reply to your post:
From: Bald Eagle
Subject: Re: Sci-Fi Scene Assets
Date and time: 2021-03-01 15:35:06
Btw: Your gaussian curvature work seem interesting.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> It can be found with this Google search:
>
> https://www.google.com/search?q=VPerp_To_Vector+Kenneth+greebles
That is totally what I did, in like 7 different ways. I didn't get that thread
as a search result though.
> Btw: Your gaussian curvature work seem interesting.
Thanks - just needed to clear my head and have enough free time and mental
energy to trudge through all of the steps to get everything to play together
nicely.
I'll have to look into what other surface attributes can be color-mapped.
Wondering if there's a simple/quick way to "reverse uv-map" a curvature-textured
Bezier patch to yield a rectangular image map for further use. com> wrote:
> It can be found with this Google search:
>
> https://www.google.com/search?q=VPerp_To_Vector+Kenneth+greebles
That is totally what I did, in like 7 different ways. I didn't get that thread
as a search result though.
> Btw: Your gaussian curvature work seem interesting.
Thanks - just needed to clear my head and have enough free time and mental
energy to trudge through all of the steps to get everything to play together
nicely.
I'll have to look into what other surface attributes can be color-mapped.
Wondering if there's a simple/quick way to "reverse uv-map" a curvature-textured
Bezier patch to yield a rectangular image map for further use.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> I'll have to look into what other surface attributes can be color-mapped.
>
> Wondering if there's a simple/quick way to "reverse uv-map" a curvature-textured
> Bezier patch to yield a rectangular image map for further use.
If you are able to store the color for each vertex in an array, then you can
just insert the same colors into a mesh2 within a plane in front of the camera,
with the coordinates within that plane equal to the UV-coordinates for the
colors.
POV-Ray can then interpolate the colors (texture) within each mesh2 triangle in
that plane from the color (texture) for each vertex.
See the last section at this page; about "a texture per vertex":
http://www.povray.org/documentation/view/3.7.1/68/
I did something similar in the TexturedTriangle() macro in this file:
https://github.com/t-o-k/POV-Ray-icosahedron/blob/main/Icosahedron_Coloured.pov
- in this repository:
https://github.com/t-o-k/POV-Ray-icosahedron
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
>...
> I'll have to look into what other surface attributes can be color-mapped.
>
> Wondering if there's a simple/quick way to "reverse uv-map" a curvature-textured
> Bezier patch to yield a rectangular image map for further use.
If you are able to store the color for each vertex in an array, then you can
just insert the same colors into a mesh2 within a plane in front of the camera,
with the coordinates within that plane equal to the UV-coordinates for the
colors.
POV-Ray can then interpolate the colors (texture) within each mesh2 triangle in
that plane from the color (texture) for each vertex.
See the last section at this page; about "a texture per vertex":
http://www.povray.org/documentation/view/3.7.1/68/
I did something similar in the TexturedTriangle() macro in this file:
https://github.com/t-o-k/POV-Ray-icosahedron/blob/main/Icosahedron_Coloured.pov
- in this repository:
https://github.com/t-o-k/POV-Ray-icosahedron
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"jr" <cre### [at] gmail com> wrote:
> no idea what it might be "good for" but looks intriguing. (the 2nd image made
> me wonder, could the data be used to simulate something like a marble run :-))
So, this is a video with information pertaining to Blender, but aside from the
general workflow and texture mapping/layering tricks, what caught my interest
was the "curvature map".
https://www.youtube.com/watch?v=-x-b2U-MSgc
I think that addresses the question "what can it be used for?" with regard to
the mean and Gaussian curvature of Bezier surfaces.
I'd still have to work out the numerical method for calculating the curvature of
ANY given surface, and that might be a bit slower, but the final results sure do
look promising.
- BE com> wrote:
> no idea what it might be "good for" but looks intriguing. (the 2nd image made
> me wonder, could the data be used to simulate something like a marble run :-))
So, this is a video with information pertaining to Blender, but aside from the
general workflow and texture mapping/layering tricks, what caught my interest
was the "curvature map".
https://www.youtube.com/watch?v=-x-b2U-MSgc
I think that addresses the question "what can it be used for?" with regard to
the mean and Gaussian curvature of Bezier surfaces.
I'd still have to work out the numerical method for calculating the curvature of
ANY given surface, and that might be a bit slower, but the final results sure do
look promising.
- BE
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()