"Kenneth" <kdw### [at] gmailcom> wrote:
> "Bald Eagle" <cre### [at] netscapenet> wrote:
> >
> > And then, as I discovered, after hunting down a curious line of code in Ingo's
> > vrand on sphere macro, that there's the matter of not just randomly
> > placed - but EVENLY placed.   The distributions can be quite tricky.
> >
> > Lets say we take a landscape heightfield and try to place objects onto
> > it.   If we just trace() straight down from an imaginary rectangle of
> > ray starting coordinates, then the regions of rapidly changing elevation
> > don't get as much arc-length coverage as the flat parts.
> >
>
> Yeah, that little problem has always been a thorny one to try and solve. But I
> just had a wild idea (possibly a naive one):
> It seems to me that the pixel positions of a *u-v map* of a HF might somehow be
> used to generate the trace-from points. Since the u-v map is by nature a
> 'stretched-out' representation of the HF itself-- covering all of the HF's area,
> and with more points or pixel positions than a typical
> 'trace-down-from-rectangular-area' scheme -- the uv-map's points or pixels could
> then be correlated (somehow) with the corresponding points on the HF... the
> result being to 'evenly' cover the HF with trace rays, even on steep elevations.
> That's what I see in my minds eye, anyway.

The rectangle's x,z coordinates are the exact same thing as the u,v coordinates
of the heightfield, in terms of the fact that you can't subdivide the u,v's any
differently than the x,z's.   Aside from scale and absolute location, they're
exactly the same.
What needs to be done is to calculate the arc length of the curve in the u or v
direction, and then compensate for that additional distance by clustering more
random samples in those areas.

https://www.mathwords.com/a/arc_length_of_a_curve.htm

This seems to be closely related to the "importance sampling" clipka was looking
for.... 5 years ago. :O
http://news.povray.org/povray.advanced-users/thread/%3C57bf8a2f%241%40news.povray.org%3E/?ttop=433049&toff=150&mtop=410
480

It's NOT trivial, but if it were simply a matter of investing the time to
one-time algorithmically process the hf for a scene and save the data to a file,
then it probably would be worth doing...

http://news.povray.org/web.60330f52d0c3b58b1f9dae300%40news.povray.org

Post a reply to this message

"Bald Eagle" <cre### [at] netscapenet> wrote:

> What needs to be done is to calculate the arc length of the curve in the u or v
> direction, and then compensate for that additional distance by clustering more
> random samples in those areas.

So, this just popped into my head, inspired by your comment and my thinking
about Vrand_on_Bezier -

There are the clock / spline macros that plot points uniformly over a spline.
Scan in the data across the u direction, saving to a spline / array, and
increment down the hf in the v direction.

Then rather than plot the point on the hf directly, plot it on the spline.

If those macros work for bezier splines, then that may be a solution for Cousin
Ricky's scene as well.

Post a reply to this message

Le 04/03/2021 à 20:22, Bald Eagle a écrit :

> What needs to be done is to calculate the arc length of the curve in the u or v
> direction, and then compensate for that additional distance by clustering more
> random samples in those areas.
> 
> https://www.mathwords.com/a/arc_length_of_a_curve.htm
> 

When someone says that every length can be computed, I am reminded of
the ellipse.

You can compute the area of the ellipse accurately, but not its perimeter.

And if you have a formula for the length of the perimeter of the
ellipse, a true formula, not an approximation, you are an alien.

Post a reply to this message

"Bald Eagle" <cre### [at] netscapenet> wrote:
> "Kenneth" <kdw### [at] gmailcom> wrote:

> > It seems to me that the pixel positions of a *u-v map* of a HF might
> > somehow be used to generate the trace-from points. Since the u-v map is
> > by nature a 'stretched-out' representation of the HF itself...
>
> The rectangle's x,z coordinates are the exact same thing as the u,v
> coordinates of the heightfield, in terms of the fact that you can't
> subdivide the u,v's any differently than the x,z's.

Yep, I get that.

I probably used the wrong nomenclature to describe what I mean. I meant to say,
"the pixel positions of the uv TEXTURE map (the generated image_map artwork
that's made in an app like UV Mapper.) In effect, a flat representation of the
'un-wrapped' HF. To initially get the trace-from positions-- not by initially
tracing the height_field itself (although that would also need to be done as a
2nd step, I think.)

Let's say that there are two triangles on the mesh HF that butt up against each
other. Assume that triangle #1 is almost flat horizontally, so it's a nice
little equilateral triangle. But triangle #2 turns out to have a very steep
slope on the HF, with its two base-points at almost 0.0 height, but its tip way
up at almost 1.0. So that triangle is extremely 'stretched', with more surface
area.

On the (flat) uv TEXTURE map or image_map, the 2nd triangle takes up lots more
space than triangle #1. Now assume that the final texture map has lots of these
different-sized triangluar areas.

That final image_map will have a 1X1 length-to-width ratio-- same as the
height_field square-- but obviously with some places that have NO representative
triangles on it; it's a visual representation of the un-folded HF, whatever odd
shape that turns out to be, 'pasted' onto a 1X1-ratio image size. But the lack
of triangles in some places is not really a problem for the scheme itself.

So my crazy idea is to randomly trace that TEXTURE map-- only for the 2-D
positions on it-- then to somehow correlate those found positions to the
'matching' triangles on the 3-D height_field, to finally place the greebles
during the subsequent (2nd) *HF*-tracing operation (using the typical top-down
tracing directions there, nothing fancy.) In my mind's eye, triangle
#1 will have a few 'hits', but triangle #2 will have *more* hits (because of its
larger surface area on the TEXTURE map)... in effect, making an 'even'
distribution of greeble placements on the HF itself.

Voila! Well, discounting the mathematical magic that would probably be required.
;-)

This is all conjecture, of course.

Post a reply to this message

"Kenneth" <kdw### [at] gmailcom> wrote:

> Voila! Well, discounting the mathematical magic that would probably be required.
> ;-)

I do see the main problem though, and it's a big one: How to correlate an
oddly-shaped total 'area' of triangles on the TEXTURE map (certainly not a 1X1
ratio area, and with an oddly-shaped perimeter) to the HF itself, which *is* a
1X1 ratio. It would be a strange scaling problem indeed.

:-(

Post a reply to this message

"Kenneth" <kdw### [at] gmailcom> wrote:
> "Kenneth" <kdw### [at] gmailcom> wrote:
>
> > Voila! Well, discounting the mathematical magic that would probably be required.
> > ;-)
>
> I do see the main problem though, and it's a big one: How to correlate an
> oddly-shaped total 'area' of triangles on the TEXTURE map (certainly not a 1X1
> ratio area, and with an oddly-shaped perimeter) to the HF itself, which *is* a
> 1X1 ratio. It would be a strange scaling problem indeed.
>
> :-(

Well serendipity and synchronicity strike again:
I was looking for some info to better explain the meaning of the core inequality
in the polygon test, and I found a video by Sebastian Lague

https://www.youtube.com/watch?v=HYAgJN3x4GA

with this link in the comment section:

https://chrischoy.github.io/research/barycentric-coordinate-for-mesh-sampling/

Post a reply to this message

"Bald Eagle" <cre### [at] netscapenet> wrote:

I've done the  VRand_ON_Box (RandSeed) awhile ago for my MeshTree project
along with VRand_ON_Cone,VRand_IN_Cone, VRand_ON_Cylinder, VRand_IN_Cylinder

I used them to place the end points of a binary tree.

When I looked back on them  I found that the Cone marcos use a cone with a base
pov unit from <0,0,0,> the end point 1 unit in opposite direction 1 with the
base radius 1 and the other radius 0 and you had a choice of 3 directions to
place it
(x,y,z). The On_Cone also had the OPEN option.
 The cylinder macro has the same basic lay out.

They work great for making trees but I don't know if they have an even
distribution.
Here they are copied from the modified rand.inc I use.

//a random point ON a square box {-1, 1}
#macro VRand_On_Box(R)// LR added
 #local V=<0,0,0>;
 #local a=int(rand(R)*6);
 #switch (a)
  #case(0)#local V=<-1,rand(R)*2-1,rand(R)*2-1>; #break
  #case(1)#local V=<1,rand(R)*2-1,rand(R)*2-1>; #break
  #case(2)#local V=<rand(R)*2-1,-1,rand(R)*2-1>; #break
  #case(3)#local V=<rand(R)*2-1,1,rand(R)*2-1>; #break
  #case(4)#local V=<rand(R)*2-1,rand(R)*2-1,-1>; #break
  #case(5)#local V=<rand(R)*2-1,rand(R)*2-1,1>; #break
  #end
  (V)
#end

//a random point ON a Cylinder from -1 to 1 in the D direction
// radius=1
// if O open cylinder
// D=1 +y direction
// D=2 +x direction
// D=3 +z direction
#macro VRand_On_Cyl(D,O,R)// LR added
   #local Theta = 2*pi*rand(R);
   #local V=<0,0,0>;
   #local H=rand(R)*2-1;
   #local S=1; // radius
   #if(O) #local Hv=1;
   #else  #local Hv=.95;
   #end
   #if (H>Hv) #local S=rand(R);#local H=1; #end
   #if (H<-Hv) #local S=rand(R);#local H=0; #end
   #if (D=1)#local V= <H,cos(Theta)*S,sin(Theta)*S>; #end
   #if (D=2)#local V= <cos(Theta)*S,H,sin(Theta)*S>; #end
   #if (D=3)#local V= <cos(Theta)*S,sin(Theta)*S,H>; #end
  (V)
#end

//a random point IN a Cylinder from -1 to 1 in the D direction
// D=1 +y direction
// D=2 +x direction
// D=3 +z direction
#macro VRand_In_Cyl(D,R)// LR added
   #local Theta = 2*pi*rand(R);
   #local V=<0,0,0>;
   #local H=rand(R)*2-1;
   #local S=rand(R);
   #if (D=1)#local V= <H,cos(Theta)*S,sin(Theta)*S>; #end
   #if (D=2)#local V= <cos(Theta)*S,H,sin(Theta)*S>; #end
   #if (D=3)#local V= <cos(Theta)*S,sin(Theta)*S,H>; #end
  (V)
#end
//a random point ON a Cone from -1,1 to 1,0 in the D direction
// more values in the lower part
// if O open Cone
// D=1 +x direction
// D=2 +y direction
// D=3 +z direction
#macro VRand_On_Cone(D,O,RS)// LR added
   #local Rt=rand(RS);
   #local Rv=Rt*Rt;
   #local Theta = 2*pi*rand(RS);
   #local V=<0,0,0>;
   #local H=Rv*2-1;
   #local S=1-(H+1)/2;
   #if(H<-.95 & O=0)  #local S=rand(RS); #local H=-1;#end
   #if (D=1)#local V= <H,cos(Theta)*S,sin(Theta)*S>; #end
   #if (D=2)#local V= <cos(Theta)*S,H,sin(Theta)*S>; #end
   #if (D=3)#local V= <cos(Theta)*S,sin(Theta)*S,H>; #end
  (V)
#end
//a random point IN a Cone from -1,1 to 1,0 in the D direction
// more values in the lower part
// D=1 +y direction
// D=2 +x direction
// D=3 +z direction
#macro VRand_In_Cone(D,RS)// LR added
   #local Rt=rand(RS);
   #local Rv=Rt*Rt;
   #local Theta = 2*pi*rand(RS);
   #local V=<0,0,0>;
   #local H=Rv*2-1;
   #local S=1-(H+1)/2;
   #local S=S*rand(RS);
   #if (D=1)#local V= <H,cos(Theta)*S,sin(Theta)*S>; #end
   #if (D=2)#local V= <cos(Theta)*S,H,sin(Theta)*S>; #end
   #if (D=3)#local V= <cos(Theta)*S,sin(Theta)*S,H>; #end
  (V)
#end

Post a reply to this message

Thanks, Leroy!   :)

It will be good to compare approaches.

The tricky part for getting an even distribution usually lies when there is a
variable radius term, as the density of the points changes.
I'll run your macros, get a visual idea, and see how things go.

Post a reply to this message

It's kind of scary when so many seemingly disparate topics that I've dipped my
toes into all get brought together into one pretty cool video.

Enjoy:

"The BEST Way to Find a Random Point in a Circle"
https://www.youtube.com/watch?v=4y_nmpv-9lI

Post a reply to this message

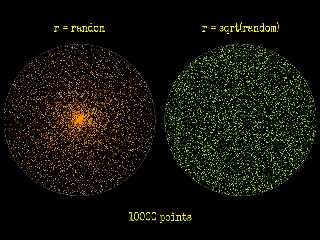
On 03/09/2023 02:44, Bald Eagle wrote:
> It's kind of scary when so many seemingly disparate topics that I've dipped my
> toes into all get brought together into one pretty cool video.
> 
> Enjoy:
> 
> "The BEST Way to Find a Random Point in a Circle"
> https://www.youtube.com/watch?v=4y_nmpv-9lI
> 

This is really a great find !!!!

The result is truly stunning.

For a small number of points, the difference is not obvious. Above about
200 points, there's a really big difference which becomes more and more
apparent as the population increases.


Thanks for the link Bill.



-- 
Kurtz le pirate
Compagnie de la Banquise

Post a reply to this message

Attachments:
Download 'randompointsincircle.jpg' (216 KB)

Preview of image 'randompointsincircle.jpg'