|
 |
"Mr" <m******r******at_hotmail_dot_fr> wrote:
> "Bald Eagle" <cre### [at] netscape net> wrote:
> > Using the same parameters that were calculated to obtain the First and Second
> > Fundamental Forms of the surface, the mean curvature can be mapped to the
> > surface as well.
>
> Could possible use of this if generalized be ? ...
>
> dirt maps,
> wear maps,
> AO maps,
> clay shaders,
Well, it's just an extension of the spline/surface matching that I was doing for
the monograph to make sure everything flows from one spline/surface to another
smoothly - and there are many levels of "smoothness".
Sometimes referred to as "fairing of a surface", techically referred to as C0,
C1, C2, ... and G0, G1, G2 ....
As for what its other possible us is, you know how we roll around here. People
might adapt it to anything they might think of.
> https://www.shadertoy.com/view/fsGXzc
>
> how does it differ from current AOI ?
AOI is just the angle between the surface normal and the camera
position-to-look-at vector. This is a function pattern that calculates the
curvature of the surface at every vertex (point) of a Bezier patch, given the 16
control points. It answers the (perhaps unasked) question, "How tightly is this
surface curled or dimpled?"
> Is it able to reach further object space angles?
Er..... I dunno.
Digging about in the archives of my HDD and the forums, I answered my question
about using uv maps and regular textures on the same object - clipka said that
was not currently possible. :(
I also re-answered my question about using the slope pattern in functions - it
can't be done, because it always returns zero, since it only truly gets
implemented and assigned values once it gets applied to the surface of an
object, under-the-hood.
I also found my re-write of TOK's VPerp_To_Vector macro, which had something to
do with Kenneth and greebles, but in typical fashion, I can't find the original
thread that started all of that.
So, it _might_ be able to be generalized, but it would be (yet another)
source-code level thing - so maybe Jerome Grimbert or Bill Pokorny could make it
happen in their respective forks.
Aside from that, I'm thinking that it could work sort of like the way you've
made carpets from image maps - we'd feed an object into a macro, and build a
surface in a piecewise fashion based on that. The only way I can currently see
doing that is using trace ().
I have a scene where I can plot the entire Frenet-Serret frame for all the
points on a Bezier surface just using trace (), but at the the moment, the
results are probably only valid because the points are on an axis-aligned grid.
The 2 vectors perpendicular to the normal give me the tangent and binormal,
which I'm treating as du and dv, and I'm assuming that a normalized vector
addition of those will give me duv. I still need the second partial derivatives
to get the curvature - and I have no real idea how to get that numerically or
geometrically except to do a sort of central differences type thing to assess
the concavity/convexity at each point.
No idea if any of that will work, but in typical fashion, I'll just plow ahead
like a blind bull in a china shop, and see what else I can break. :D
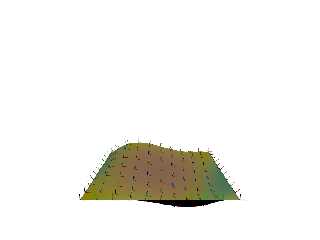
Attached is my WIP, with the surface texture an average of the x y and z slope
{} patterns, which I was naively hoping to use to encode the surface normal in a
function.
The stock VPerp_To_Vector gave me tangents and binormals pointing every which
way, but the rewrite made them all line up consistently. net> wrote:
> > Using the same parameters that were calculated to obtain the First and Second
> > Fundamental Forms of the surface, the mean curvature can be mapped to the
> > surface as well.
>
> Could possible use of this if generalized be ? ...
>
> dirt maps,
> wear maps,
> AO maps,
> clay shaders,
Well, it's just an extension of the spline/surface matching that I was doing for
the monograph to make sure everything flows from one spline/surface to another
smoothly - and there are many levels of "smoothness".
Sometimes referred to as "fairing of a surface", techically referred to as C0,
C1, C2, ... and G0, G1, G2 ....
As for what its other possible us is, you know how we roll around here. People
might adapt it to anything they might think of.
> https://www.shadertoy.com/view/fsGXzc
>
> how does it differ from current AOI ?
AOI is just the angle between the surface normal and the camera
position-to-look-at vector. This is a function pattern that calculates the
curvature of the surface at every vertex (point) of a Bezier patch, given the 16
control points. It answers the (perhaps unasked) question, "How tightly is this
surface curled or dimpled?"
> Is it able to reach further object space angles?
Er..... I dunno.
Digging about in the archives of my HDD and the forums, I answered my question
about using uv maps and regular textures on the same object - clipka said that
was not currently possible. :(
I also re-answered my question about using the slope pattern in functions - it
can't be done, because it always returns zero, since it only truly gets
implemented and assigned values once it gets applied to the surface of an
object, under-the-hood.
I also found my re-write of TOK's VPerp_To_Vector macro, which had something to
do with Kenneth and greebles, but in typical fashion, I can't find the original
thread that started all of that.
So, it _might_ be able to be generalized, but it would be (yet another)
source-code level thing - so maybe Jerome Grimbert or Bill Pokorny could make it
happen in their respective forks.
Aside from that, I'm thinking that it could work sort of like the way you've
made carpets from image maps - we'd feed an object into a macro, and build a
surface in a piecewise fashion based on that. The only way I can currently see
doing that is using trace ().
I have a scene where I can plot the entire Frenet-Serret frame for all the
points on a Bezier surface just using trace (), but at the the moment, the
results are probably only valid because the points are on an axis-aligned grid.
The 2 vectors perpendicular to the normal give me the tangent and binormal,
which I'm treating as du and dv, and I'm assuming that a normalized vector
addition of those will give me duv. I still need the second partial derivatives
to get the curvature - and I have no real idea how to get that numerically or
geometrically except to do a sort of central differences type thing to assess
the concavity/convexity at each point.
No idea if any of that will work, but in typical fashion, I'll just plow ahead
like a blind bull in a china shop, and see what else I can break. :D
Attached is my WIP, with the surface texture an average of the x y and z slope
{} patterns, which I was naively hoping to use to encode the surface normal in a
function.
The stock VPerp_To_Vector gave me tangents and binormals pointing every which
way, but the rewrite made them all line up consistently.
Post a reply to this message
Attachments:
Download 'surfacepropertiespattern.png' (68 KB)
Preview of image 'surfacepropertiespattern.png'
|
 |




![]()