POV-Ray: Newsgroups: povray.off-topic: Another probability question

POV-Ray : Newsgroups : povray.off-topic : Another probability question		Server Time 4 Sep 2024 15:16:55 EDT (-0400)

<<< Previous 6 Messages

Goto Initial 10 Messages

From: Orchid XP v8
Subject: Re: Another probability question
Date: 8 Feb 2010 14:04:43
Message: <4b70604b$1@news.povray.org>

Warp wrote:

>   However, suppose that you use a variant of this: Throw two d10's and
> then the larger result is always used as the tens, and the other as the
> ones.
> 
>   What is the probability distribution now?

Pr(0) = 1/100
Pr(1) = 0/100
Pr(2) = 0/100
Pr(3) = 0/100
Pr(4) = 0/100
Pr(5) = 0/100
Pr(6) = 0/100
Pr(7) = 0/100
Pr(8) = 0/100
Pr(9) = 0/100
Pr(10) = 2/100
Pr(11) = 1/100
Pr(12) = 0/100
Pr(13) = 0/100
Pr(14) = 0/100
Pr(15) = 0/100
Pr(16) = 0/100
Pr(17) = 0/100
Pr(18) = 0/100
Pr(19) = 0/100
Pr(20) = 2/100
Pr(21) = 2/100
Pr(22) = 1/100
Pr(23) = 0/100
Pr(24) = 0/100
Pr(25) = 0/100
Pr(26) = 0/100
Pr(27) = 0/100
Pr(28) = 0/100
Pr(29) = 0/100
Pr(30) = 2/100
Pr(31) = 2/100
Pr(32) = 2/100
Pr(33) = 1/100
Pr(34) = 0/100
Pr(35) = 0/100
Pr(36) = 0/100
Pr(37) = 0/100
Pr(38) = 0/100
Pr(39) = 0/100
Pr(40) = 2/100
Pr(41) = 2/100
Pr(42) = 2/100
Pr(43) = 2/100
Pr(44) = 1/100
Pr(45) = 0/100
Pr(46) = 0/100
Pr(47) = 0/100
Pr(48) = 0/100
Pr(49) = 0/100
Pr(50) = 2/100
Pr(51) = 2/100
Pr(52) = 2/100
Pr(53) = 2/100
Pr(54) = 2/100
Pr(55) = 1/100
Pr(56) = 0/100
Pr(57) = 0/100
Pr(58) = 0/100
Pr(59) = 0/100
Pr(60) = 2/100
Pr(61) = 2/100
Pr(62) = 2/100
Pr(63) = 2/100
Pr(64) = 2/100
Pr(65) = 2/100
Pr(66) = 1/100
Pr(67) = 0/100
Pr(68) = 0/100
Pr(69) = 0/100
Pr(70) = 2/100
Pr(71) = 2/100
Pr(72) = 2/100
Pr(73) = 2/100
Pr(74) = 2/100
Pr(75) = 2/100
Pr(76) = 2/100
Pr(77) = 1/100
Pr(78) = 0/100
Pr(79) = 0/100
Pr(80) = 2/100
Pr(81) = 2/100
Pr(82) = 2/100
Pr(83) = 2/100
Pr(84) = 2/100
Pr(85) = 2/100
Pr(86) = 2/100
Pr(87) = 2/100
Pr(88) = 1/100
Pr(89) = 0/100
Pr(90) = 2/100
Pr(91) = 2/100
Pr(92) = 2/100
Pr(93) = 2/100
Pr(94) = 2/100
Pr(95) = 2/100
Pr(96) = 2/100
Pr(97) = 2/100
Pr(98) = 2/100
Pr(99) = 1/100

You can compute this quite easily in Haskell:

numbers = do
   a <- [0..9]
   b <- [0..9]
   let x = max a b
   let y = min a b
   return (10*x + y)

This tries every possible combination of D10 scores, and builds a list 
of the resulting score.

histogram =
   map (\xs -> (head xs, length xs)) $
   group $
   sort numbers

This sorts the above list, groups equal elements into little sublist, 
and then counts the length of all such sublists, producing a histogram 
chart for all scores with non-zero frequency.

With a little extra trickery and some formatting, you can create the 
above chart.

-- 
http://blog.orphi.me.uk/
http://www.zazzle.com/MathematicalOrchid*

Post a reply to this message

From: Orchid XP v8
Subject: Re: Another probability question
Date: 8 Feb 2010 14:08:03
Message: <4b706113$1@news.povray.org>

Orchid XP v8 wrote:

> You can compute this quite easily in Haskell:

...and yet, an exhaustive analysis of the data quickly demonstrates that 
Andrel was correct in the first place:

Pr(X > Y) = 2/100
Pr(X = Y) = 1/100
Pr(X < Y) = 0/100

-- 
http://blog.orphi.me.uk/
http://www.zazzle.com/MathematicalOrchid*

Post a reply to this message

From: Warp
Subject: Re: Another probability question
Date: 8 Feb 2010 14:13:01
Message: <4b70623c@news.povray.org>

It might be more interesting and intuitive (especially when considering
the original subject matter, ie. throwing dice in a tabletop game) if the
probabilities were divided into ranges. For example, what is the
probability of getting a value in the range 1-10, the range 11-20, the
range 21-30 and so on.

  This distribution ought to be uneven.

-- 
                                                          - Warp

Post a reply to this message

From: andrel
Subject: Re: Another probability question
Date: 8 Feb 2010 14:42:35
Message: <4B70692C.6000100@hotmail.com>

On 8-2-2010 20:04, Orchid XP v8 wrote:
> Warp wrote:
> 
>>   However, suppose that you use a variant of this: Throw two d10's and
>> then the larger result is always used as the tens, and the other as the
>> ones.
>>
>>   What is the probability distribution now?
> 
> Pr(0) = 1/100
> Pr(1) = 0/100
> Pr(2) = 0/100
> Pr(3) = 0/100
> Pr(4) = 0/100
> Pr(5) = 0/100
> Pr(6) = 0/100
> Pr(7) = 0/100
> Pr(8) = 0/100
> Pr(9) = 0/100
> Pr(10) = 2/100
> Pr(11) = 1/100
> Pr(12) = 0/100
> Pr(13) = 0/100
> Pr(14) = 0/100
> Pr(15) = 0/100
> Pr(16) = 0/100
> Pr(17) = 0/100
> Pr(18) = 0/100
> Pr(19) = 0/100
> Pr(20) = 2/100
> Pr(21) = 2/100
> Pr(22) = 1/100
> Pr(23) = 0/100
> Pr(24) = 0/100
> Pr(25) = 0/100
> Pr(26) = 0/100
> Pr(27) = 0/100
> Pr(28) = 0/100
> Pr(29) = 0/100
> Pr(30) = 2/100
> Pr(31) = 2/100
> Pr(32) = 2/100
> Pr(33) = 1/100
> Pr(34) = 0/100
> Pr(35) = 0/100
> Pr(36) = 0/100
> Pr(37) = 0/100
> Pr(38) = 0/100
> Pr(39) = 0/100
> Pr(40) = 2/100
> Pr(41) = 2/100
> Pr(42) = 2/100
> Pr(43) = 2/100
> Pr(44) = 1/100
> Pr(45) = 0/100
> Pr(46) = 0/100
> Pr(47) = 0/100
> Pr(48) = 0/100
> Pr(49) = 0/100
> Pr(50) = 2/100
> Pr(51) = 2/100
> Pr(52) = 2/100
> Pr(53) = 2/100
> Pr(54) = 2/100
> Pr(55) = 1/100
> Pr(56) = 0/100
> Pr(57) = 0/100
> Pr(58) = 0/100
> Pr(59) = 0/100
> Pr(60) = 2/100
> Pr(61) = 2/100
> Pr(62) = 2/100
> Pr(63) = 2/100
> Pr(64) = 2/100
> Pr(65) = 2/100
> Pr(66) = 1/100
> Pr(67) = 0/100
> Pr(68) = 0/100
> Pr(69) = 0/100
> Pr(70) = 2/100
> Pr(71) = 2/100
> Pr(72) = 2/100
> Pr(73) = 2/100
> Pr(74) = 2/100
> Pr(75) = 2/100
> Pr(76) = 2/100
> Pr(77) = 1/100
> Pr(78) = 0/100
> Pr(79) = 0/100
> Pr(80) = 2/100
> Pr(81) = 2/100
> Pr(82) = 2/100
> Pr(83) = 2/100
> Pr(84) = 2/100
> Pr(85) = 2/100
> Pr(86) = 2/100
> Pr(87) = 2/100
> Pr(88) = 1/100
> Pr(89) = 0/100
> Pr(90) = 2/100
> Pr(91) = 2/100
> Pr(92) = 2/100
> Pr(93) = 2/100
> Pr(94) = 2/100
> Pr(95) = 2/100
> Pr(96) = 2/100
> Pr(97) = 2/100
> Pr(98) = 2/100
> Pr(99) = 1/100
> 
> You can compute this quite easily in Haskell:
> 
> numbers = do
>   a <- [0..9]
>   b <- [0..9]
>   let x = max a b
>   let y = min a b
>   return (10*x + y)
> 
> This tries every possible combination of D10 scores, and builds a list 
> of the resulting score.
> 
> histogram =
>   map (\xs -> (head xs, length xs)) $
>   group $
>   sort numbers
> 
> This sorts the above list, groups equal elements into little sublist, 
> and then counts the length of all such sublists, producing a histogram 
> chart for all scores with non-zero frequency.
> 
> With a little extra trickery and some formatting, you can create the 
> above chart.
>

Post a reply to this message

Attachments:
Download 'warp.png' (9 KB)

Preview of image 'warp.png'

From: andrel
Subject: Re: Another probability question
Date: 8 Feb 2010 14:43:45
Message: <4B706972.1050709@hotmail.com>

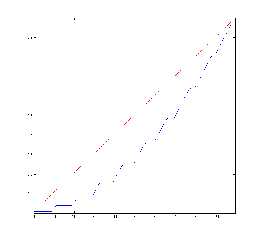
On 8-2-2010 20:08, Orchid XP v8 wrote:
> Orchid XP v8 wrote:
> 
>> You can compute this quite easily in Haskell:
> 
> ...and yet, an exhaustive analysis of the data quickly demonstrates that 
> Andrel was correct in the first place:
> 
> Pr(X > Y) = 2/100
> Pr(X = Y) = 1/100
> Pr(X < Y) = 0/100
> 

exhaustive analysis? What exhaustive analysis?

Post a reply to this message

From: Orchid XP v8
Subject: Re: Another probability question
Date: 8 Feb 2010 15:47:29
Message: <4b707861@news.povray.org>

>>> You can compute this quite easily in Haskell:
>>
>> ...and yet, an exhaustive analysis of the data quickly demonstrates 
>> that Andrel was correct in the first place:
>>
>> Pr(X > Y) = 2/100
>> Pr(X = Y) = 1/100
>> Pr(X < Y) = 0/100
>>
> 
> exhaustive analysis? What exhaustive analysis?

Reading the entire dataset by hand - the brute-force approach. ;-)

-- 
http://blog.orphi.me.uk/
http://www.zazzle.com/MathematicalOrchid*

Post a reply to this message

From: andrel
Subject: Re: Another probability question
Date: 8 Feb 2010 15:55:14
Message: <4B707A32.2080004@hotmail.com>

On 8-2-2010 21:47, Orchid XP v8 wrote:
>>>> You can compute this quite easily in Haskell:
>>>
>>> ...and yet, an exhaustive analysis of the data quickly demonstrates 
>>> that Andrel was correct in the first place:
>>>
>>> Pr(X > Y) = 2/100
>>> Pr(X = Y) = 1/100
>>> Pr(X < Y) = 0/100
>>>
>>
>> exhaustive analysis? What exhaustive analysis?
> 
> Reading the entire dataset by hand - the brute-force approach. ;-)

Ok, I'll make a note of that. If ever I have the pleasure to interview 
you for a job, I will pull that from my pocket.

Post a reply to this message

From: Paul Fuller
Subject: Re: Another probability question
Date: 8 Feb 2010 22:18:01
Message: <4b70d3e9$1@news.povray.org>

On 9/02/2010 06:13 AM, Warp wrote:
>    It might be more interesting and intuitive (especially when considering
> the original subject matter, ie. throwing dice in a tabletop game) if the
> probabilities were divided into ranges. For example, what is the
> probability of getting a value in the range 1-10, the range 11-20, the
> range 21-30 and so on.
>
>    This distribution ought to be uneven.
>

Your rule 'folds' some of the values into others.  Visualise this as a 
10 x 10 table.  Each cell has the starting probability of 1 / 100.  The 
axis where D1 = D2 (10 cells) remains unaffected.  The cells from one 
triangle off the axis get turned to 0 and their previous value added to 
the cell reflected across the axis.  So these all become probability 2 / 
100.

There are 10 cases where D1 = D2, 45 where D1 < D2 and 45 where D1 > D2.

Lets say you fold the D1 < D2 cases into D1 > D2 by reversing the order 
of the digits.

Now there are 10 cases (unchanged) where D1' = D2' each with probability 
1 / 100 and 45 cases where D1' > D2' each with probability 2 / 100.

Considering the ranges:

- I'm going to use the range 00-99 because it makes things easier to set 
out.  Just add 1 to map it to 1-100.
- Each 'decade' has one of the D1' = D2' cases.  The first decade (ie 
00-09) has no case where D1' > D2'.
- Each subsequent decade has one more case where D1' > D2' than the 
previous decade.

To set that out:

P(00-99) = (1 / 100 + (0 * 2 / 100)) = 1 / 100
P(10-19) = (1 / 100 + (1 * 2 / 100)) = 3 / 100
P(20-29) = (1 / 100 + (2 * 2 / 100)) = 5 / 100
...
P(n0-n9) = (1 / 100 + (n * 2 / 100)) = (1 + 2n) / 100
...
P(90-99) = (1 / 100 + (9 * 2 / 100)) = 19 / 100

Summing 1 + 3 + 5 ... + 19 = 100 just to confirm.

And graphing the cumulative values gives Andrel's chart.

Note that summing the sequence 1, 3, ... (1 + 2n) gives the value n^2. 
Thus the curve is parabolic.  Or at least the step up at the end of each 
decade sits on a parabola.   The intermediate steps track along flat or 
step up at 45 degrees. to get to that point.

Post a reply to this message

From: Paul Fuller
Subject: Re: Another probability question
Date: 8 Feb 2010 22:30:56
Message: <4b70d6f0$1@news.povray.org>

> Note that summing the sequence 1, 3, ... (1 + 2n) gives the value n^2.
> Thus the curve is parabolic. Or at least the step up at the end of each
> decade sits on a parabola. The intermediate steps track along flat or
> step up at 45 degrees. to get to that point.

Correction:

That last term should be (2n - 1) rather than (1 + 2n).

Post a reply to this message

From: scott
Subject: Re: Another probability question
Date: 9 Feb 2010 02:55:05
Message: <4b7114d9@news.povray.org>

>> any multiple of 11 has a probability of 1/100.
>> if the numbers are not the same the one where the 10 has a higher value
>> than the 1 has a probability of 2/100. the rest has probability 0
>
>  But getting values eg. in the range 10-20 is a lot less probable than
> getting values in the range 80-90. This would suggest that the probability
> distribution is not very even.

Well yes, because as andrel said, numbers where the unit is higher than the 
ten have a probability of 0.

So in 10-19 the only numbers you can get are 10 (P=2/100) and 11 (P=1/100) - 
overall P=3/100

whereas in 80-89 you can get 80-88, total P=9/100.

So you're 3 times more likely to get a number in the range 80-89 as you are 
10-19.

Post a reply to this message

<<< Previous 6 Messages

Goto Initial 10 Messages