|
 |
Following up on the 3D and 2D SDF functions from Inigo Quilez' articles, I added
macros to my libisosurfaces.inc library to implement his SDF duplication
functions in SDL. (https://github.com/carath63/povlibrary)
So far I have only implemented the 2D duplication functions in the XZ plane.
The basic process to use this is to define an SDF for the shape in each cell of
the grid. There are then macros that define the isosurface function for the
whole grid in various flavors.
To allow the cell SDFs to generate variant shapes across cells, those functions
are defined as a function(x,y,z,cx,cz,idx,idz) where:
x,y,z are the relative coordinates of a point within a given cell
cx,cz are the size of a cell in the XZ plane
idx,idz are the indices of the cell
If you want the same object in all cells, your function just ignores
cx,cz,idx,idz. In this example, the shape is an Iso_sphere() scaled in the
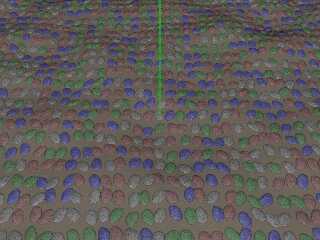
x,y,z directions to look like a flat stone. The dimensions of the stone are
based on the cell size (cx,cz) and noise functions that I call with
(idx*cx,0,idz*cz). I add further noise to get the rough edges of the stone
based on idx*cx+x, and idz*cz+z. I also generate a random rotation for each
stone based on idx and idz, as well as random translations of the stone within
the cell. As you can see this sometimes causes stones to overlap, which I
haven't bothered to try and fix.
The other part of this is creating a texture for the isosurface such that
individual stones have a consistent texture. There are equivalent macros for
creating grid textures. As you can see in the image, even in places where a
stone crosses the boundary of another cell, its texture remains consistent.
For this particular image I also did a translation along the Y axis based on a
terrain heightfield and then created the "sand" object from that same
heightfield so the stones have something interesting to rest on.
If you look at the code at all, you will see that there is a family of these
functions labeled "inexact" and "exact". The difference between these is that
for the inexact, once you determine the cell within which a particular point
lies, you only call the shape SDF based on the point's offset within that cell.
If you have objects that can overlap into other cells, this can cause those
objects to be cut off along the cell line. The "exact" versions of the macros
take this into account, and for each point, it finds the 3 neighboring cells
along the same quadrant as the point within the cell and returns the minimum SDF
value across the cell and its neighbors.
There are also "limited" versions of the functions. These are provided to
enable fixed-size grids, and ensure that points outside of the boundaries of the
grid are considered to be part of the outer cells, rather than new cells. It
prevents having partial objects cut along sharp boundaries of the isosurfaces.
The base versions of these grid functions take the standard x,y,z arguments, but
also included cx,cz to define the cell size, and for the limited functions they
include gx,gz for the grid size (number of cells in the grid). I haven't played
around with what happens if you call these functions with varying cell or grid
sizes. I assume it's probably a mess. I did this mainly for some other
examples I put together where each cell of a grid was itself a grid, and the
number of cells in those sub-grids could vary, (so you could have one cell in
the outer grid that has only one object in it, but another cell could be 2x2 or
3x3, etc.). If you are not doing recursive grids, there are versions of the
macros with "fixedlimited" and/or "fixedcell" that fix the grid and cell size,
giving you a function(x,y,z) that you can use directly in an isosurface
function.
-- Chris R.
Post a reply to this message
Attachments:
Download 'pebbles.png' (1193 KB)
Preview of image 'pebbles.png'
|
 |




![]()