|
 |
In some of my pov-projects I came up with a helpful way of manipulating objects
- something I call "nonlinear scaling". For instance, when I have an upright
cylinder and I want to make it "wavy", I would set the x- and z-scaling to
depend on the y-coordinate. Here's a code snippet:
#declare slicecount = 0;
#declare delta_y = .01;
#while (slicecount < 5)
intersection{
cylinder{<0,0,0>,<0,5,0>,1 pigment{rgb <0,1,.5>}}
box{<-2,0,-2>,<2,delta_y,2> pigment{rgb <0,1,.5>}translate y*slicecount}
scale<sin(slicecount*5)/3+2/3,1,sin(slicecount*5)/3+2/3>}
#declare slicecount = slicecount + delta_y;
#end
If you render this, you see the original cylinder{<0,0,-3>,<0,5,-3>,1
pigment{rgb <0,.5,1>}} was transformed just as I wanted. I could use any
arbitrary function for scaling in any direction. Okay, I could use some
isosurface with this, bun once you exchange the cylinder with a larger csg this
is no longer an option.
Why "feature request"? If you render the above, you will see black artifacts on
the cylinder. Even increasing delta_y to ever so minute amounts will not
eliminate these (but parsing times soar). So it would be neat-o if there were
some way of "optimizing" that, just like the difference between placing a
million spheres and the sphere sweep.
Alternatively, is there any other way to achieve something like this? Or maybe
reduce the spots? I am aware that povray programm(ing/er) time is scarce and
precious, but maybe somebody has a flash of genius :) Or just share your
thoughts on this.
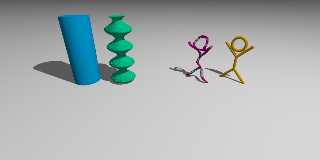
Attached is the image for the following code:
camera{location<20,10,0>*.6 look_at <0,0,0> right x*2}
light_source{<10,20,10> rgb <1,1,1>}
plane{y,0 pigment {rgb 1}}
cylinder{<0,0,-6>,<0,5,-6>,1 pigment{rgb <0,.5,1>}}
#declare slicecount = 0;
#declare delta_y = .01;
#while (slicecount < 5)
intersection{
cylinder{<0,0,0>,<0,5,0>,1 pigment{rgb <0,1,.5>}}
box{<-2,0,-2>,<2,delta_y,2> pigment{rgb <0,1,.5>}translate y*slicecount}
scale<sin(slicecount*5)/3+2/3,1,sin(slicecount*5)/3+2/3> translate z*-3}
#declare slicecount = slicecount + delta_y;
#end
#declare c1 = <0,0,-1>;
#declare c2 = <0,0,1>;
#declare c3 = <0,1,0>;
#declare c4 = <0,2,0>;
#declare c5 = <0,3,-1>;
#declare c6 = <0,3,1>;
#declare stickguy = union{
cylinder{c1,c3,.1}
cylinder{c2,c3,.1}
cylinder{c3,c4,.1}
cylinder{c4,c5,.1}
cylinder{c4,c6,.1}
torus{.5,.1 rotate z*90 translate y*3}}
object{stickguy pigment{rgb <1,.5,0>} rotate y*45 translate z*6}
#declare slicecount_2 = 0;
#declare delta_y_2 = .05;
#while (slicecount_2 < 5)
intersection{
object{stickguy pigment{rgb <1,0,.5>}}
box{<-2,0,-2>,<2,delta_y_2,2> pigment{rgb <0,1,.5>}translate y*slicecount_2}
translate x*1 scale<sin(slicecount_2*5)/4+.75,1,1> translate x*-1 rotate y*45
translate z*3}
#declare slicecount_2 = slicecount_2 + delta_y_2;
#end
Post a reply to this message
Attachments:
Download 'nonlin2.png' (38 KB)
Preview of image 'nonlin2.png'
|
 |
|
 |
Warp <war### [at] tag povray povray org> wrote:
> MDenham <nomail@nomail> wrote:
> > Rather, if there was an easy way of performing _arbitrary_ non-linear
> > transformations on arbitrary surfaces. (Throwing in simple polynomial
> > transforms should be reasonably feasible, however; I'll see if I can hash
> > something up to try it out here sometime in the next few weeks.)
>
> No, it's just not possible to perform *any* non-linear transformations
> to arbitrary surfaces. Not in any efficient and accurate way.
>
> The reason is that non-linear transformations (ie. those which cannot
> be expressed with a 4x4 transformation matrix) would require curved rays
> to raytrace, and that's just not feasible.
>
> --
> - Warp
It's possible to do it without using curved rays, actually; the problem is that,
for meshes, it turns into "take a triangle-like section of a polynomial surface
for every triangle in the mesh", which is (1) ugly to code (2) slow (3) not
possible to improve (unfortunately). For everything else, it turns into
"substitute these polynomials for the coordinates, then re-solve"; this is also
slower, but somewhat more reasonable. It is, essentially, the equivalent of
"convert everything that uses polynomial transforms to an isosurface", only
automatic. Since all of the primitives, except mesh/mesh2, can be represented
fairly easily as an equation, or a relatively small set of equations, this
method should be reasonable to implement. org> wrote:
> MDenham <nomail@nomail> wrote:
> > Rather, if there was an easy way of performing _arbitrary_ non-linear
> > transformations on arbitrary surfaces. (Throwing in simple polynomial
> > transforms should be reasonably feasible, however; I'll see if I can hash
> > something up to try it out here sometime in the next few weeks.)
>
> No, it's just not possible to perform *any* non-linear transformations
> to arbitrary surfaces. Not in any efficient and accurate way.
>
> The reason is that non-linear transformations (ie. those which cannot
> be expressed with a 4x4 transformation matrix) would require curved rays
> to raytrace, and that's just not feasible.
>
> --
> - Warp
It's possible to do it without using curved rays, actually; the problem is that,
for meshes, it turns into "take a triangle-like section of a polynomial surface
for every triangle in the mesh", which is (1) ugly to code (2) slow (3) not
possible to improve (unfortunately). For everything else, it turns into
"substitute these polynomials for the coordinates, then re-solve"; this is also
slower, but somewhat more reasonable. It is, essentially, the equivalent of
"convert everything that uses polynomial transforms to an isosurface", only
automatic. Since all of the primitives, except mesh/mesh2, can be represented
fairly easily as an equation, or a relatively small set of equations, this
method should be reasonable to implement.
Post a reply to this message
|
 |
|
 |
MDenham <nomail@nomail> wrote:
> Since all of the primitives, except mesh/mesh2, can be represented
> fairly easily as an equation, or a relatively small set of equations, this
> method should be reasonable to implement.
Meshes are not the only problematic primitives.
Besides height_field (rather obviously, as it's just a "disguised" mesh),
you also have the julia_fractal object, which is traced iteratively rather
than solving an equation.
Then there are the primitives which are generated using splines, such as
lathe, sor and, I think technically speaking, the text object. While you
probably can express the splines as single polynomials (rather than a group
of polynomials as splines usually are solved), they probably become really
complicated for larger splines. It might be possible to create specialized
code for transforming spline-based objects, though.
Then there are the infinite surfaces, which do not present problems
from the transformation point of view per se, but from the raytracing
point of view. Rather ironically, the poly object might be hard to
transform freely if the poly object represents an infinite surface:
Yes, you can calculate the transformed equation, but how will you
trace it? Isosurfaces always need some boundaries to be traced. Only
if the transformed poly object is another valid poly object, it becomes
possible.
--
- Warp
Post a reply to this message
|
 |




![]()