|
 |
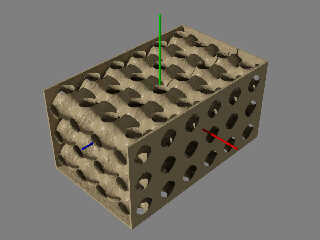
In newusers there was recently a post about creating an isosurface with
the function "cos(x) + cos(y) + cos(z)". I decided to grab that function
and play with the new to povr fork's f_boxb(). A function intended for
use in specifically with isosurfaces.
f_boxb() is a function which takes another function as an input and
encloses it in a box which in part or in total is expected to be smaller
than the isosurface contained_by shape.
The contained_by shape can itself be used to clip away sides of the now
boxed original function to expose an inner structure. I did this on the
top and front in the attached image.
Bill P.
Aside: The gradient of "cos(x) + cos(y) + cos(z)" is relatively high as
isosurface functions go.
// Code ONLY works with the povr fork
...
#include "functions.inc"
// Function f_boxb defined in functions.inc
#declare Fn03 = function (x,y,z) { (cos(x) + cos(y) + cos(z))*-1 }
#declare Fn04 = function (x,y,z) {
f_boxb(x,y,z,0.6,0.667,1,-0.02,0,0,Fn03(x*20,y*20,z*20),0.010)
}
#declare Iso99 = isosurface {
function { Fn04(x,y,z) }
contained_by { box { <-1,-1,-0.95>,<1,1/3,1> } }
threshold 0
accuracy 0.00017
max_gradient 33.3
}
#declare SorrellBrown = srgb <0.80784,0.72549,0.56078>;
#declare Pigment02 = pigment { color SorrellBrown }
#declare Normal02 = normal { granite 0.31 scale 0.177 }
#declare Finish02 = finish { phong 0.33 }
#declare Texture02 = texture {
pigment { Pigment02 }
finish { Finish02 }
normal { Normal02 }
}
#declare Obj02 = object { Iso99 texture { Texture02 } }
...
Post a reply to this message
Attachments:
Download 'threecosiso.jpg' (108 KB)
Preview of image 'threecosiso.jpg'
|
 |
|
 |
On 2/19/23 14:38, Bald Eagle wrote:
> That looks cool.
Thanks.
>
> Now all you need to do is interlace that function with some white ovoids with
> micronormals, and you sell those by the case for $50+ each.
:-)
---
> Aside: The gradient of "cos(x) + cos(y) + cos(z)" is relatively high
> as isosurface functions go.
Aside to my aside... We can lower the gradient in the above case. By
noticing the function values swing between -3 and 3 in a symmetrical
way, we can code:
#declare Fn03 = function (x,y,z) {
(cos(x) + cos(y) + cos(z))*(1/3)
}
Which re-maps the values to -1 to 1. Why not *1/9 you ask for an even
lower gradient? Well, you can, but it gets to be a gradient game with
isosurfaces after some point. It tends' to help to get everything into a
more common value space - and I aim for -1 to 1 as a rule - as in that
space functions tend to play better together.
Bill P.
Post a reply to this message
|
 |




![]()