 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
For once in my life it looks like I properly interpreted something in
Wikipedia and actually wrote the code to implement the psuedo-code on
their page.
Not only that, but based on what the psuedocode was saying, I properly
surmised how to interpolate the resulting spline functions for each
interval.
Well, of course a spline is easy. Right?
I just wish I knew a bit more of the underlying theory of how the
coefficients were calculated.
The article speaks of derivatives, so calculus must be involved. I'm
gathering that the formulae in the algorithm were probably found by
applying calculus to a 3rd order polynomial.
http://en.wikipedia.org/wiki/Cubic_spline
--
~Mike
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Mike Raiford wrote:
> The article speaks of derivatives, so calculus must be involved. I'm
> gathering that the formulae in the algorithm were probably found by
> applying calculus to a 3rd order polynomial.
>
> http://en.wikipedia.org/wiki/Cubic_spline
Or they were derived by calculating which coefficients will yield
continuity in the first derivative. And maybe the second.
I am presently note-scribbling for a scene-building feature for my
modeler, and I want something that is simple and C2 continuous when the
user specifies continuity at a point. I've decided to use the limit
curves of a subdivided border (end points stay still, new mid points are
the average of the start and end of the edge, and new interior points
are calculated on a 1-6-1 mask). The result is a cubic spline with C0,
C1, and C2 continuity. It does not necessarily pass through the control
points, but I have a work-around for that.
C2 continuity is important in animation; if the two spline ends meet in
the middle of a curve, and the object moving along the curve is tilted
to show its acceleration, then any discontinuity at the join will result
in the sudden change in the tilt of the object. This is usually undesired.
Regards,
John
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 24-2-2009 17:11, Mike Raiford wrote:
> For once in my life it looks like I properly interpreted something in
> Wikipedia and actually wrote the code to implement the psuedo-code on
> their page.
>
> Not only that, but based on what the psuedocode was saying, I properly
> surmised how to interpolate the resulting spline functions for each
> interval.
>
> Well, of course a spline is easy. Right?
>
> I just wish I knew a bit more of the underlying theory of how the
> coefficients were calculated.
>
> The article speaks of derivatives, so calculus must be involved. I'm
> gathering that the formulae in the algorithm were probably found by
> applying calculus to a 3rd order polynomial.
>
> http://en.wikipedia.org/wiki/Cubic_spline
>
>
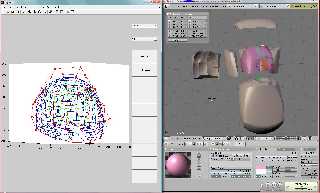
This is what my screen looks ATM. On the left my dedicated bezier volume
editor and in blender a torso of a patient that is subdivided in
deformed cubes. Don't ask.
I prefer Bezier because it gives easy control and it is easy to switch
between control points and actual points on the curve. So when I need to
subdivide a line (or volume) I compute the points where the new line
must go through and convert that back to control points. This gives
absolute smooth transitions between the parts. Around the heart and lung
volumes there are discontinuities that I deliberately introduced, but
you can not see the seams in e.g. the front of the lower body, the lower
part is actually 5 by 4 by 2 blocks of rubber.
Post a reply to this message
Attachments:
Download 'knipsel.jpg' (263 KB)
Preview of image 'knipsel.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Mike Raiford wrote:
> Not only that, but based on what the psuedocode was saying, I properly
> surmised how to interpolate the resulting spline functions for each
> interval.
Nice! Sounds very smooth.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 2/24/2009 1:31 PM, Kevin Wampler wrote:
> Mike Raiford wrote:
>> Not only that, but based on what the psuedocode was saying, I properly
>> surmised how to interpolate the resulting spline functions for each
>> interval.
>
> Nice! Sounds very smooth.
Groan!
--
...Chambers
www.pacificwebguy.com
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
>> Nice! Sounds very smooth.
>
> Groan!
That Curly Phi. He's one smooth operator. ;-)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Mike Raiford wrote:
> Well, of course a spline is easy. Right?
Heh. Not so much... ;-)
> I just wish I knew a bit more of the underlying theory of how the
> coefficients were calculated.
>
> The article speaks of derivatives, so calculus must be involved. I'm
> gathering that the formulae in the algorithm were probably found by
> applying calculus to a 3rd order polynomial.
Suppose you want a line that passes through points A and B. That is, you
want a function f(x) such that
f(0) = A
f(1) = B
That's quite easy to arrange:
f(x) = A(1-x) + Bx
This gives us a straight line between any two points. Notice that we can
rearrange it as:
f(x) = A(1-x) + Bx = A - Ax + Bx = (B-A)x + B
which is your usual "standard form" for a linear equation.
Now, suppose we want a curve going through *three* points, A, B and C?
f(0.0) = A
f(0.5) = B
f(1.0) = C
How do we do that? Well, you can make a function
g(0.0) = A
g(0.5) = B
which gives us g(x) = A(1-2x) + B(2x), and another function
h(0.5) = B
h(1.0) = C
which gives h(x) = B(1-2(x-0.5)) + C(2(x-0.5)). If you sort out all the
coefficients, those are both linear, and you can "blend" between them
like this:
f(x) = (1-x) g(x) + x h(x)
When you sort out all the algebra, you end up with a quadratic curve
passing through all three points, as required. I've found from
experience that this spline isn't very easy to control though!
Part of the reason for that is that if B is higher than A or C, B isn't
necessarily the highest point on the curve. That could be to either side
of B.
The more sophisticated splines are defined by stipulating specific
properties the curve must have. As you have noticed, this has to do with
calculus. In particular, the derivative of a 1D function is the *slope*
of the graph at that point. And the second derivative is the *curvature*
of the graph at that point. Obviously slope and curvature are useful
things to want to control.
For example, take my defective quadratic spline above. I said that B
isn't necessarily the highest point. In fact, if you draw a line AB and
a line BC, you'll discover that the slope of the function doesn't match
either of these lines at any point.
(I should perhaps point out that it's impossible for a quadratic curve
to fit any better than this. Any three points in space uniquely define a
single quadratic curve. For a more controllable curve, you'd need a
higher-order polynomial.)
More sophisticated splines say "I want the slope of the graph to match
the line AB at the start". Since "slope" is actually "first derivative",
you end up using calculus. So you end up with something like
f(0.0) = A
f(0.5) = B
f(1.0) = C
f'(0.0) = B-A
f'(1.0) = C-B
How you can from this system of constraints to a working function is
just slightly beyond by level of skill. But you see where the calculus
comes in...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()