 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> Hopefully this does the trick. I have more curves to plot, and then need to
> adapt my macros to parametrics and then the polynomial curves.
......aaand it's not quite. When the curve is nearly vertical, my select ()
statement hard-codes the Phi to be zero, so maybe I have to do a central
differences type thing and average f(+/-h)
Post a reply to this message
Attachments:
Download 'tubecurves.png' (222 KB)
Preview of image 'tubecurves.png'
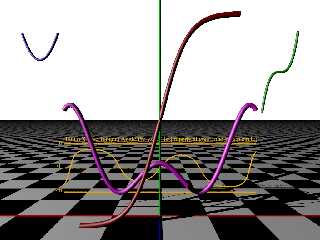
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> > "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> > "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> > > "Bald Eagle" <cre### [at] netscape com> wrote:
> > > "Bald Eagle" <cre### [at] netscape net> wrote:
> > > > "Droj" <803### [at] droj net> wrote:
> > > > "Droj" <803### [at] droj de> wrote:
> > > >
> > > > > > I will try to do some fine tuning as the heart curve still has an
inconsistency
> > > > > > where the dip is.
>
>
> > > My suspicion is that this is caused by a problem with the Paramcalc
> > > macro in meshmaker.inc (The SimpleMesh macro in the code below does
> > > not seem to have this problem.)
> > >
> > > The code below also shows an alternative way to make the final
> > > functions for the "tube".
> > >...
> >
> > I see now that the SimpleMesh macro is a bit messy.
>
> I haven't gone through any of the edited mesh macro code yet, but did some
> simple mesh creation code of my own, and the problem was still in the
> calculation of that damned angle Phi. It's not very well-behaved, and jumps
> around a lot, making adjacent sections of mesh "flip" through the central curve
> trace.
>
> I played around with it for quite a while, graphing the values of Phi, and
> finally came up with this:
>
> #macro Implicit_CalculatePhi (UU, I_Derivative)
> #local Phi = -atan2 (I_Derivative (UU)*UU, abs (UU+E));
> // correct for flipping around x=0
> #local Phi = select ((Phi+pi/2), Phi+pi, Phi);
> #local Phi = select (UU, -Phi, 0, Phi);
>
> Phi
> #end
>
> It keeps Phi as a nice, continuous value between +/-pi
>
> So in the loops, instead of calculating Phi, just use:
> #local Phi = Implicit_CalculatePhi (UU, I_Derivative);
>
> And that seems to have eliminated all of the problems I've noticed at x0 <= 0
> where there are mins and maxes in the curve.
>
> Hopefully this does the trick. I have more curves to plot, and then need to
> adapt my macros to parametrics and then the polynomial curves.
Bill,
I'm worried that maybe you are making things more complicated than they are.
That's because my tests indicate that atan2(DFnY(u), DFnX(u)) does a good job
calculating the angle of the tangent. One just have to add or subtract pi/2 to
get an angle pi/2 (90 degrees) away from the tangent direction (in the
XY-plane).
I'll try to explain...
If we, in order to simplify things, set the tube radius to 1 and pretend
that POV-Ray has 3D-vector valued functions, then the problem can be
solved like this:
X = function(u) { 16*pow(sin(u), 3) }
Y = function(u) { 13*cos(u) - 5*cos(2*u) - 2*cos(3*u) - cos(4*u) }
pCtr = function3d(u) { <X(u), Y(u), 0> }
d_X = function(u) { 48*pow(sin(u), 2)*cos(u) }
d_Y = function(u) { -13*sin(u) + 10*sin(2*u) + 6*sin(3*u) + 4*sin(4*u) }
vTangent = function3d(u) { <d_X(u), d_Y(u), 0> }
TangentAngle = function(u) { atan2(d_Y(u), d_X(u)) }
OrthAngle = function(u) { TangentAngle(u) + pi/2 } // or TangentAngle(u) - pi/2
We need two vectors that are orthogonal to the tangent of the curve,
that is orthogonal to each other and has unit length. Since this is
a 2D curve in an XY-plane, they can be created like this:
vOrth_1a = function3d(u) { <cos(OrthAngle(u)), sin(OrthAngle(u)), 0> }
vOrth_2 = function3d(u) { <0, 0, +1> } // or <0, 0, -1>
All the points on the surface can now be calculated like this:
pSurface =
function3d(u, v) {
pCtr(u) +
cos(v)*vOrth_1a(u) +
sin(v)*vOrth_2(u)
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
cos(v)*<cos(OrthAngle(u)), sin(OrthAngle(u)), 0> +
sin(v)*<0, 0, 1>
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
<cos(v)*cos(OrthAngle(u)), cos(v)*sin(OrthAngle(u)), 0> +
<0, 0, sin(v)>
}
pSurface =
function3d(u, v) {
<
cos(v)*cos(OrthAngle(u)) + X(u),
cos(v)*sin(OrthAngle(u)) + Y(u),
sin(v)
>
}
Here's an alternative way of creating the first orthogonal vector:
vTangentNormalized =
function3d(u) {
<cos(TangentAngle(u)), sin(TangentAngle(u)), 0>
}
vOrth_1b =
function3d(u) {
<-vTangentNormalized(u).y, +vTangentNormalized(u).x, 0>
// or <+vTangentNormalized(u).y, -vTangentNormalized(u).x, 0>
}
vOrth_1b =
function3d(u) {
<-sin(TangentAngle(u)), +cos(TangentAngle(u)), 0>
}
Again the points on the surface can be calculated like this:
pSurface =
function3d(u, v) {
pCtr(u) +
cos(v)*vOrth_1b(u) +
sin(v)*vOrth_2(u)
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
cos(v)*<-sin(TangentAngle(u)), +cos(TangentAngle(u)), 0> +
sin(v)*<0, 0, 1>
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
<cos(v)*-sin(TangentAngle(u)), cos(v)*+cos(TangentAngle(u)), 0> +
<0, 0, sin(v)>
}
pSurface =
function3d(u, v) {
<
-cos(v)*sin(TangentAngle(u)) + X(u),
+cos(v)*cos(TangentAngle(u)) + Y(u),
sin(v)
>
}
The normalized tangent can also be calculated like this:
vTangentNormalized =
function3d(u) {
<d_X(u), d_Y(u), 0>/f_r(d_X(u), d_Y(u), 0)
}
Now we have yet another way to create the first orthogonal vector:
vOrth_1c =
function3d(u) {
<-vTangentNormalized(u).y, +vTangentNormalized(u).x, 0>
// or <+vTangentNormalized(u).y, -vTangentNormalized(u).x, 0>
}
vOrth_1c =
function3d(u) {
<-d_Y(u), +d_X(u), 0>/f_r(d_X(u), d_Y(u), 0)
}
The points on the surface can be calculated like this:
pSurface =
function3d(u, v) {
pCtr(u) +
cos(v)*vOrth_1c(u) +
sin(v)*vOrth_2(u)
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
cos(v)*<-d_Y(u), +d_X(u), 0>/f_r(d_X(u), d_Y(u), 0) +
sin(v)*<0, 0, 1>
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
cos(v)*<-d_Y(u), +d_X(u), 0>/f_r(d_X(u), d_Y(u), 0) +
<0, 0, sin(v)>
}
pSurface =
function3d(u, v) {
<
-cos(v)*d_Y(u)/f_r(d_X(u), d_Y(u), 0) + X(u),
+cos(v)*d_X(u)/f_r(d_X(u), d_Y(u), 0) + Y(u),
sin(v)
>
}
--
Tor Olav
http://subcube.com
https://github.com/t-o-k de> wrote:
> > > >
> > > > > > I will try to do some fine tuning as the heart curve still has an
inconsistency
> > > > > > where the dip is.
>
>
> > > My suspicion is that this is caused by a problem with the Paramcalc
> > > macro in meshmaker.inc (The SimpleMesh macro in the code below does
> > > not seem to have this problem.)
> > >
> > > The code below also shows an alternative way to make the final
> > > functions for the "tube".
> > >...
> >
> > I see now that the SimpleMesh macro is a bit messy.
>
> I haven't gone through any of the edited mesh macro code yet, but did some
> simple mesh creation code of my own, and the problem was still in the
> calculation of that damned angle Phi. It's not very well-behaved, and jumps
> around a lot, making adjacent sections of mesh "flip" through the central curve
> trace.
>
> I played around with it for quite a while, graphing the values of Phi, and
> finally came up with this:
>
> #macro Implicit_CalculatePhi (UU, I_Derivative)
> #local Phi = -atan2 (I_Derivative (UU)*UU, abs (UU+E));
> // correct for flipping around x=0
> #local Phi = select ((Phi+pi/2), Phi+pi, Phi);
> #local Phi = select (UU, -Phi, 0, Phi);
>
> Phi
> #end
>
> It keeps Phi as a nice, continuous value between +/-pi
>
> So in the loops, instead of calculating Phi, just use:
> #local Phi = Implicit_CalculatePhi (UU, I_Derivative);
>
> And that seems to have eliminated all of the problems I've noticed at x0 <= 0
> where there are mins and maxes in the curve.
>
> Hopefully this does the trick. I have more curves to plot, and then need to
> adapt my macros to parametrics and then the polynomial curves.
Bill,
I'm worried that maybe you are making things more complicated than they are.
That's because my tests indicate that atan2(DFnY(u), DFnX(u)) does a good job
calculating the angle of the tangent. One just have to add or subtract pi/2 to
get an angle pi/2 (90 degrees) away from the tangent direction (in the
XY-plane).
I'll try to explain...
If we, in order to simplify things, set the tube radius to 1 and pretend
that POV-Ray has 3D-vector valued functions, then the problem can be
solved like this:
X = function(u) { 16*pow(sin(u), 3) }
Y = function(u) { 13*cos(u) - 5*cos(2*u) - 2*cos(3*u) - cos(4*u) }
pCtr = function3d(u) { <X(u), Y(u), 0> }
d_X = function(u) { 48*pow(sin(u), 2)*cos(u) }
d_Y = function(u) { -13*sin(u) + 10*sin(2*u) + 6*sin(3*u) + 4*sin(4*u) }
vTangent = function3d(u) { <d_X(u), d_Y(u), 0> }
TangentAngle = function(u) { atan2(d_Y(u), d_X(u)) }
OrthAngle = function(u) { TangentAngle(u) + pi/2 } // or TangentAngle(u) - pi/2
We need two vectors that are orthogonal to the tangent of the curve,
that is orthogonal to each other and has unit length. Since this is
a 2D curve in an XY-plane, they can be created like this:
vOrth_1a = function3d(u) { <cos(OrthAngle(u)), sin(OrthAngle(u)), 0> }
vOrth_2 = function3d(u) { <0, 0, +1> } // or <0, 0, -1>
All the points on the surface can now be calculated like this:
pSurface =
function3d(u, v) {
pCtr(u) +
cos(v)*vOrth_1a(u) +
sin(v)*vOrth_2(u)
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
cos(v)*<cos(OrthAngle(u)), sin(OrthAngle(u)), 0> +
sin(v)*<0, 0, 1>
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
<cos(v)*cos(OrthAngle(u)), cos(v)*sin(OrthAngle(u)), 0> +
<0, 0, sin(v)>
}
pSurface =
function3d(u, v) {
<
cos(v)*cos(OrthAngle(u)) + X(u),
cos(v)*sin(OrthAngle(u)) + Y(u),
sin(v)
>
}
Here's an alternative way of creating the first orthogonal vector:
vTangentNormalized =
function3d(u) {
<cos(TangentAngle(u)), sin(TangentAngle(u)), 0>
}
vOrth_1b =
function3d(u) {
<-vTangentNormalized(u).y, +vTangentNormalized(u).x, 0>
// or <+vTangentNormalized(u).y, -vTangentNormalized(u).x, 0>
}
vOrth_1b =
function3d(u) {
<-sin(TangentAngle(u)), +cos(TangentAngle(u)), 0>
}
Again the points on the surface can be calculated like this:
pSurface =
function3d(u, v) {
pCtr(u) +
cos(v)*vOrth_1b(u) +
sin(v)*vOrth_2(u)
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
cos(v)*<-sin(TangentAngle(u)), +cos(TangentAngle(u)), 0> +
sin(v)*<0, 0, 1>
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
<cos(v)*-sin(TangentAngle(u)), cos(v)*+cos(TangentAngle(u)), 0> +
<0, 0, sin(v)>
}
pSurface =
function3d(u, v) {
<
-cos(v)*sin(TangentAngle(u)) + X(u),
+cos(v)*cos(TangentAngle(u)) + Y(u),
sin(v)
>
}
The normalized tangent can also be calculated like this:
vTangentNormalized =
function3d(u) {
<d_X(u), d_Y(u), 0>/f_r(d_X(u), d_Y(u), 0)
}
Now we have yet another way to create the first orthogonal vector:
vOrth_1c =
function3d(u) {
<-vTangentNormalized(u).y, +vTangentNormalized(u).x, 0>
// or <+vTangentNormalized(u).y, -vTangentNormalized(u).x, 0>
}
vOrth_1c =
function3d(u) {
<-d_Y(u), +d_X(u), 0>/f_r(d_X(u), d_Y(u), 0)
}
The points on the surface can be calculated like this:
pSurface =
function3d(u, v) {
pCtr(u) +
cos(v)*vOrth_1c(u) +
sin(v)*vOrth_2(u)
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
cos(v)*<-d_Y(u), +d_X(u), 0>/f_r(d_X(u), d_Y(u), 0) +
sin(v)*<0, 0, 1>
}
pSurface =
function3d(u, v) {
<X(u), Y(u), 0> +
cos(v)*<-d_Y(u), +d_X(u), 0>/f_r(d_X(u), d_Y(u), 0) +
<0, 0, sin(v)>
}
pSurface =
function3d(u, v) {
<
-cos(v)*d_Y(u)/f_r(d_X(u), d_Y(u), 0) + X(u),
+cos(v)*d_X(u)/f_r(d_X(u), d_Y(u), 0) + Y(u),
sin(v)
>
}
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Hi TOK, and Merry Christmas :)
I can follow all of your calculations, and indeed, I'm using many of the same
methods.
But I'm curious if you've applied the results of the calculations to generating
the mesh of the function's tubular envelope.
That's where I've encountered the sticking point. Since I'm creating vertices
of the circles sequentially along the curve, the "ordering" of those vertices
matter when I then loop through them to create my triangles. When there's a
sign change or a sudden plummet to zero, I get a severe twist in the tube at
that point.
Maybe you can render the following equations so that I can see that your methods
work, and I indeed (as always) am making things too complicated. You may have
noticed that I DO have that knack. ;)
#declare Function = function (U) {U*U+1}
#declare Derivative = function (U) {2*U}
#declare Function = function (U) {0.4 * cos (U) * (-pow (U, 2) + 3 ) -1}
#declare Derivative = function (U) {0.4 * (pow (U, 2) - 3 )* sin (U) - 0.8 * U *
cos (U)}
#declare Function = function (U) {U*U*U}
#declare Derivative = function (U) {3*U*U}
hyperbolic tangent
#declare Function = function (U) {4 * (sinh (U) / cosh (U)) + 4}
#declare Derivative = function (U) {pow (1/cosh(U), 2)}
"softsign"
#declare Function = function (U) {8*(U/(abs(U)+1))}
#declare Derivative = function (U) {pow (1/(abs(x)+1), 2)}
I came up with a bit of a hacky solution that seems to work for ALL of these. I
keep track of the Phi value for each circle, and if I'm at x=0, I just use the
value from the previous circle, and I get nice, continuous results.
After calculating Phi, I just invoke:
#local Phi = (abs (UU)<E ? LastPhi : Phi);
Here's hoping you prove me wrong with a super simple solution. :)
- BW
Post a reply to this message
Attachments:
Download 'tubecurves.png' (217 KB)
Preview of image 'tubecurves.png'
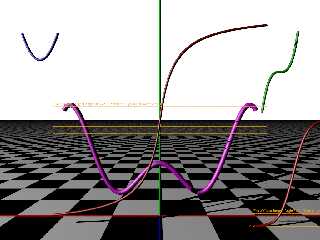
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Hi TOK, and Merry Christmas :)
Thank you Bill =)
Merry Christmas to you too !
> I can follow all of your calculations, and indeed, I'm using many of the same
> methods.
Ok. That's good.
> But I'm curious if you've applied the results of the calculations to generating
> the mesh of the function's tubular envelope.
Yes, I did that. And it looks ok when I'm using my own mesh macro.
But when I use meshmaker.inc it does not look so good.
> That's where I've encountered the sticking point. Since I'm creating vertices
> of the circles sequentially along the curve, the "ordering" of those vertices
> matter when I then loop through them to create my triangles. When there's a
> sign change or a sudden plummet to zero, I get a severe twist in the tube at
> that point.
>
> Maybe you can render the following equations so that I can see that your methods
> work, and I indeed (as always) am making things too complicated. You may have
> noticed that I DO have that knack. ;)
>...
Ok, but please note that Wolfram Alpha does not agree with you on the
derivatives of the last two. Here's how I wrote them:
#declare FnX = function(u) { u };
#declare DFnX = function(u) { 1 };
#declare Fn_Y = array[5];
#declare DFn_Y = array[5];
#declare I = 0;
#declare Fn_Y[I] = function(u) { pow(u, 2) + 1 };
#declare DFn_Y[I] = function(u) { 2*u };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 0.4*cos(u)*(-pow(u, 2) + 3) - 1 };
#declare DFn_Y[I] = function(u) { 0.4*(pow(u, 2) - 3)*sin(u) - 0.8*u*cos(u) };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { u*u*u };
#declare DFn_Y[I] = function(u) { 3*u*u };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 4*sinh(u)/cosh(u) + 4 };
#declare DFn_Y[I] = function(u) { 16*pow(cosh(u), 2)/pow(cosh(2*u) + 1, 2) };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 8*u/(abs(u) + 1) };
#declare DFn_Y[I] = function(u) { 8/pow(abs(u) + 1, 2) };
I ran all these through the SimpleMesh macro. See the attached image for
the results. I can post the complete source for that if you're interested.
> I came up with a bit of a hacky solution that seems to work for ALL of these. I
> keep track of the Phi value for each circle, and if I'm at x=0, I just use the
> value from the previous circle, and I get nice, continuous results.
>
> After calculating Phi, I just invoke:
> #local Phi = (abs (UU)<E ? LastPhi : Phi);
I can not understand why that should be necessary. - But it could be that
it's me that's missing something...
> Here's hoping you prove me wrong with a super simple solution. :)
It's not super simple, but perhaps less complicated ;)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
> Hi TOK, and Merry Christmas :)
Thank you Bill =)
Merry Christmas to you too !
> I can follow all of your calculations, and indeed, I'm using many of the same
> methods.
Ok. That's good.
> But I'm curious if you've applied the results of the calculations to generating
> the mesh of the function's tubular envelope.
Yes, I did that. And it looks ok when I'm using my own mesh macro.
But when I use meshmaker.inc it does not look so good.
> That's where I've encountered the sticking point. Since I'm creating vertices
> of the circles sequentially along the curve, the "ordering" of those vertices
> matter when I then loop through them to create my triangles. When there's a
> sign change or a sudden plummet to zero, I get a severe twist in the tube at
> that point.
>
> Maybe you can render the following equations so that I can see that your methods
> work, and I indeed (as always) am making things too complicated. You may have
> noticed that I DO have that knack. ;)
>...
Ok, but please note that Wolfram Alpha does not agree with you on the
derivatives of the last two. Here's how I wrote them:
#declare FnX = function(u) { u };
#declare DFnX = function(u) { 1 };
#declare Fn_Y = array[5];
#declare DFn_Y = array[5];
#declare I = 0;
#declare Fn_Y[I] = function(u) { pow(u, 2) + 1 };
#declare DFn_Y[I] = function(u) { 2*u };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 0.4*cos(u)*(-pow(u, 2) + 3) - 1 };
#declare DFn_Y[I] = function(u) { 0.4*(pow(u, 2) - 3)*sin(u) - 0.8*u*cos(u) };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { u*u*u };
#declare DFn_Y[I] = function(u) { 3*u*u };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 4*sinh(u)/cosh(u) + 4 };
#declare DFn_Y[I] = function(u) { 16*pow(cosh(u), 2)/pow(cosh(2*u) + 1, 2) };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 8*u/(abs(u) + 1) };
#declare DFn_Y[I] = function(u) { 8/pow(abs(u) + 1, 2) };
I ran all these through the SimpleMesh macro. See the attached image for
the results. I can post the complete source for that if you're interested.
> I came up with a bit of a hacky solution that seems to work for ALL of these. I
> keep track of the Phi value for each circle, and if I'm at x=0, I just use the
> value from the previous circle, and I get nice, continuous results.
>
> After calculating Phi, I just invoke:
> #local Phi = (abs (UU)<E ? LastPhi : Phi);
I can not understand why that should be necessary. - But it could be that
it's me that's missing something...
> Here's hoping you prove me wrong with a super simple solution. :)
It's not super simple, but perhaps less complicated ;)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
Attachments:
Download 'tube_curves.png' (121 KB)
Preview of image 'tube_curves.png'
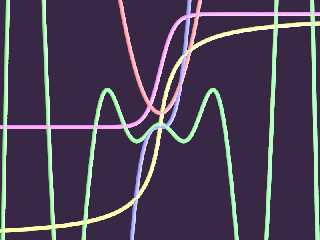
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> I ran all these through the SimpleMesh macro. See the attached image for
> the results. I can post the complete source for that if you're interested.
Yes, that would be interesting to look over.
I'll post my own code here, and maybe you can spot why it's not working with
just a simple Phi calculation.
> I can not understand why that should be necessary. - But it could be that
> it's me that's missing something...
I can only imagine I have some minor error somewhere that gets magnified
later....
All I'm doing is storing the vertices of the tilted circle in a 2D array, and
then moving along the curve and storing those circles. Then I travel around the
stored points in the circle array and make quads with 2 triangles. Standard
stuff. Looks great in the positive quadrant/octant and in the smooth parts of
the negative. So it's odd that it's not working well at specific points, and my
graph of the Phi values was so discontinuous.
Bear in mind that I've only done this for the implicit functions, not 3d the
parametrics. But I should get this sorted out and see what the problem is
before I go any further.
Thanks as always for your clear mind, sharp eyes, and _lightning fast_ code
generation!
- BW com> wrote:
> I ran all these through the SimpleMesh macro. See the attached image for
> the results. I can post the complete source for that if you're interested.
Yes, that would be interesting to look over.
I'll post my own code here, and maybe you can spot why it's not working with
just a simple Phi calculation.
> I can not understand why that should be necessary. - But it could be that
> it's me that's missing something...
I can only imagine I have some minor error somewhere that gets magnified
later....
All I'm doing is storing the vertices of the tilted circle in a 2D array, and
then moving along the curve and storing those circles. Then I travel around the
stored points in the circle array and make quads with 2 triangles. Standard
stuff. Looks great in the positive quadrant/octant and in the smooth parts of
the negative. So it's odd that it's not working well at specific points, and my
graph of the Phi values was so discontinuous.
Bear in mind that I've only done this for the implicit functions, not 3d the
parametrics. But I should get this sorted out and see what the problem is
before I go any further.
Thanks as always for your clear mind, sharp eyes, and _lightning fast_ code
generation!
- BW
Post a reply to this message
Attachments:
Download 'tubecurves.pov.txt' (12 KB)
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>...
> I'll post my own code here, and maybe you can spot why it's not working with
> just a simple Phi calculation.
I have had a thorough look at your code and modified it. You can find it here:
Newsgroup: povray.text.scene-files
Subject: Rewrite of tubecurves.pov (2D function to 3D tube)
Date: 2022-12-27 22:37:15
From: Tor Olav Kristensen
http://news.povray.org/povray.text.scene-files/thread/%3Cweb.63abb9396dfe9e73d6142c8889db30a9%40news.povray.org%3E
> > I can not understand why that should be necessary. - But it could be that
> > it's me that's missing something...
>
> I can only imagine I have some minor error somewhere that gets magnified
> later....
Sorry, but I have not found out exactly where your problem is.
> All I'm doing is storing the vertices of the tilted circle in a 2D array, and
> then moving along the curve and storing those circles. Then I travel around the
> stored points in the circle array and make quads with 2 triangles. Standard
> stuff.
> ...
Yes, that's a sensible way to do it.
>...
> Looks great in the positive quadrant/octant and in the smooth parts of
> the negative. So it's odd that it's not working well at specific points, and my
> graph of the Phi values was so discontinuous.
>
> Bear in mind that I've only done this for the implicit functions, not 3d the
> parametrics. But I should get this sorted out and see what the problem is
> before I go any further.
>
> Thanks as always for your clear mind, sharp eyes, and _lightning fast_ code
> generation!
Hehe, no problem.
I had previously done some work related to this topic; with parametric
functions in 3D, so I already had some code to start with.
If you're interested, you can have a look at the "Trefoil Knot Tube"
example here:
https://github.com/t-o-k/scikit-vectors_examples
https://github.com/t-o-k/scikit-vectors_examples/blob/master/Trefoil_Knot_Tube.pdf
Sometimes GitHub fails to render PDF-files and Jupyter Notbook files (.ipynb).
If that happens, just wait a litte and then try again.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
>...
> I'll post my own code here, and maybe you can spot why it's not working with
> just a simple Phi calculation.
I have had a thorough look at your code and modified it. You can find it here:
Newsgroup: povray.text.scene-files
Subject: Rewrite of tubecurves.pov (2D function to 3D tube)
Date: 2022-12-27 22:37:15
From: Tor Olav Kristensen
http://news.povray.org/povray.text.scene-files/thread/%3Cweb.63abb9396dfe9e73d6142c8889db30a9%40news.povray.org%3E
> > I can not understand why that should be necessary. - But it could be that
> > it's me that's missing something...
>
> I can only imagine I have some minor error somewhere that gets magnified
> later....
Sorry, but I have not found out exactly where your problem is.
> All I'm doing is storing the vertices of the tilted circle in a 2D array, and
> then moving along the curve and storing those circles. Then I travel around the
> stored points in the circle array and make quads with 2 triangles. Standard
> stuff.
> ...
Yes, that's a sensible way to do it.
>...
> Looks great in the positive quadrant/octant and in the smooth parts of
> the negative. So it's odd that it's not working well at specific points, and my
> graph of the Phi values was so discontinuous.
>
> Bear in mind that I've only done this for the implicit functions, not 3d the
> parametrics. But I should get this sorted out and see what the problem is
> before I go any further.
>
> Thanks as always for your clear mind, sharp eyes, and _lightning fast_ code
> generation!
Hehe, no problem.
I had previously done some work related to this topic; with parametric
functions in 3D, so I already had some code to start with.
If you're interested, you can have a look at the "Trefoil Knot Tube"
example here:
https://github.com/t-o-k/scikit-vectors_examples
https://github.com/t-o-k/scikit-vectors_examples/blob/master/Trefoil_Knot_Tube.pdf
Sometimes GitHub fails to render PDF-files and Jupyter Notbook files (.ipynb).
If that happens, just wait a litte and then try again.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>
> > I ran all these through the SimpleMesh macro. See the attached image for
> > the results. I can post the complete source for that if you're interested.
>
> Yes, that would be interesting to look over.
> ...
Here's the code:
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
#version 3.7;
global_settings { assumed_gamma 1.0 }
#include "functions.inc" // For f_r()
#include "colors.inc"
#declare TAU = 2*pi;
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
#macro SimpleMesh(FnX, FnY, FnZ, MinU, MaxU, MinV, MaxV, SizeI, SizeJ)
#local LastI = SizeI - 1;
#local LastJ = SizeJ - 1;
#local Vertices = array[SizeI][SizeJ];
#local SpanU = MaxU - MinU;
#local SpanV = MaxV - MinV;
#for (I, 0, LastI)
#local U = MinU + I/LastI*SpanU;
#for (J, 0, LastJ)
#local V = MinV + J/LastJ*SpanV;
#local Vertices[I][J] =
<FnX(U, V), FnY(U, V), FnZ(U, V)>
;
#end // for
#end // for
mesh {
#for (I, 0, LastI - 1)
#for (J, 0, LastJ - 1)
#local p00 = Vertices[I ][J ];
#local p01 = Vertices[I ][J+1];
#local p10 = Vertices[I+1][J ];
#local p11 = Vertices[I+1][J+1];
triangle { p00, p10, p11 }
triangle { p11, p01, p00 }
#end // for
#end // for
}
#end // macro SimpleMesh
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
#declare FnX = function(u) { u };
#declare DFnX = function(u) { 1 };
#declare Fn_Y = array[5];
#declare DFn_Y = array[5];
#declare I = 0;
#declare Fn_Y[I] = function(u) { pow(u, 2) + 1 };
#declare DFn_Y[I] = function(u) { 2*u };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 0.4*cos(u)*(-pow(u, 2) + 3) - 1 };
#declare DFn_Y[I] = function(u) { 0.4*(pow(u, 2) - 3)*sin(u) - 0.8*u*cos(u) };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { u*u*u };
#declare DFn_Y[I] = function(u) { 3*u*u };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 4*sinh(u)/cosh(u) + 4 };
#declare DFn_Y[I] = function(u) { 16*pow(cosh(u), 2)/pow(cosh(2*u) + 1, 2) };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 8*u/(abs(u) + 1) };
#declare DFn_Y[I] = function(u) { 8/pow(abs(u) + 1, 2) };
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
#declare Nil = 1e-3;
#declare R = 0.15;
#declare Colors =
array[5] {
color Red,
color Green,
color Blue,
// color Cyan,
color Magenta,
color Yellow
}
;
#for (I, 0, 4)
#declare FnY = Fn_Y[I];
#declare DFnY = DFn_Y[I];
// Normalized component functions for tangent vector
#declare N_DFnX =
function(u) {
DFnX(u)/f_r(DFnX(u), DFnY(u), 0)
}
;
#declare N_DFnY =
function(u) {
DFnY(u)/f_r(DFnX(u), DFnY(u), 0)
}
;
object {
SimpleMesh(
function(u, v) { -R*cos(v)*N_DFnY(u) + FnX(u) }, // FnX
function(u, v) { +R*cos(v)*N_DFnX(u) + FnY(u) }, // FnY
function(u, v) { R*sin(v) }, // FnZ
-20, +20, // MinU, MaxU,
0 + Nil, TAU - Nil, // MinV, MaxV
800 + 1, 26 + 1 // SizeI, Size J
)
pigment { color Gray50 + Colors[I] }
}
#undef FnY
#undef DFnY
#undef N_DFnX
#undef N_DFnY
#end // for
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
background { color rgb <0.04, 0.02, 0.06> }
light_source {
-150*z
color White
shadowless
}
#declare AR = image_width/image_height;
camera {
orthographic
location -85*z + 0.5*y
direction z
right AR*x
up y
sky y
angle 15
}
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
(Note that the colors are more saturated than in the image I posted.)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
>
> > I ran all these through the SimpleMesh macro. See the attached image for
> > the results. I can post the complete source for that if you're interested.
>
> Yes, that would be interesting to look over.
> ...
Here's the code:
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
#version 3.7;
global_settings { assumed_gamma 1.0 }
#include "functions.inc" // For f_r()
#include "colors.inc"
#declare TAU = 2*pi;
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
#macro SimpleMesh(FnX, FnY, FnZ, MinU, MaxU, MinV, MaxV, SizeI, SizeJ)
#local LastI = SizeI - 1;
#local LastJ = SizeJ - 1;
#local Vertices = array[SizeI][SizeJ];
#local SpanU = MaxU - MinU;
#local SpanV = MaxV - MinV;
#for (I, 0, LastI)
#local U = MinU + I/LastI*SpanU;
#for (J, 0, LastJ)
#local V = MinV + J/LastJ*SpanV;
#local Vertices[I][J] =
<FnX(U, V), FnY(U, V), FnZ(U, V)>
;
#end // for
#end // for
mesh {
#for (I, 0, LastI - 1)
#for (J, 0, LastJ - 1)
#local p00 = Vertices[I ][J ];
#local p01 = Vertices[I ][J+1];
#local p10 = Vertices[I+1][J ];
#local p11 = Vertices[I+1][J+1];
triangle { p00, p10, p11 }
triangle { p11, p01, p00 }
#end // for
#end // for
}
#end // macro SimpleMesh
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
#declare FnX = function(u) { u };
#declare DFnX = function(u) { 1 };
#declare Fn_Y = array[5];
#declare DFn_Y = array[5];
#declare I = 0;
#declare Fn_Y[I] = function(u) { pow(u, 2) + 1 };
#declare DFn_Y[I] = function(u) { 2*u };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 0.4*cos(u)*(-pow(u, 2) + 3) - 1 };
#declare DFn_Y[I] = function(u) { 0.4*(pow(u, 2) - 3)*sin(u) - 0.8*u*cos(u) };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { u*u*u };
#declare DFn_Y[I] = function(u) { 3*u*u };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 4*sinh(u)/cosh(u) + 4 };
#declare DFn_Y[I] = function(u) { 16*pow(cosh(u), 2)/pow(cosh(2*u) + 1, 2) };
#declare I = I + 1;
#declare Fn_Y[I] = function(u) { 8*u/(abs(u) + 1) };
#declare DFn_Y[I] = function(u) { 8/pow(abs(u) + 1, 2) };
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
#declare Nil = 1e-3;
#declare R = 0.15;
#declare Colors =
array[5] {
color Red,
color Green,
color Blue,
// color Cyan,
color Magenta,
color Yellow
}
;
#for (I, 0, 4)
#declare FnY = Fn_Y[I];
#declare DFnY = DFn_Y[I];
// Normalized component functions for tangent vector
#declare N_DFnX =
function(u) {
DFnX(u)/f_r(DFnX(u), DFnY(u), 0)
}
;
#declare N_DFnY =
function(u) {
DFnY(u)/f_r(DFnX(u), DFnY(u), 0)
}
;
object {
SimpleMesh(
function(u, v) { -R*cos(v)*N_DFnY(u) + FnX(u) }, // FnX
function(u, v) { +R*cos(v)*N_DFnX(u) + FnY(u) }, // FnY
function(u, v) { R*sin(v) }, // FnZ
-20, +20, // MinU, MaxU,
0 + Nil, TAU - Nil, // MinV, MaxV
800 + 1, 26 + 1 // SizeI, Size J
)
pigment { color Gray50 + Colors[I] }
}
#undef FnY
#undef DFnY
#undef N_DFnX
#undef N_DFnY
#end // for
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
background { color rgb <0.04, 0.02, 0.06> }
light_source {
-150*z
color White
shadowless
}
#declare AR = image_width/image_height;
camera {
orthographic
location -85*z + 0.5*y
direction z
right AR*x
up y
sky y
angle 15
}
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
(Note that the colors are more saturated than in the image I posted.)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Droj" <803### [at] droj de> wrote:
> I was interested to see how can a 2D curve get a more interesting life in a 3D
> world.
> And I found a promising approach in the Internet on B. Frassek's website
> https://www.frassek.org (sorry, the site is in German but an automatic
> translation is available). Look for 'function graph as pipe/tube'.
> The steps are outlined here:
>
> - take the parametric function of a circle as cross section for the tube
> - determin the gradient of the 2D curve you want to use (derivatives must
> exist)
> - let the center of the cross section travel along the 2D curve (e.g. like
> insulation on a copper wire)
>
> Alas, that's it.
>
> So I started to adapt all the functions to Povray. I am aware that using atan2
> is an unexplicable mystery but what the heck.
>
> The result was sort of sobering as the tube was flatend in some parts and bulgy
> in others.
> I upload the POV-Script I generated to show the problem.
>
> Any suggestions (if there are any) on how to get a perfectly round tube are
> welcome but I need the parametric approach as I want to use the .inc/.obj output
> for more things to come.
Hi to all,
I guess this subject is rather exhausted.
Don't take me wrong I have the highest esteem for those who developed the
meshmaker macros and I am not happy to be the igorant, bloody user finding the
fly in the ointment - provided there is any as there is no proof.
Be assured the meshmaker macros work flawlessly with a heap of parametric
functions I tested.
My thanks to all who took part in this fruitful discussion and for actively
sharing their knowledge.
For the time being I will use Bill's solution to test some more curves and
produce interesting tubes including the .obj/.inc files.
And finally here's something I made in a jiffy - no great artistic work I admit. de> wrote:
> I was interested to see how can a 2D curve get a more interesting life in a 3D
> world.
> And I found a promising approach in the Internet on B. Frassek's website
> https://www.frassek.org (sorry, the site is in German but an automatic
> translation is available). Look for 'function graph as pipe/tube'.
> The steps are outlined here:
>
> - take the parametric function of a circle as cross section for the tube
> - determin the gradient of the 2D curve you want to use (derivatives must
> exist)
> - let the center of the cross section travel along the 2D curve (e.g. like
> insulation on a copper wire)
>
> Alas, that's it.
>
> So I started to adapt all the functions to Povray. I am aware that using atan2
> is an unexplicable mystery but what the heck.
>
> The result was sort of sobering as the tube was flatend in some parts and bulgy
> in others.
> I upload the POV-Script I generated to show the problem.
>
> Any suggestions (if there are any) on how to get a perfectly round tube are
> welcome but I need the parametric approach as I want to use the .inc/.obj output
> for more things to come.
Hi to all,
I guess this subject is rather exhausted.
Don't take me wrong I have the highest esteem for those who developed the
meshmaker macros and I am not happy to be the igorant, bloody user finding the
fly in the ointment - provided there is any as there is no proof.
Be assured the meshmaker macros work flawlessly with a heap of parametric
functions I tested.
My thanks to all who took part in this fruitful discussion and for actively
sharing their knowledge.
For the time being I will use Bill's solution to test some more curves and
produce interesting tubes including the .obj/.inc files.
And finally here's something I made in a jiffy - no great artistic work I admit.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Droj" <803### [at] droj de> wrote:
> "Droj" <803### [at] droj de> wrote:
> "Droj" <803### [at] droj de> wrote:
> > I was interested to see how can a 2D curve get a more interesting life in a 3D
> > world.
> > And I found a promising approach in the Internet on B. Frassek's website
> > https://www.frassek.org (sorry, the site is in German but an automatic
> > translation is available). Look for 'function graph as pipe/tube'.
> > The steps are outlined here:
> >
> > - take the parametric function of a circle as cross section for the tube
> > - determin the gradient of the 2D curve you want to use (derivatives must
> > exist)
> > - let the center of the cross section travel along the 2D curve (e.g. like
> > insulation on a copper wire)
> >
> > Alas, that's it.
> >
> > So I started to adapt all the functions to Povray. I am aware that using atan2
> > is an unexplicable mystery but what the heck.
> >
> > The result was sort of sobering as the tube was flatend in some parts and bulgy
> > in others.
> > I upload the POV-Script I generated to show the problem.
> >
> > Any suggestions (if there are any) on how to get a perfectly round tube are
> > welcome but I need the parametric approach as I want to use the .inc/.obj output
> > for more things to come.
>
> Hi to all,
>
> I guess this subject is rather exhausted.
>
> Don't take me wrong I have the highest esteem for those who developed the
> meshmaker macros and I am not happy to be the igorant, bloody user finding the
> fly in the ointment - provided there is any as there is no proof.
>
> Be assured the meshmaker macros work flawlessly with a heap of parametric
> functions I tested.
>
> My thanks to all who took part in this fruitful discussion and for actively
> sharing their knowledge.
>
> For the time being I will use Bill's solution to test some more curves and
> produce interesting tubes including the .obj/.inc files.
>
> And finally here's something I made in a jiffy - no great artistic work I admit.
Ooops, image is missing de> wrote:
> > I was interested to see how can a 2D curve get a more interesting life in a 3D
> > world.
> > And I found a promising approach in the Internet on B. Frassek's website
> > https://www.frassek.org (sorry, the site is in German but an automatic
> > translation is available). Look for 'function graph as pipe/tube'.
> > The steps are outlined here:
> >
> > - take the parametric function of a circle as cross section for the tube
> > - determin the gradient of the 2D curve you want to use (derivatives must
> > exist)
> > - let the center of the cross section travel along the 2D curve (e.g. like
> > insulation on a copper wire)
> >
> > Alas, that's it.
> >
> > So I started to adapt all the functions to Povray. I am aware that using atan2
> > is an unexplicable mystery but what the heck.
> >
> > The result was sort of sobering as the tube was flatend in some parts and bulgy
> > in others.
> > I upload the POV-Script I generated to show the problem.
> >
> > Any suggestions (if there are any) on how to get a perfectly round tube are
> > welcome but I need the parametric approach as I want to use the .inc/.obj output
> > for more things to come.
>
> Hi to all,
>
> I guess this subject is rather exhausted.
>
> Don't take me wrong I have the highest esteem for those who developed the
> meshmaker macros and I am not happy to be the igorant, bloody user finding the
> fly in the ointment - provided there is any as there is no proof.
>
> Be assured the meshmaker macros work flawlessly with a heap of parametric
> functions I tested.
>
> My thanks to all who took part in this fruitful discussion and for actively
> sharing their knowledge.
>
> For the time being I will use Bill's solution to test some more curves and
> produce interesting tubes including the .obj/.inc files.
>
> And finally here's something I made in a jiffy - no great artistic work I admit.
Ooops, image is missing
Post a reply to this message
Attachments:
Download 't_heartcurve_00b.png' (262 KB)
Preview of image 't_heartcurve_00b.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
FYI follow-up.
So I was checking out Sam Benge's code for outlining an object, and was
wondering if he could use f_th, f_ph, and f_r, and wouldn't you know it -
POV-Ray has an inbuilt function for making "tubes" from polynomials:
f_polytubes. The threshold of the isosurface functions as the thickness
parameter for the tubes.
I'd say that in future versions, the function needs to be updated, a note
provided in the documentation about the non-circularity of the "tube", or some
other improvement to the general state of affairs.
- BW
Post a reply to this message
Attachments:
Download 'polytubes.pov.txt' (2 KB)
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()