"Bald Eagle" <cre### [at] netscapenet> wrote:
> "Droj" <803### [at] drojde> wrote:
>
> Hi Oswald,
>
> I had some time to look at:
> https://www.frassek.org/3d-mathe/funktionsgraph-als-rohr-r%C3%B6hre/
>
> And I see where you're getting all of your code from, and I'm a bit disappointed
> that it isn't working "out of the box" like they seem to imply.
>
>
> While I'm happy I puzzled out some things to get the shape to look right, it's
> certainly not a general solution, which would be highly desirable.  I can
> envision using this to make text, offset curves, and generate signed distance
> functions for all manner of shapes.
>
> I would encourage you to keep working on this, and perhaps step through some
> larger values of u and render some representative frames such as are illustrated
> here:
>
>
https://image.jimcdn.com/app/cms/image/transf/dimension=301x1024:format=jpg/path/scee86bccd27a6ab2/image/idb0be97f034
4a
> 7c5/version/1573907965/konstruktion-des-funktionsgraphs-als-rohr-r%C3%B6hre.jpg
>
> Then it would be easier to see what is going wrong, and hopefully puzzle out
> why.
>
> It would be very nice indeed to be able to pass a function into a macro that
> would render a pipe/tube graph for that function.
>
> I would also keep in mind any differences in axis orientation, since it seems
> that their Y and Z axes are switched.
>
> - Bill

Hi Bill,

first of all thank you so much for encouraging me to follow up this matter and
for spending your time (may be wasting your time) to put me on the right track.

Well, I felt the same disappointment when I used the functions of B. Frassek's
page. I also tested the cardiode, the astroide and Archimeds spiral.
Same thing: flat tube in some parts!

I'm still looking for the air pump!

I spent some time to read what Wikipedia says about atan2 function.
Well, it gave me a nice headache but didn't clear the muddy waters.
The only thing I realised is that the function has to change depending on the
quadrants the graph passes.

BTW I used the macro:

#for (N, 0, tau, tau/180)
 #local X = FX (N);
 #local Y = FY (N);
 sphere {<X/4, Y/4, 0> 0.01 pigment {rgb y}}
 cylinder {0, x 0.05 pigment {rgb z} rotate z*degrees(PHI (N)) translate <X/4,
Y/4, 0>}
#end
but Povray at once complaint about 'undeclared tau'.
Can you give me a hint what that macro does? I am ignorant I know!

I promise to be persistant and as being a chemist I can be very persistant.

- Oswald

Post a reply to this message

"Droj" <803### [at] drojde> wrote:

> I spent some time to read what Wikipedia says about atan2 function.
> Well, it gave me a nice headache but didn't clear the muddy waters.
> The only thing I realised is that the function has to change depending on the
> quadrants the graph passes.

Well, I did do a lot of sleuthing last night, and got a nice diagram with the
curve, vertical circle, tangent line, angle, and rotated circle.  Seemed to work
very nicely on y=pow(x,2).

Going back to your original unedited scene, it's clear that at the very least
you have the arguments for atan2 switched - it's atan2 (y, x).  You also need to
use QY in both F1 and F2.
Im my homebrew code, I'm using atan2 (f'(x)*x, x), since that's going to be each
cathetus of the right triangle representing the tangent line and the x-axis.

That's going to require some refactoring to deal with the parametric vs implicit
 equations, but I went and did that....

.... but after that, I can't seem to straighten out the atan2 issue in your scene
code - and I'm suspecting that it may be an issue with the way that meshmaker
handles the generation of the triangles.  It may be straddling regions such that
the sides of the curve get switched, or something similar.

Hopefully I'll give it a further look and see if that's the issue.   I'm going
to try to make a much finer mesh and see if that minimizes or even eliminates
the problem.

> BTW I used the macro:
>
> #for (N, 0, tau, tau/180)
>  #local X = FX (N);
>  #local Y = FY (N);
>  sphere {<X/4, Y/4, 0> 0.01 pigment {rgb y}}
>  cylinder {0, x 0.05 pigment {rgb z} rotate z*degrees(PHI (N)) translate <X/4,
> Y/4, 0>}
> #end
> but Povray at once complaint about 'undeclared tau'.
> Can you give me a hint what that macro does? I am ignorant I know!
>
> I promise to be persistant and as being a chemist I can be very persistant.

Excellent - fellow chemist here, persistence just didn't pay off as much as it
needed to in that field.  :(

tau is simply 2*pi (available in v3.8), so you can either replace that, or just
put a line near the beginning of the scene:

#declare tau = 2*pi;

I'm confident that this is a solvable problem.

-BW

Post a reply to this message

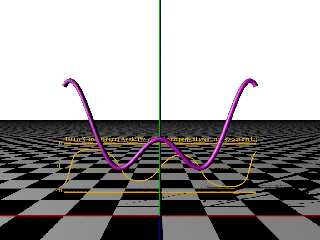
Attachments:
Download 'tubecurves.png' (117 KB)

Preview of image 'tubecurves.png'

"Bald Eagle" <cre### [at] netscapenet> wrote:

> I'm confident that this is a solvable problem.


As I said.   Success!   :)

Looks like all you have to do is change these two lines:

I got the atan to give me a "clean" curve, but it was really skinny.   "maybe
that's just rotated 90 deg from what it should be...?
So I got rid of the pi/2.  No idea _why_ that works...   yet.


#declare PHI = function (u) {-atan2( FdY(u), FdX(u) ) + pi/2*0};

#declare F1 = function(u,v) {QY(v)*sin(PHI(u)) + FX(u)};

Post a reply to this message

Attachments:
Download 'tube_heartcurve.png' (46 KB)

Preview of image 'tube_heartcurve.png'

"Bald Eagle" <cre### [at] netscapenet> wrote:
> "Bald Eagle" <cre### [at] netscapenet> wrote:
>
> > I'm confident that this is a solvable problem.
>
>
> As I said.   Success!   :)
>
> Looks like all you have to do is change these two lines:
>
> I got the atan to give me a "clean" curve, but it was really skinny.   "maybe
> that's just rotated 90 deg from what it should be...?
> So I got rid of the pi/2.  No idea _why_ that works...   yet.
>
>
> #declare PHI = function (u) {-atan2( FdY(u), FdX(u) ) + pi/2*0};
>
> #declare F1 = function(u,v) {QY(v)*sin(PHI(u)) + FX(u)};

Heureka and congratulations! You solved that 'pain in the backside'.

I adapted the POV-script according to the functions above and it looks great!
Changing QX to QY in F1 did the trick. And right, the pi/2 produces a
very, very flat curve almost like a ribbon.

I will try to do some fine tuning as the heart curve still has an inconsistency
where the dip is.

But all in all it's a beauty and I'm definitely happy.

I wish you a Merry Christmas and thank you so much.

Oswald

Post a reply to this message

"Droj" <803### [at] drojde> wrote:
> "Bald Eagle" <cre### [at] netscapenet> wrote:
> > "Bald Eagle" <cre### [at] netscapenet> wrote:
> >
> > > I'm confident that this is a solvable problem.
> >
> >
> > As I said.   Success!   :)
> >
> > Looks like all you have to do is change these two lines:
> >
> > I got the atan to give me a "clean" curve, but it was really skinny.   "maybe
> > that's just rotated 90 deg from what it should be...?
> > So I got rid of the pi/2.  No idea _why_ that works...   yet.
> >
> >
> > #declare PHI = function (u) {-atan2( FdY(u), FdX(u) ) + pi/2*0};
> >
> > #declare F1 = function(u,v) {QY(v)*sin(PHI(u)) + FX(u)};
>
> Heureka and congratulations! You solved that 'pain in the backside'.
>
> I adapted the POV-script according to the functions above and it looks great!
> Changing QX to QY in F1 did the trick. And right, the pi/2 produces a
> very, very flat curve almost like a ribbon.
>
> I will try to do some fine tuning as the heart curve still has an inconsistency
> where the dip is.
>
> But all in all it's a beauty and I'm definitely happy.
>
> I wish you a Merry Christmas and thank you so much.
>
> Oswald

PS:
Your solution works with simple Lissajous functions, too.

This is a great Christmas present!

Post a reply to this message

Attachments:
Download 't_lissa1_3_4.png' (469 KB)

Preview of image 't_lissa1_3_4.png'

"Droj" <803### [at] drojde> wrote:

> > I will try to do some fine tuning as the heart curve still has an inconsistency
> > where the dip is.

Yeah - not sure if that's the math or the macro.
It seems to be right at the beginning of the curve, so maybe instead of going
from 0 - 2pi, maybe start at pi/180 and see if that trims off the cruft.


> Your solution works with simple Lissajous functions, too.
>
> This is a great Christmas present!

I'm glad it's all working out - it definitely took a lot of staring at the code,
trying to see what each operation did and why, and even stupidly staring at
documentation I wrote myself until I finally figured out what I needed to do and
why.

https://news.povray.org/povray.binaries.images/thread/%3Cweb.606b78af565eea121f9dae3025979125%40news.povray.org%3E/

Those polynomial curves look super interesting.  It would be nice to have macros
to render all three types of curves, plus just the 2D offset curve(s).

Anyway, I'm glad you like it, and have a Merry Christmas.

- BW

Post a reply to this message

"Bald Eagle" <cre### [at] netscapenet> wrote:
> "Droj" <803### [at] drojde> wrote:
>
> > > I will try to do some fine tuning as the heart curve still has an inconsistency
> > > where the dip is.
>
> Yeah - not sure if that's the math or the macro.
> It seems to be right at the beginning of the curve, so maybe instead of going
> from 0 - 2pi, maybe start at pi/180 and see if that trims off the cruft.
>...

My suspicion is that this is caused by a problem with the Paramcalc
macro in meshmaker.inc (The SimpleMesh macro in the code below does
not seem to have this problem.)

The code below also shows an alternative way to make the final
functions for the "tube".

// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7

#version 3.7;

global_settings { assumed_gamma 1.0 }

#include "functions.inc"  // For f_r()
#include "colors.inc"

#declare TAU = 2*pi;

// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7

#macro SimpleMesh(FnX, FnY, FnZ, MinU, MaxU, MinV, MaxV, SizeI, SizeJ)

    #local SpanU = MaxU - MinU;
    #local SpanV = MaxV - MinV;
    #local LastI = SizeI - 1;
    #local LastJ = SizeJ - 1;
    #local Vertices = array[SizeI][SizeJ];
    #for (I, 0, LastI)
        // #local U = MinU + I/LastI*DU;
        #local S = I/LastI;
        #local U = MinU + S*SpanU;
        // #local U = FnU(I/LastI);
        #for (J, 0, LastJ)
            // #local V = MinV + I/LastJ*DV;
            // #local V = FnU(J/LastJ);
            #local T = J/LastJ;
            #local V = MinV + T*SpanV;
            #local Vertices[I][J] =
                <FnX(U, V), FnY(U, V), FnZ(U, V)>
            ;
        #end // for
    #end // for

    mesh {
        #for (I, 0, LastI - 1)
            #for (J, 0, LastJ - 1)
                #local p00 = Vertices[I  ][J  ];
                #local p01 = Vertices[I  ][J+1];
                #local p10 = Vertices[I+1][J  ];
                #local p11 = Vertices[I+1][J+1];
                triangle { p00, p10, p11 }
                triangle { p11, p01, p00 }
            #end // for
        #end // for
    }

#end // macro SimpleMesh

// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7

// Heart curve from https://www.frassek.org
// 0 <= u <= TAU

// Parametric functions for Heart curve and their derivatives:

#declare FnX =
    function(u) {
        16*pow(sin(u), 3)
    }
;
#declare DFnX =
    function(u) {
        48*pow(sin(u), 2)*cos(u)
    }
;

#declare FnY =
    function(u) {
        13*cos(u) - 5*cos(2*u) - 2*cos(3*u) - cos(4*u)
    }
;
#declare DFnY =
    function(u) {
        -13*sin(u) + 10*sin(2*u) + 6*sin(3*u) + 4*sin(4*u)
    }
;

// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7

#declare Nil = 1e-3;

#declare R = 1.2;


// Rotation angle of cross section of tube

#declare AngleFn =
    function(u) {
        atan2(DFnY(u), DFnX(u)) + pi/2
    }
;

union {
    SimpleMesh(
        function(u, v) { R*cos(v)*cos(AngleFn(u)) + FnX(u) },
        function(u, v) { R*cos(v)*sin(AngleFn(u)) + FnY(u) },
        function(u, v) { R*sin(v) },
        0 + Nil, TAU - Nil,
        0 + Nil, TAU - Nil,
        200, 16
    )
    sphere { <FnX(0/2*TAU), FnY(0/2*TAU), 0>, R }
    sphere { <FnX(1/2*TAU), FnY(1/2*TAU), 0>, R }
    pigment { color Gray50 + Yellow/4 }
    translate -20*x
}


// Normalized component functions for the tangent vector

#declare N_DFnX =
    function(u) {
        DFnX(u)/f_r(DFnX(u), DFnY(u), 0)
    }
;
#declare N_DFnY =
    function(u) {
        DFnY(u)/f_r(DFnX(u), DFnY(u), 0)
    }
;

union {
    SimpleMesh(
        function(u, v) { -R*cos(v)*N_DFnY(u) + FnX(u) },
        function(u, v) { +R*cos(v)*N_DFnX(u) + FnY(u) },
        function(u, v) { +R*sin(v) },
        0 + Nil, TAU - Nil,
        0 + Nil, TAU - Nil,
        200, 16
    )
    sphere { <FnX(0/2*TAU), FnY(0/2*TAU), 0>, R }
    sphere { <FnX(1/2*TAU), FnY(1/2*TAU), 0>, R }
    pigment { color Gray50 + Cyan/4 }
    translate +20*x
}

// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7

background { color rgb <0.04, 0.02, 0.06> }

light_source {
    -15*x
    color Gray50 + Red/2
    shadowless
}

light_source {
    -15*y
    color Gray50 + Green/2
    shadowless
}

light_source {
    -15*z
    color Gray50 + Blue/2
    shadowless
}

#declare AR = image_width/image_height;

camera {
   orthographic
   location -100*z
   direction z
   right AR*x
   up y
   sky y
   angle 45
}

// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7

--
Tor Olav
http://subcube.com
https://github.com/t-o-k

Post a reply to this message

"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmailcom> wrote:
> "Bald Eagle" <cre### [at] netscapenet> wrote:
> > "Droj" <803### [at] drojde> wrote:
> >
> > > > I will try to do some fine tuning as the heart curve still has an
inconsistency
> > > > where the dip is.
> >
> > Yeah - not sure if that's the math or the macro.
> > It seems to be right at the beginning of the curve, so maybe instead of going
> > from 0 - 2pi, maybe start at pi/180 and see if that trims off the cruft.
> >...
>
> My suspicion is that this is caused by a problem with the Paramcalc
> macro in meshmaker.inc (The SimpleMesh macro in the code below does
> not seem to have this problem.)
>
> The code below also shows an alternative way to make the final
> functions for the "tube".
>...

I see now that the SimpleMesh macro is a bit messy.
Here's a cleaned up version:

// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7

#macro SimpleMesh(FnX, FnY, FnZ, MinU, MaxU, MinV, MaxV, SizeI, SizeJ)

    #local LastI = SizeI - 1;
    #local LastJ = SizeJ - 1;
    #local Vertices = array[SizeI][SizeJ];
    #local SpanU = MaxU - MinU;
    #local SpanV = MaxV - MinV;
    #for (I, 0, LastI)
        #local U = MinU + I/LastI*SpanU;
        #for (J, 0, LastJ)
            #local V = MinV + J/LastJ*SpanV;
            #local Vertices[I][J] =
                <FnX(U, V), FnY(U, V), FnZ(U, V)>
            ;
        #end // for
    #end // for

    mesh {
        #for (I, 0, LastI - 1)
            #for (J, 0, LastJ - 1)
                #local p00 = Vertices[I  ][J  ];
                #local p01 = Vertices[I  ][J+1];
                #local p10 = Vertices[I+1][J  ];
                #local p11 = Vertices[I+1][J+1];
                triangle { p00, p10, p11 }
                triangle { p11, p01, p00 }
            #end // for
        #end // for
    }

#end // macro SimpleMesh

// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7

--
Tor Olav
http://subcube.com
https://github.com/t-o-k

Post a reply to this message

Le 2022-12-24 à 15:33, Droj a écrit :
> "Droj" <803### [at] drojde> wrote:
>> "Bald Eagle" <cre### [at] netscapenet> wrote:
>>> "Bald Eagle" <cre### [at] netscapenet> wrote:
>>>
>>>> I'm confident that this is a solvable problem.
>>>
>>>
>>> As I said.   Success!   :)
>>>
>>> Looks like all you have to do is change these two lines:
>>>
>>> I got the atan to give me a "clean" curve, but it was really skinny.   "maybe
>>> that's just rotated 90 deg from what it should be...?
>>> So I got rid of the pi/2.  No idea _why_ that works...   yet.
>>>
>>>
>>> #declare PHI = function (u) {-atan2( FdY(u), FdX(u) ) + pi/2*0};
>>>
>>> #declare F1 = function(u,v) {QY(v)*sin(PHI(u)) + FX(u)};
>>
>> Heureka and congratulations! You solved that 'pain in the backside'.
>>
>> I adapted the POV-script according to the functions above and it looks great!
>> Changing QX to QY in F1 did the trick. And right, the pi/2 produces a
>> very, very flat curve almost like a ribbon.
>>
>> I will try to do some fine tuning as the heart curve still has an inconsistency
>> where the dip is.
>>
>> But all in all it's a beauty and I'm definitely happy.
>>
>> I wish you a Merry Christmas and thank you so much.
>>
>> Oswald
> 
> PS:
> Your solution works with simple Lissajous functions, too.
> 
> This is a great Christmas present!
> 

Personally, for that one, I would have used a sphere_sweep using the 
bi_cubic interpolation.

Post a reply to this message

"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmailcom> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmailcom> wrote:
> > "Bald Eagle" <cre### [at] netscapenet> wrote:
> > > "Droj" <803### [at] drojde> wrote:
> > >
> > > > > I will try to do some fine tuning as the heart curve still has an
inconsistency
> > > > > where the dip is.


> > My suspicion is that this is caused by a problem with the Paramcalc
> > macro in meshmaker.inc (The SimpleMesh macro in the code below does
> > not seem to have this problem.)
> >
> > The code below also shows an alternative way to make the final
> > functions for the "tube".
> >...
>
> I see now that the SimpleMesh macro is a bit messy.

I haven't gone through any of the edited mesh macro code yet, but did some
simple mesh creation code of my own, and the problem was still in the
calculation of that damned angle Phi.  It's not very well-behaved, and jumps
around a lot, making adjacent sections of mesh "flip" through the central curve
trace.

I played around with it for quite a while, graphing the values of Phi, and
finally came up with this:

#macro Implicit_CalculatePhi (UU, I_Derivative)
 #local Phi = -atan2 (I_Derivative (UU)*UU, abs (UU+E));
 // correct for flipping around x=0
 #local Phi = select ((Phi+pi/2), Phi+pi, Phi);
 #local Phi = select (UU, -Phi, 0, Phi);

 Phi
#end

It keeps Phi as a nice, continuous value between +/-pi

So in the loops, instead of calculating Phi, just use:
#local Phi = Implicit_CalculatePhi (UU, I_Derivative);

And that seems to have eliminated all of the problems I've noticed at x0 <= 0
where there are mins and maxes in the curve.

Hopefully this does the trick.   I have more curves to plot, and then need to
adapt my macros to parametrics and then the polynomial curves.

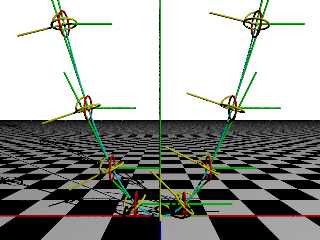
Post a reply to this message

Attachments:
Download 'tubecurves.png' (183 KB)

Preview of image 'tubecurves.png'