"Bill Pragnell" <bil### [at] hotmailcom> wrote:

> So I'm curious to know what you've done here - are you aiming for simply a
> tileable version of the crackle pattern? Can this also be colored on a per-cell
> basis like my object-based version, or is it just the tiling you're after?
>
> I'd love to see the code once it's in a fit state :)

1.  The original, long-standing, and long-desired, and often requested goal was
to have a user-defined set of cell vertices.

2.  My personal long-standing goal was to understand how to create a Voronoi
pattern from scratch.

3.  I have demonstrated that tileable Voronoi is possible, and of course, native
built-in POV-Ray tileable crackle {} is supported, but easily made even if it
wasn't.

4.  What you're currently looking at is a full, user-defined cell vertice
Voronoi pattern, that is infinitely tileable, and able to be colored on a
per-cell basis by a user-defined array.

Tdg and jr have commented that "the math" behind this is a mystery, and beyond
them.   Not so, as "the math", what little there is, is minimal, and well within
their grasp, as most of it is, or can be, handled by POV-Ray.

I was very pleased with my long-overdue understanding of how to generate a
Voronoi pattern from first principles.  You and I agreed that the scalar output
of the function would "scrub" any information about the underlying cells, which
it does.

But as I was working the tiled version, the truth of the matter finally made
it's way through to me, and the solution is what I am calling POV-Ray CHEMistry.

The Coding-Human-Elementary Math interplay.

The Voronoi pattern is a "semiprocedural" pattern generated int he following
way:
You define the cell vertex points. [A, B, C, ....]
You calculate the distance between the current pixel (P) and each vertex point.
This amounts to vlength (A-P)
Then you just use a #for loop to shove all the distance calculations into a min
() statement to find the shortest distance / closest point.
You can use a select () function to limit the "reach" of this if you want...


So the output of the Voronoi function is a scalar distance.
It has no memory of where this number came from, and the math does not give us
any additional information.

But we are not limited to math, are we?
We are humans, and capable of recognizing patterns and properties, and reasoning
outside of the math.

And this is where are able to write the code to get the coordinates of the cell
vertex that generated the distance.

Pick any point in any of the Voronoi cells, and what do we know about it?
We know that that point is closer to that cell's vertex than any other cell
vertex - because this is the definition of the pattern.  So if I now (again)
calculate the distance between that pixel and every cell vertex, it will only
match a single Voronoi result in the original function.
How do we apply this Human understanding to the math and the code?
We compare the distance between the current pixel and each cell vertex to see if
they are equal.
This easily done by subtracting one from the other, since if they are equal,
then the result is zero.
So we can plug this into a select () statement, and if Distance-Voronoi is zero,
then --- return the Spline Index value for that vertex, otherwise, zero.

But we need to do this for ALL of the cell vertices, and so all we do is once
again use a #for loop to shove all those calculations into a sum () function.
All of the vertices that _aren't_ the closest one sum to zero, but the closest
one adds its Spline Index value to the result.

Now, we can define a parallel spline function that indexes RGB color values
instead of cell vertices.

And, instead of coloring the pixel based upon the grayscale value of the
distance function, we can just use the RGB value that the user assigns to that
cell vertex to color _every_ pixel that is closest to that cell vertex.

And there you go - full color, solid Voronoi, from SDL-only scalar-only POV-Ray
functions.

We can then use the distance function to multiply the rgb value to get colored
shading, and the index value to define other arrays for textures, finishes,
normals, etc.

To make this tile infinitely, we just restrict the vertices to the 0-1 range,
and use select () and abs () to make mod() behave nicely across the -, 0, +
transition.

I'll hopefully clean up some of the code this weekend, and add a full discussion
of this as a section to my Function Monograph that I started writing for folks
like Kenneth.

I'll have to take a look at why it's SO SLOW.   But other than that, I'd say
that future development would include a weighted Voronoi (which may be analogous
to POV-Ray's crackle form vector), a 3D version / expansion of the current
implementation, and also figuring out the best way to implement the Delaunay
triangulation - either from first principles, or by using the Voronoi as a
basis.
I'm thinking that a 3-pass Voronoi pattern would give the 3 closest cell
vertices, and then I can use triangle {} to show the pattern.


Also, maybe we can apply this POV-Ray CHEMistry to some past problems or new
projects to see how far we can push it.

Post a reply to this message

Attachments:
Download 'tileablevoronoitest.png' (96 KB)

Preview of image 'tileablevoronoitest.png'

kurtz le pirate <kur### [at] gmailcom> wrote:

> This kind of code is a very big mystery to me :(
> T-O-K also uses it a lot in his code about complex functions.

It doesn't need to be, and once you understand the basics of how it works, it's
a very powerful technique that you can use a wide variety of purposes.

You can get a simple idea of how it all works by defining a simple distance
function to any pixel.   vlength (x, y, z) is the Euclidian distance to any
pixel from the origin.

So just do:

#declare Distance = function {vlength (x, y, z)}
and then do

plane {z, 0 pigment {function {Distance (x, y, z}}



> It's strange from you ...
> Is your code recursif ?

It's not - it's a few simple functions that are just layered together.  I just
wrote a description of how it all works.

Post a reply to this message

On 02/12/2022 21:48, Bald Eagle wrote:
> kurtz le pirate <kur### [at] gmailcom> wrote:
> 
>> This kind of code is a very big mystery to me :(
>> T-O-K also uses it a lot in his code about complex functions.
> 
> It doesn't need to be, and once you understand the basics of how it works, it's
> a very powerful technique that you can use a wide variety of purposes.
> 
> You can get a simple idea of how it all works by defining a simple distance
> function to any pixel.   vlength (x, y, z) is the Euclidian distance to any
> pixel from the origin.
> 
> So just do:
> 
> #declare Distance = function {vlength (x, y, z)}
> and then do
> 
> plane {z, 0 pigment {function {Distance (x, y, z}}
> 

LOL !
2.2.1.6 User-Defined Functions
...Excluded are for example strlen or vlength...



and thank you for this little example that sheds a little
light on my lantern




-- 
Kurtz le pirate
Compagnie de la Banquise

Post a reply to this message

kurtz le pirate <kur### [at] gmailcom> wrote:

> LOL !
> 2.2.1.6 User-Defined Functions
> ...Excluded are for example strlen or vlength...

Ugh.   I hate that.
// Length or Norm
#declare Vlength = function (ax, ay, az) {sqrt(ax*ax + ay*ay + az*az)}

Take that, POV-Ray, function parser!

The other thing I have learned from sifting through ShaderToy code is that
vdot (v, v) gives the square of the length of vector v.
so maybe just use that, or try sqrt(vdot(<x, y, z>, <x, y, z>)), if the parser
doesn't choke on that.
My brain has not fully "locked on" to what functions allow and what needs a
silly workaround.

And now that I'm looking for the input syntax specifics (there are none), I see:
(under math.inc) (a workaround file)

vdot(V1,V2)
Dot product of V1 and V2. Returns a float value that is the dot product
(sometimes called scalar product) of V1 with V2. It is directly proportional to
the length of the two vectors and the cosine of the angle between them. Formula
is vdot=V1.x*V2.x + V1.y*V2.y + V1.z*V2.z. See the animated demo scene VECT2.POV
for an illustration.

vlength(V)
Length of V. Returns a float value that is the length of vector V. Formula is
vlength=sqrt(vdot(A,A)). Can be used to compute the distance between two points.
Dist=vlength(V2-V1)



But just try function {x}, or y , or z.
square them
sqrt
abs()
mod (x, 1)

and then once you've discovered the sheer delight of this method, you can add
the wonderful select () into the mix.

Post a reply to this message

On 03/12/2022 16:07, Bald Eagle wrote:
> kurtz le pirate <kur### [at] gmailcom> wrote:
> 
>> LOL !
>> 2.2.1.6 User-Defined Functions
>> ...Excluded are for example strlen or vlength...
> 
> Ugh.   I hate that.
> // Length or Norm
> #declare Vlength = function (ax, ay, az) {sqrt(ax*ax + ay*ay + az*az)}
> 
> Take that, POV-Ray, function parser!
> 

Don't worry about the Vlength, I had corrected it myself.
But it's funny that your example falls on an unauthorized function.


I'm moving slowly but I think I've seen too much complication all at
once. I made this :

plane {
 y, 0
 pigment {
  function {
   hsl2rgb ( << selected line for the error
    fnHue(x,z),
    Saturation,
    fnLightness(x,z)
    )
   }
  }
 }

and i get this error : Float expected but vector or color expression found.

I made this (very very simplified complex representation) :
#declare fnHue = function(re,im) { mod(degrees(atan2(im,re)),360) }
#declare fnLightness = function(re,im) { sqrt(re*re+im*im) }
#declare Saturation = 1.0;


'hsl2rgb' is a small macro that converts HSL to RGB from
<https://www.rapidtables.com/convert/color/hsl-to-rgb.html>

#macro hsl2rgb (H,S,L)
 #local C=(1-abs(2*L-1))*S;
 #local X=C*(1-abs(mod(H/60,2)-1));
 #local m=L-(C/2);
 #local l = 0.99999999;
 #switch (H)
  #range (0,60*l)
   #local r=<C,X,0>;
  #break
  #range (60,120*l)
   #local r=<X,C,0>;
  #break
  #range (120,180*l)
   #local r=<0,C,X>;
  #break
  #range (180,240*l)
   #local r=<0,X,C>;
  #break
  #range (240,300*l)
   #local r=<X,0,C>;
  #break
  #range (300,360*l)
   #local r=<C,0,X>;
  #break
 #end
 r*m
#end


Why this "Float expected but vector or color expression" ?
I still have a lot to learn ...




-- 
Kurtz le pirate
Compagnie de la Banquise

Post a reply to this message

kurtz le pirate <kur### [at] gmailcom> wrote:

> and i get this error : Float expected but vector or color expression found.

> Why this "Float expected but vector or color expression" ?
> I still have a lot to learn ...

What you are experiencing is the lack of crossover between the POV-Ray SDL
parser and the function parser.

When you are using x, y, z in SDL, those refer to the basis vectors of the
cardinal axes.

When those variables are evaluated in a function, they refer to the scalar
components of the pixel coordinates being evaluated.

So the function is expecting x to be a scalar value, but you are feeding it <1,
0, 0>.

Post a reply to this message

I made the type of function you're looking for, but I can't find the link to it,
assuming I posted it.

But Trevor Quayle wrote one also:

http://news.povray.org/povray.general/message/%3Cweb.4784496ba8d0eaa2ae8612c0%40news.povray.org%3E/#%3Cweb.4784496ba8d0
eaa2ae8612c0%40news.povray.org%3E

See how it's written differently than a macro.

Once you define a function, that's it.  You're done.
When POV-Ray evaluates things during render time, anything in the code has
already executed and finished.  That's why you can't stick macros into functions
for render time, use macros during render time, or change what a function
evaluates to  (the underlying equation) during render time.

Functions are equations.   Macros are algorithms.  It helps to think about it
that way to understand the difference and stay out of trouble.

Post a reply to this message

Thomas de Groot <tho### [at] degrootorg> wrote:

> Would it be possible to vary the /size/ of the individual cells? in a
> random way?

I managed to get a tilable pattern with _more_ randomness, not sure this is
exactly what you or I was imagining.

Got some weird artifacts / cutoff / transitions when I tried to push the
envelope, so I may have to start a little fresher to get this thing to work
right.

Post a reply to this message

Attachments:
Download 'nongridtileablevoronoi.png' (171 KB)

Preview of image 'nongridtileablevoronoi.png'

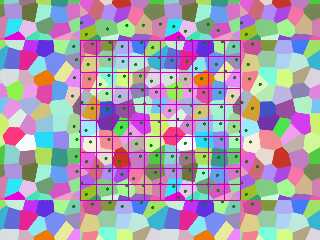
"Bald Eagle" <cre### [at] netscapenet> wrote:

> 4.  What you're currently looking at is a full, user-defined cell vertice
> Voronoi pattern, that is infinitely tileable, and able to be colored on a
> per-cell basis by a user-defined array.

Well.  Almost.

I have to figure out why the cells are getting colored differently across the
hard transition of the unit square.  The pattern is tiling, but the color -
isn't.

I haven't had a few clear, focused hours to pick at all the parts and invent
debugging tools to see what's happening and why.  But it's very very close.

And still very very slow.   :(

Post a reply to this message

Attachments:
Download 'tileablevoronoitest.png' (146 KB)

Preview of image 'tileablevoronoitest.png'

Il 26/11/2022 00:20, Bill Pragnell ha scritto:

This is lovely!

Paolo

Post a reply to this message