 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Hi
Since this post:
From: kurtz le pirate
Subject: How to ...
Date: 2021-11-22 11:23:08
http://news.povray.org/povray.general/thread/%3C619bc3ec%241%40news.povray.org%3E/
- I've been working on some some macros that create functions for calculating
with complex numbers.
And yesterday I made some functions that can be used for HSV-coloring of
pigments.
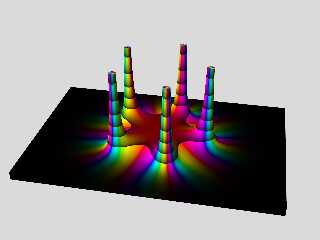
The isosurface in the attached image shows the magnitude (or modulus) of this
function:
Fn(Z) = 1/(Z^5 - 2)^2
- as the height above a complex plane:. I found that function here:
https://matlabarticlesworld.blogspot.com/2020/01/what-is-coolest-thing-you-can-do-with.html
The colors are chosen so that the hue follows the phase (or argument) of the
function, while the lightness goes from 0.0 to 0.5 in intervals along the height
axis. The saturation is 100% everywhere.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
Attachments:
Download 'isosurface from magnitude of complex function.png' (344 KB)
Preview of image 'isosurface from magnitude of complex function.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> Hi
>
> Since this post:
>
> From: kurtz le pirate
> Subject: How to ...
> Date: 2021-11-22 11:23:08
> http://news.povray.org/povray.general/thread/%3C619bc3ec%241%40news.povray.org%3E/
>
> - I've been working on some some macros that create functions for calculating
> with complex numbers.
>
> And yesterday I made some functions that can be used for HSV-coloring of
> pigments.
>
> The isosurface in the attached image shows the magnitude (or modulus) of this
> function:
>
> Fn(Z) = 1/(Z^5 - 2)^2
>
> - as the height above a complex plane:. I found that function here:
>
https://matlabarticlesworld.blogspot.com/2020/01/what-is-coolest-thing-you-can-do-with.html
>
> The colors are chosen so that the hue follows the phase (or argument) of the
> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> axis. The saturation is 100% everywhere.
>
> --
> Tor Olav
> http://subcube.com
> https://github.com/t-o-k
I hope you won't mind that I love it... without understanding it :-) com> wrote:
> Hi
>
> Since this post:
>
> From: kurtz le pirate
> Subject: How to ...
> Date: 2021-11-22 11:23:08
> http://news.povray.org/povray.general/thread/%3C619bc3ec%241%40news.povray.org%3E/
>
> - I've been working on some some macros that create functions for calculating
> with complex numbers.
>
> And yesterday I made some functions that can be used for HSV-coloring of
> pigments.
>
> The isosurface in the attached image shows the magnitude (or modulus) of this
> function:
>
> Fn(Z) = 1/(Z^5 - 2)^2
>
> - as the height above a complex plane:. I found that function here:
>
https://matlabarticlesworld.blogspot.com/2020/01/what-is-coolest-thing-you-can-do-with.html
>
> The colors are chosen so that the hue follows the phase (or argument) of the
> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> axis. The saturation is 100% everywhere.
>
> --
> Tor Olav
> http://subcube.com
> https://github.com/t-o-k
I hope you won't mind that I love it... without understanding it :-)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Mr" <nomail@nomail> wrote:
>...
> I hope you won't mind that I love it... without understanding it :-)
I don't mind at all =))
Learning the basics of imaginary and complex numbers is not very hard. It's
about learning new ways of adding, subtracting, multiplying, dividing etc. It's
understanding how they can be used and how to interpret the results that can be
challenging.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> Hi
>
> Since this post:
>
> From: kurtz le pirate
> Subject: How to ...
> Date: 2021-11-22 11:23:08
> http://news.povray.org/povray.general/thread/%3C619bc3ec%241%40news.povray.org%3E/
>
> - I've been working on some some macros that create functions for calculating
> with complex numbers.
>
> And yesterday I made some functions that can be used for HSV-coloring of
> pigments.
>
> The isosurface in the attached image shows the magnitude (or modulus) of this
> function:
>
> Fn(Z) = 1/(Z^5 - 2)^2
>
> - as the height above a complex plane:. I found that function here:
>
https://matlabarticlesworld.blogspot.com/2020/01/what-is-coolest-thing-you-can-do-with.html
>
> The colors are chosen so that the hue follows the phase (or argument) of the
> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> axis. The saturation is 100% everywhere.
>
> --
> Tor Olav
> http://subcube.com
> https://github.com/t-o-k
Very nice.
The "multi-layered" aspect of the result is intriguing me. Does it come from a
property of the function you've choosen, or from the way you choose to visualise
it ?
Pascal com> wrote:
> Hi
>
> Since this post:
>
> From: kurtz le pirate
> Subject: How to ...
> Date: 2021-11-22 11:23:08
> http://news.povray.org/povray.general/thread/%3C619bc3ec%241%40news.povray.org%3E/
>
> - I've been working on some some macros that create functions for calculating
> with complex numbers.
>
> And yesterday I made some functions that can be used for HSV-coloring of
> pigments.
>
> The isosurface in the attached image shows the magnitude (or modulus) of this
> function:
>
> Fn(Z) = 1/(Z^5 - 2)^2
>
> - as the height above a complex plane:. I found that function here:
>
https://matlabarticlesworld.blogspot.com/2020/01/what-is-coolest-thing-you-can-do-with.html
>
> The colors are chosen so that the hue follows the phase (or argument) of the
> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> axis. The saturation is 100% everywhere.
>
> --
> Tor Olav
> http://subcube.com
> https://github.com/t-o-k
Very nice.
The "multi-layered" aspect of the result is intriguing me. Does it come from a
property of the function you've choosen, or from the way you choose to visualise
it ?
Pascal
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: Thomas de Groot
Subject: Re: Isosurface from magnitude of complex function with domain coloring
Date: 23 Dec 2021 02:32:24
Message: <61c42608$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
Somehow, this makes me think of black hole gravity wells...
Intriguing!
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: Alain Martel
Subject: Re: Isosurface from magnitude of complex function with domain coloring
Date: 24 Dec 2021 13:16:26
Message: <61c60e7a$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
Le 2021-12-22 à 19:34, BayashiPascal a écrit :
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>> Hi
>>
>> Since this post:
>>
>> From: kurtz le pirate
>> Subject: How to ...
>> Date: 2021-11-22 11:23:08
>> http://news.povray.org/povray.general/thread/%3C619bc3ec%241%40news.povray.org%3E/
>>
>> - I've been working on some some macros that create functions for calculating
>> with complex numbers.
>>
>> And yesterday I made some functions that can be used for HSV-coloring of
>> pigments.
>>
>> The isosurface in the attached image shows the magnitude (or modulus) of this
>> function:
>>
>> Fn(Z) = 1/(Z^5 - 2)^2
>>
>> - as the height above a complex plane:. I found that function here:
>>
https://matlabarticlesworld.blogspot.com/2020/01/what-is-coolest-thing-you-can-do-with.html
>>
>> The colors are chosen so that the hue follows the phase (or argument) of the
>> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
>> axis. The saturation is 100% everywhere.
>>
>> --
>> Tor Olav
>> http://subcube.com
>> https://github.com/t-o-k
>
>
> Very nice.
>
> The "multi-layered" aspect of the result is intriguing me. Does it come from a
> property of the function you've choosen, or from the way you choose to visualise
> it ?
>
> Pascal
>
>
>
Do you mean the repeating gradient ?
It comes from the way the «V» of the HSV value is computed, and values
larger than 1 get their integer part zeroed.
Then, it's mapped to a 0..0.5 range.
It could look something like this :
colour_map{
[0 hsv2rgb(<Hvalue, 1, 0>)]
[1 hsv2rgb(<Hvalue, 1, 0.5>)]
} com> wrote:
>> Hi
>>
>> Since this post:
>>
>> From: kurtz le pirate
>> Subject: How to ...
>> Date: 2021-11-22 11:23:08
>> http://news.povray.org/povray.general/thread/%3C619bc3ec%241%40news.povray.org%3E/
>>
>> - I've been working on some some macros that create functions for calculating
>> with complex numbers.
>>
>> And yesterday I made some functions that can be used for HSV-coloring of
>> pigments.
>>
>> The isosurface in the attached image shows the magnitude (or modulus) of this
>> function:
>>
>> Fn(Z) = 1/(Z^5 - 2)^2
>>
>> - as the height above a complex plane:. I found that function here:
>>
https://matlabarticlesworld.blogspot.com/2020/01/what-is-coolest-thing-you-can-do-with.html
>>
>> The colors are chosen so that the hue follows the phase (or argument) of the
>> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
>> axis. The saturation is 100% everywhere.
>>
>> --
>> Tor Olav
>> http://subcube.com
>> https://github.com/t-o-k
>
>
> Very nice.
>
> The "multi-layered" aspect of the result is intriguing me. Does it come from a
> property of the function you've choosen, or from the way you choose to visualise
> it ?
>
> Pascal
>
>
>
Do you mean the repeating gradient ?
It comes from the way the «V» of the HSV value is computed, and values
larger than 1 get their integer part zeroed.
Then, it's mapped to a 0..0.5 range.
It could look something like this :
colour_map{
[0 hsv2rgb(<Hvalue, 1, 0>)]
[1 hsv2rgb(<Hvalue, 1, 0.5>)]
}
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>
> The colors are chosen so that the hue follows the phase (or argument) of the
> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> axis. The saturation is 100% everywhere.
>
Those beautiful color gradations remind me of old-style blown-glass/metallic
Christmas tree ornaments; it even appears as if they have blurred reflections.
That's an amazing result. Nice! com> wrote:
>
> The colors are chosen so that the hue follows the phase (or argument) of the
> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> axis. The saturation is 100% everywhere.
>
Those beautiful color gradations remind me of old-style blown-glass/metallic
Christmas tree ornaments; it even appears as if they have blurred reflections.
That's an amazing result. Nice!
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> - I've been working on some some macros that create functions for calculating
> with complex numbers.
Very nice.
I was consulting the stuff that Paul Nylander wrote. I'm assuming yours are
similar.
(He's using loops and macros to make triangles...)
//Complex Functions
#macro Square(X) X*X #end
#macro Complex(X,Y) <X,Y> #end
#declare I=Complex(0,1);
#macro Re(Z) Z.x #end
#macro Im(Z) Z.y #end
#macro Abs(Z) vlength(Z) #end // sqrt(square(Re(Z))+square(Im(Z)))
#macro Arg(Z)
#if(Abs(Z)=0)
#local theta=0;
#else
#local theta=atan2(Im(Z),Re(Z));
#end
theta
#end
#macro Sqr(Z) Complex(square(Re(Z))-square(Im(Z)),2*Re(Z)*Im(Z)) #end
#macro Pow(Z,n)
#local r=Abs(Z);
#if(r=0)
#local z2=Complex(0,0);
#else
#local theta=n*Arg(Z);
#local z2=pow(r,n)*Complex(cos(theta),sin(theta));
#end
z2
#end
#macro Mult(z1,z2)
Complex(Re(z1)*Re(z2)-Im(z1)*Im(z2),Im(z1)*Re(z2)+Re(z1)*Im(z2)) #end
#macro Exp(Z) exp(Re(Z))*Complex(cos(Im(Z)),sin(Im(Z))) #end
#macro Sinh(Z) Complex(cos(Im(Z))*sinh(Re(Z)),sin(Im(Z))*cosh(Re(Z))) #end
#macro Cosh(Z) Complex(cos(Im(Z))*cosh(Re(Z)),sin(Im(Z))*sinh(Re(Z))) #end
I made these two to just keep track
#macro Argument (Re, Im)
atan2 (Re, Im)
#end
#macro Modulus (Re, Im)
sqrt (pow (Re, 2) + pow (Im, 2))
#end
> And yesterday I made some functions that can be used for HSV-coloring of
> pigments.
I worked those out from the macros in colors.inc. A little challenging at first
to turn that whole thing into a function. ;)
This is looking great! I'm sure there are a lot of other interesting complex
surfaces to be explored. I'm also wondering how hard it would be to use mod()
to have an infinite array of those "black hole vortices" on a plane - in either
a rectangular or an alternating/hexagonal arrangement... com> wrote:
> - I've been working on some some macros that create functions for calculating
> with complex numbers.
Very nice.
I was consulting the stuff that Paul Nylander wrote. I'm assuming yours are
similar.
(He's using loops and macros to make triangles...)
//Complex Functions
#macro Square(X) X*X #end
#macro Complex(X,Y) <X,Y> #end
#declare I=Complex(0,1);
#macro Re(Z) Z.x #end
#macro Im(Z) Z.y #end
#macro Abs(Z) vlength(Z) #end // sqrt(square(Re(Z))+square(Im(Z)))
#macro Arg(Z)
#if(Abs(Z)=0)
#local theta=0;
#else
#local theta=atan2(Im(Z),Re(Z));
#end
theta
#end
#macro Sqr(Z) Complex(square(Re(Z))-square(Im(Z)),2*Re(Z)*Im(Z)) #end
#macro Pow(Z,n)
#local r=Abs(Z);
#if(r=0)
#local z2=Complex(0,0);
#else
#local theta=n*Arg(Z);
#local z2=pow(r,n)*Complex(cos(theta),sin(theta));
#end
z2
#end
#macro Mult(z1,z2)
Complex(Re(z1)*Re(z2)-Im(z1)*Im(z2),Im(z1)*Re(z2)+Re(z1)*Im(z2)) #end
#macro Exp(Z) exp(Re(Z))*Complex(cos(Im(Z)),sin(Im(Z))) #end
#macro Sinh(Z) Complex(cos(Im(Z))*sinh(Re(Z)),sin(Im(Z))*cosh(Re(Z))) #end
#macro Cosh(Z) Complex(cos(Im(Z))*cosh(Re(Z)),sin(Im(Z))*sinh(Re(Z))) #end
I made these two to just keep track
#macro Argument (Re, Im)
atan2 (Re, Im)
#end
#macro Modulus (Re, Im)
sqrt (pow (Re, 2) + pow (Im, 2))
#end
> And yesterday I made some functions that can be used for HSV-coloring of
> pigments.
I worked those out from the macros in colors.inc. A little challenging at first
to turn that whole thing into a function. ;)
This is looking great! I'm sure there are a lot of other interesting complex
surfaces to be explored. I'm also wondering how hard it would be to use mod()
to have an infinite array of those "black hole vortices" on a plane - in either
a rectangular or an alternating/hexagonal arrangement...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Alain Martel <kua### [at] videotron ca> wrote:
> Do you mean the repeating gradient ?
> larger than 1 get their integer part zeroed.
>
> Then, it's mapped to a 0..0.5 range.
>
> It could look something like this :
> colour_map{
> [0 hsv2rgb(<Hvalue, 1, 0>)]
> [1 hsv2rgb(<Hvalue, 1, 0.5>)]
> }
I mean, looking at the bottom-left corner, or the concentric pattern in the cut
at the top of the singularities, I see it as a superposition of several
surfaces. Also, the shape of the singularities seems to have slight steps, at
the border of what I believe to be each layer. But the more I look at it the
more I feel like I'm just completely confused by the repeating colour pattern
and the shape of the isosurface... which makes this image even more intriguing
:-)
Pascal ca> wrote:
> Do you mean the repeating gradient ?
> larger than 1 get their integer part zeroed.
>
> Then, it's mapped to a 0..0.5 range.
>
> It could look something like this :
> colour_map{
> [0 hsv2rgb(<Hvalue, 1, 0>)]
> [1 hsv2rgb(<Hvalue, 1, 0.5>)]
> }
I mean, looking at the bottom-left corner, or the concentric pattern in the cut
at the top of the singularities, I see it as a superposition of several
surfaces. Also, the shape of the singularities seems to have slight steps, at
the border of what I believe to be each layer. But the more I look at it the
more I feel like I'm just completely confused by the repeating colour pattern
and the shape of the isosurface... which makes this image even more intriguing
:-)
Pascal
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: kurtz le pirate
Subject: Re: Isosurface from magnitude of complex function with domain coloring
Date: 25 Dec 2021 04:56:55
Message: <61c6eae7@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 22/12/2021 06:51, Tor Olav Kristensen wrote:
> Hi
>
> Since this post:
>
> From: kurtz le pirate
> Subject: How to ...
> Date: 2021-11-22 11:23:08
> http://news.povray.org/povray.general/thread/%3C619bc3ec%241%40news.povray.org%3E/
>
> - I've been working on some some macros that create functions for calculating
> with complex numbers.
>
> And yesterday I made some functions that can be used for HSV-coloring of
> pigments.
>
> The isosurface in the attached image shows the magnitude (or modulus) of this
> function:
>
> Fn(Z) = 1/(Z^5 - 2)^2
>
> - as the height above a complex plane:. I found that function here:
>
https://matlabarticlesworld.blogspot.com/2020/01/what-is-coolest-thing-you-can-do-with.html
>
> The colors are chosen so that the hue follows the phase (or argument) of the
> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> axis. The saturation is 100% everywhere.
Very good job !
The basic operators on the complexes is much more elaborate than mine. I
use simple macros. This makes the definitions a little more difficult to
work out. For example, for f(z) = z + 1/z, I have to write
complexAdd(cc,complexInverse(cc)).
The really interesting part is the use of isosurfaces. Good job. I just
used colored triangles which give me a {} mesh. The coloring model is
also very clever because the hue and luminosity depend on the value of
the function.
I will see how to add the same coloring scheme as you.
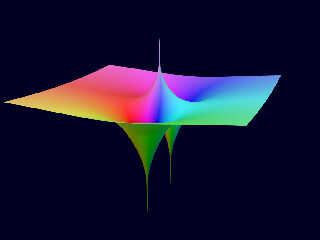
Here, one sample of f(z) = (-z^3 + iz^2 + 1) / (z - 1 + i)^2.
--
Kurtz le pirate
Compagnie de la Banquise
Post a reply to this message
Attachments:
Download 'complex3dmesh_02_fn2.jpg' (48 KB)
Preview of image 'complex3dmesh_02_fn2.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()