 |
|
|
|
|
|
| |
| |
|
|
|
|
| |
| |
|
|
"Bald Eagle" <cre### [at] netscape net> wrote:
> This was very exciting to me, as it solves some problems I've had with sine
> waves and offset curves.
> But as you can see, it also fixes the scaling of the thickness of an ellipse.
> You can imagine this being used to fix a torus scaled into an elliptical torus.
AND .... this same approach was implemented by ... user And in 2013 to make
constant-thickness isosurface shells.
http://news.povray.org/povray.binaries.images/thread/%3Cweb.5264d1b954cff585cc1fd1150%40news.povray.org%3E/?ttop=423056
&toff=750&mtop=423452&moff=10
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Whereupon Tor Olav Kristensen made a whopping follow-up post:
http://news.povray.org/povray.binaries.images/message/%3Cweb.5b5e768edce0719a79917fa00%40news.povray.org%3E/#%3Cweb.5b5
e768edce0719a79917fa00%40news.povray.org%3E
Especially interesting, with regard to the f_r function and fn_Gradient macro.
That ties in to the calculation of normals and using the object pattern in an
isosurface.
I suppose I'll also do a little light reading about the Laplacian operator and
the elliptic operator, since they are directly related. ;)
With regard to the elliptical torus, I'm not exactly sure what throws off the 3D
shape. With the standard circular torus, we just use R minus the length of the
x,z vector to get one side of the right triangle to evaluate the minor radius'
circle, and y becomes the other.
Generalizing this to an ellipse really seems like it should work without issue,
but obviously it doesn't.
It seems that any circle "drawn" ought to be in the plane bisecting the angle
formed by the two foci and the point on the ellipse.
It also seems like there's trend where the torus extends outward too much in the
direction of the longest semi-axis, and not enough in the shortest semi-axis.
Which leads me to intuitively believe that there ought to be a way to use a and
b to compensate for how the torus gets thrown off.
And that's all I have for now.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 5/15/20 2:09 PM, Bald Eagle wrote:
> Whereupon Tor Olav Kristensen made a whopping follow-up post:
>
...
>
> And that's all I have for now.
>
Unsure how helpful, but I'd read in the past supertoroids a good way to
create various csg modeling shapes.
Along with other work brought up a parametric supertoroid alongside a
parametric of Cousin Ricky's include macro. The latter is a subset of
the former's function! See the attached image(2).
Good news, right... We can find, half a dozen, slightly different,
supposed, implicit equations in books, papers and the web for
supertoroids. Another day plus of struggle and I've not a single attempt
that does the a, b scaling correctly - most equations have other issues
too(3). I'm struggling with gradients in all of the implicit forms,
which makes trying ideas slow(4).
Aside:
----
I made an attempt too using my updated f_ellipsoid function creating
first an x,y shell with the proper scaling. Used my new f_multiply1to8
to get something torus like as well as some other forms.
The issue - perhaps like that you were up against in one of your posts -
is, while the surface (the roots) with respect to x,y are in the
correct(1) places, the gradients 'inside' are not of uniform value
around the ring. To a first order the multiplication affects z around
the ring, but I suspect the gradients are also not symmetrical about the
central supertorus axis. Not been able to come up with the right
corrections for even the first order z issue - yet again. :-)
If you or I get this going, Ricky's invoice is going to huge! :-)
Bill P.
(1) - Getting a supertoroid implicit which matches in every respect the
parametric one a worthy goal no matter, but I worry some whether the
resulting super torus will always be the right shape. I think it likely
depends on the approach taken with the rest of the 'csg' - and perhaps
some of the forms you've come up with might be what's needed.
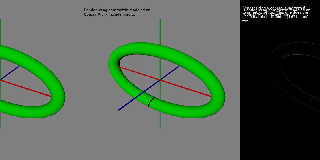
(2) - Differences shown at a 2x multiple. These are due using compute
depths of 8 and 18 with other accuracy items the same. Not too
surprising, but interesting to see.
(3) - The function's terms and how they play with C++/SDL ones given
different e1/e2 parameters is tricky (abs() is your friend). Yep,
possible one or more forms is correctly as presented and it's me not
getting something right.
(4) - Isosurfaces, when not just slow, suddenly blinking out of
existence all or in part. It's as much the problem as slow renders and
forces high gradient settings 500, 1000 or to avoid.
Post a reply to this message
Attachments:
Download 'supertor_chapter7.jpg' (51 KB)
Preview of image 'supertor_chapter7.jpg'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
I just stumbled across this while trying to regain my sanity,
and if even Ramanujan couldn't come up with anything but an approximation, than
I think the rest of us are Fuuuuuuuuuuuuuuuuuuuuuumbling around in the dark.
:)
https://www.youtube.com/watch?v=5nW3nJhBHL0
But don't anyone think that that will stop us from making another attempt, using
new inspiration and mathematical tools!
I think the above implies that due to the interesting properties of ellipses,
that a workable solution will use numerical methods.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 2020-09-20 6:24 PM (-4), Bald Eagle wrote:
> I just stumbled across this while trying to regain my sanity,
> and if even Ramanujan couldn't come up with anything but an approximation, than
> I think the rest of us are Fuuuuuuuuuuuuuuuuuuuuuumbling around in the dark.
>
> :)
>
> https://www.youtube.com/watch?v=5nW3nJhBHL0
You watch Matt Parker to regain your sanity? I have some of his videos
languishing in my "Watch later" list because I'm afraid I'll *lose* my
sanity if I watch them.
> But don't anyone think that that will stop us from making another attempt, using
> new inspiration and mathematical tools!
>
> I think the above implies that due to the interesting properties of ellipses,
> that a workable solution will use numerical methods.
I am not convinced that this property is directly relevant to the
problem I am trying to solve. I still think the key is in that quartic
equation I came up with, which should not require numerical methods
(beyond what's implicit in POV-Ray's built-in functions). The problem
is that I am not practiced in solving quartic equations.
P.S. I have known since 2007 that there is no exact formula for an
ellipse's circumference. I discovered that while trying to weld this
'O' to the rectangular plate using an ellipse made out of blobs.
Post a reply to this message
Attachments:
Download 'povanized-b.png' (100 KB)
Preview of image 'povanized-b.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Cousin Ricky <ric### [at] yahoocom> wrote:
> You watch Matt Parker to regain your sanity?
After spending most of the weekend trying to work out partial differential
equations of 2D Bernstein polynomials, and Gaussian curvature?
Sure.
After that, lifting boxes at work on Monday was relaxing :D
Watching Daniel Shiffman would throw me over the edge, because it's
comedy/tragedy of errors, but I'm learning "important" things at the same
time.... It's like elective surgery with insufficient anaesthetic.
And, take a pre-emptive Advil for this one...
https://www.youtube.com/watch?v=YueAtA_YnSY
> I am not convinced that this property is directly relevant to the
> problem I am trying to solve. I still think the key is in that quartic
> equation I came up with, which should not require numerical methods
> (beyond what's implicit in POV-Ray's built-in functions). The problem
> is that I am not practiced in solving quartic equations.
Dumb question, but is there an online solver?
A language with the proper symbolic logic?
Cheat and get the right answer first, then use that knowledge as a light to
guide you along the path of working out the quartic.
> P.S. I have known since 2007 that there is no exact formula for an
> ellipse's circumference. I discovered that while trying to weld this
> 'O' to the rectangular plate using an ellipse made out of blobs.
It's always the "simple" things, isn't it?
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Le 22/09/2020 à 12:28, Bald Eagle a écrit :
> Cousin Ricky <ric### [at] yahoocom> wrote:
>> I am not convinced that this property is directly relevant to the
>> problem I am trying to solve. I still think the key is in that quartic
>> equation I came up with, which should not require numerical methods
>> (beyond what's implicit in POV-Ray's built-in functions). The problem
>> is that I am not practiced in solving quartic equations.
>
> Dumb question, but is there an online solver?
Sir, Yes Sir !
mathworld wolfram (alpha) has such beast.
It take a bit of learning to get it do what is desired, but there is
some examples along the pages.
You can ask it to refactor, solve (even based on chosen parameters), and
far more.
We are more in algebra than geometry.
https://www.wolframalpha.com/examples/mathematics/algebra/
> A language with the proper symbolic logic?
>
> Cheat and get the right answer first, then use that knowledge as a light to
> guide you along the path of working out the quartic.
>
I think the elliptical torus with a minor radius of 0 should match the
equation of the ellipse.
That's the basic check of any solution: minor radius of 0 would simplify
the equation to an ellipse.
The difficulty is going backward: reintroduce a non-0 minor radius.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Le 21/09/2020 à 00:24, Bald Eagle a écrit :
> I just stumbled across this while trying to regain my sanity,
> and if even Ramanujan couldn't come up with anything but an approximation, than
> I think the rest of us are Fuuuuuuuuuuuuuuuuuuuuuumbling around in the dark.
>
> :)
>
> https://www.youtube.com/watch?v=5nW3nJhBHL0
>
> But don't anyone think that that will stop us from making another attempt, using
> new inspiration and mathematical tools!
>
> I think the above implies that due to the interesting properties of ellipses,
> that a workable solution will use numerical methods.
>
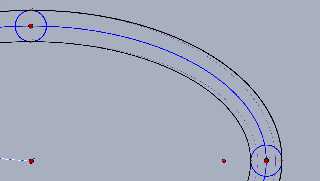
I tried to play a bit with the hope to transform the quartic equation of
circular torus into elliptical torus.
From (sqrt(x²+y²)-R)²+z²=r², replacing x²+y²=R² with (x/a)²+(y/b)²=1
And it is deception.
x^4/a^4
+ (2 x^2 y^2)/(a^2 b²)
- (2 r^2 x^2)/a²- (2 x^2)/a²
+ (2 x^2 z^2)/a²
+ y^4/b⁴
- (2 r^2 y^2)/b²- (2 y^2)/b²
+ (2 y^2 z^2)/b²
+ r⁴- 2 r²+ 1
- 2 r^2 z²+ 2 z²
+ z⁴
Because the scaling of x & y also influence the radius of the minor circle.
But it must be possible to have it with a 4th degree poly.
If F( Point ) is such polynomial, we have the following requirement
F( 0, +/- B , +/- Minor ) = 0 (point B)
F( +/- A, 0, +/- Minor ) = 0 (point A)
F( 0, +/- B +/- Minor, 0 ) = 0 (points M & N)
F( +/- A +/- Minor, 0, 0 ) = 0 (points K & L)
I guess, but cannot yet assert, that to avoid compressing the minor
circle, the z⁴, x⁴ and y⁴ must be 1.
And there might be some non-traditional power of x,y and z (aka odd) in
the non-null coefficient, which would disappear when A=B to have a
continuity with the circular torus.
Also, any point W On the central ellipse with z=+/- Minor is also F(W)=0
And if any more point is needed, there is the two minor circle at A & B
to explore more deeply than K, L, M & N.
Is that enough to try some spreadsheet solver, and how to do it ?
Post a reply to this message
Attachments:
Download 'torusellipse.png' (91 KB)
Preview of image 'torusellipse.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
So....
After the whole "surround a function with a tube" got explored (and still not
completely sorted out in my head), my brain decided to alert me that therein
might lay the possible solution to this problem.
I copy-pasted some code, fought with Phi again, "won", and got an elliptical
shaped torus. For a=2, b=1.5 it looked good, but the problem had always been
the eccentric tori. a=4 and b=0.75 revealed the same old problem.
I can't find the thread where you list the required specifications, but I don't
think that it's possible using a cross-sectional circle of a constant radius.
Because that's what we're doing with the tube method. And this doesn't give
inner and outer curves that are themselves ellipses.
https://www.frassek.org/3d-mathe/funktionsgraph-als-rohr-r%C3%B6hre/
https://image.jimcdn.com/app/cms/image/transf/dimension=1920x400:format=gif/path/scee86bccd27a6ab2/image/i16edd265f402b
f7c/version/1580469937/image.gif
We can get signed distance functions,
https://iquilezles.org/articles/distfunctions2d/
https://www.shadertoy.com/view/4sS3zz
and we know that we can calculate the tangent and normal vectors to the central
ellipse.
What I'm thinking right now is that we can ditch trying to create the whole
surface and focus on the 3 ellipses - the central, and the inner and outer. If
the inner and outer aren't the same distance away from the central curve along
the normal vector, then I'd say that this demonstrates that a solution isn't
possible, given the parameters.
I think I ran into this issue with Mike Horvath wanting ellipsoid shells -
simply scaling an ellipsoid doesn't give a constant-distance shell from the
original ellipsoid. But those ARE ellipsoids themselves. And calculating a
constant-distance shell would give objects that WEREN'T ellipsoids.
I'mm betting that those level sets of the signed distance function of an ellipse
- aren't ellipses.
So I think that some of the constraints are mutually exclusive.
Post a reply to this message
Attachments:
Download 'tubememe.jpg' (71 KB)
Preview of image 'tubememe.jpg'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
"Bald Eagle" <cre### [at] netscapenet> wrote:
> https://www.shadertoy.com/view/4sS3zz
Referenced in that code is this article with some comprehensive treatment of the
quartic equation.
https://iquilezles.org/articles/ellipsedist/
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
|
|
