|
 |
kurtz le pirate <kur### [at] gmail com> wrote:
> On 26/12/2021 03:00, Tor Olav Kristensen wrote:
> >> ...
> >
> >> Here, one sample of f(z) = (-z^3 + iz^2 + 1) / (z - 1 + i)^2.
> >
> > ...
> >
> > I'm a bit worried though, because my renderings of that function is quite
> > different from mine.
>
> Sorry, I put the wrong picture :(
> here, it's the good one.
>
> > What is your rendering showing ?
> > The magnitude, the real part or the imaginary part ? - or something else ?
>
> let z = a + ib
> f(z) = c +i d
>
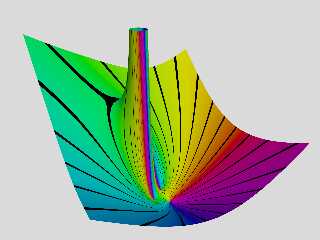
> Represented in POV in this way :
> a >> x axis
> b >> z axis
>
> arg(c + id) >> the color in HSL space with H = arg and L = logaritmic
> function of module between 0 and 1.
>
> module(c + id) >> y axis with a logarithmic scale
Ok, I see.
I've attached a similar rendering that I just I made of that function.
This time I've used used a mesh2 for the surface and added some black 1.5
degrees wide lines at 15 degrees intervals for the phase.
As you can see, the pole and the zeros seem to be located in a similar pattern,
but the area around the pole seems to be quite different.
I've tried to verify the functions I've created by feeding expressions to
Wolfram Alpha, like this:
https://www.wolframalpha.com/input/?i=%28-%283-4*i%29%5E3%2B%283-4*i%29%5E2*i%2B1%29%2F%28%283-4*i%29-1%2Bi%29%5E2
For the values of Z that I've tried, the results are the same as mine.
Perhaps you could do the same and compare with the results from your macros (?)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
> On 26/12/2021 03:00, Tor Olav Kristensen wrote:
> >> ...
> >
> >> Here, one sample of f(z) = (-z^3 + iz^2 + 1) / (z - 1 + i)^2.
> >
> > ...
> >
> > I'm a bit worried though, because my renderings of that function is quite
> > different from mine.
>
> Sorry, I put the wrong picture :(
> here, it's the good one.
>
> > What is your rendering showing ?
> > The magnitude, the real part or the imaginary part ? - or something else ?
>
> let z = a + ib
> f(z) = c +i d
>
> Represented in POV in this way :
> a >> x axis
> b >> z axis
>
> arg(c + id) >> the color in HSL space with H = arg and L = logaritmic
> function of module between 0 and 1.
>
> module(c + id) >> y axis with a logarithmic scale
Ok, I see.
I've attached a similar rendering that I just I made of that function.
This time I've used used a mesh2 for the surface and added some black 1.5
degrees wide lines at 15 degrees intervals for the phase.
As you can see, the pole and the zeros seem to be located in a similar pattern,
but the area around the pole seems to be quite different.
I've tried to verify the functions I've created by feeding expressions to
Wolfram Alpha, like this:
https://www.wolframalpha.com/input/?i=%28-%283-4*i%29%5E3%2B%283-4*i%29%5E2*i%2B1%29%2F%28%283-4*i%29-1%2Bi%29%5E2
For the values of Z that I've tried, the results are the same as mine.
Perhaps you could do the same and compare with the results from your macros (?)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
Attachments:
Download 'klps function.png' (396 KB)
Preview of image 'klps function.png'
|
 |




![]()