 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
So, since my whole Reorient_Triangle macro relies on the Reorient_Trans macro,
which was a bit of a black box operation, I decided to take a deeper look into
what goes on there, and unravel it all until I understood how it works.
The best I can describe it, briefly, is that we can look at POV-space as a
common reference frame that both Axis1 and Axis 2 exist in relation to.
Then we construct localized orthonormal (perpendicular) spaces using each Axis
argument as the x-axis of its frame.
We apply the Axis1 frame as a matrix transform to align it with POV-space.
Then we apply the _inverse_ of the matrix for Axis2 to do a reverse form of what
we just did for Axis1.
We align POV-space with the Axis2 frame by applying its matrix transpose.
(Which, since it's essentially a rotation matrix, is the same as the inverse)
Here's the original macro with some of the variables renamed, and plenty of
commentary.
I did note that half of the macro doesn't seem to even need to be there.
I'm gonna write an alternate form of the macro that uses the inverse keyword
just to make sure it does exactly the same thing.
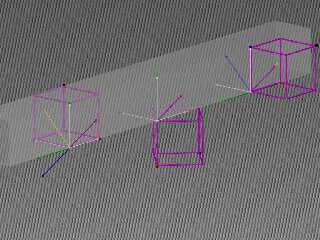
In the render, the left cube shows Axis1 in yellow, Axis2 in purple, and the
POV-space reference frame in white. The two perpendicular axes of the Axis1
frame are in green and blue.
At the center, we can see that the Axis 1 frame has been aligned with POV-space.
(I know it looks weird, and I spent a few hours working through a lot of
experiments, but since we're essentially applying a rotation transformation in
the negative direction around x, the first transform winds up doing that wild
flip to invert the shape. Look at the relationship between the perpendiculars
and the cube, and it ought to make sense)
Now we need to align the x-vector with Axis2, and you can imagine a rotation
aroind -x, followed by a rotation around -z to get there. And that aligns
everything.
If you picture the shortest-path rotation from Axis1 to Axis2, you'll see that
the colored corner markers end up in the right place, which was one of the
things I was concerned about, and spurred this whole venture.
//############################################################################
#macro Reorient_Trans (Axis1, Axis2)
// Edited and commented by Bill Walker "Bald Eagle" Feb 2024
#local Vec_1 = vnormalize (Axis1);
#local Vec_2 = vnormalize (Axis2);
// vcross returns a perpendicular vector
// if vectors are parallel or antiparallel, then vcross = 0
#local Perp = vcross (Vec_1, Vec_2);
#if (vlength (Perp) > 0)
#local Pboth = vnormalize (Perp);
// so now we have normalized vectors with a common
// perpendicular to both vectors "Perp"
// We generate a third perpendicular vector for each
// reference frame, "Perp1" and "Perp2"
#local Perp1 = vnormalize (vcross (Vec_1, Pboth));
#local Perp2 = vnormalize (vcross (Vec_2, Pboth));
transform {
// Now we transform the basis vectors.
// Notice that the standard matrix is composed of COLUMN vectors
// All of the vectors are normalized, and they
// are all orthonormal (perpendicular to each other)
// so this constitutes a rigid body transformation
// which only performs rotations
// former x vector gets aligned to Vec_1 (Axis1)
// former y vector gets aligned with the common perpendicular Pboth
// former z vector gets aligned to Perp1
matrix <
Vec_1.x, Pboth.x, Perp1.x,
Vec_1.y, Pboth.y, Perp1.y,
Vec_1.z, Pboth.z, Perp1.z,
0, 0, 0 >
// Notice that the following matrix is composed of ROW vectors
// So this is a transpose matrix
// We know it's an orthonormal rotation matrix (with a determinant of 1)
// so the matrix transpose is actually the same as the matrix inverse
// Let's consider what the untransposed matrix would have done:
// former x vector gets aligned to Vec_2 (Axis2)
// former y vector gets aligned with the common perpendicular Pboth
// former z vector gets aligned to Perp2
// (Just like the first matrix)
// So we would have taken the result we're aiming toward - an alignment with
Axis2,
// and aligning it to the same place as we have just moved our starting Axis1
to.
// And since the transpose matrix is the INVERSE, we are just UNDOING that
transform
// to move the common reference frame to that of Axis2
// Presumably we could have accomplished the same operation with the standard
column
// major form using a separate "transform { matrix <> inverse}" statement
matrix <
Vec_2.x, Vec_2.y, Vec_2.z,
Pboth.x, Pboth.y, Pboth.z,
Perp2.x, Perp2.y, Perp2.z,
0, 0, 0 >
}
#else
// This makes no sense to me, since Vec_1 and Vec_2 are both normalized
vectors,
// so the length of one unit vector minus another unit vector will ALWAYS be
zero
#if (vlength (Vec_1-Vec_2) = 0)
transform {}
#else
// Which means that this part NEVER gets executed
#local vZ = VPerp_To_Vector (Vec_2);
transform {Axis_Rotate_Trans (vZ, 180)}
#end
#end
#end
Post a reply to this message
Attachments:
Download 'reorient_trans_viz.png' (748 KB)
Preview of image 'reorient_trans_viz.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> I'm gonna write an alternate form of the macro that uses the inverse keyword
> just to make sure it does exactly the same thing.
And indeed, using the following gives the same results.
Note that you have to enclose the second matrix in its own transform {}, else
the inverse gets applied to the whole 2-matrix transform instead of just the
second matrix.
transform {
matrix <
Vec_1.x, Pboth.x, Perp1.x,
Vec_1.y, Pboth.y, Perp1.y,
Vec_1.z, Pboth.z, Perp1.z,
0, 0, 0 >
transform {
// Column vectors like above
matrix <
Vec_2.x, Pboth.x, Perp2.x,
Vec_2.y, Pboth.y, Perp2.y,
Vec_2.z, Pboth.z, Perp2.z,
0, 0, 0 >
inverse // <--- Inverse
}
} net> wrote:
> I'm gonna write an alternate form of the macro that uses the inverse keyword
> just to make sure it does exactly the same thing.
And indeed, using the following gives the same results.
Note that you have to enclose the second matrix in its own transform {}, else
the inverse gets applied to the whole 2-matrix transform instead of just the
second matrix.
transform {
matrix <
Vec_1.x, Pboth.x, Perp1.x,
Vec_1.y, Pboth.y, Perp1.y,
Vec_1.z, Pboth.z, Perp1.z,
0, 0, 0 >
transform {
// Column vectors like above
matrix <
Vec_2.x, Pboth.x, Perp2.x,
Vec_2.y, Pboth.y, Perp2.y,
Vec_2.z, Pboth.z, Perp2.z,
0, 0, 0 >
inverse // <--- Inverse
}
}
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
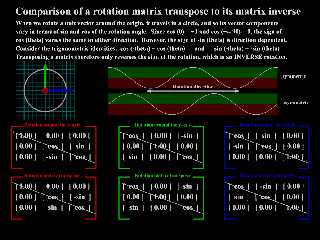
> (Which, since it's essentially a rotation matrix, is the same as the inverse)
I reworked my old rotation matrices scene to give a bit more of a visual
interpretation.
I wasn't sure if I'd need to animate this, and have changing values on a
readout, or the transformed vector rendered alongside its inverse and
transpose...
Hopefully it's clear, if it's not, then let me know what would really help
illustrate the concept(s) more clearly.
- BW net> wrote:
> (Which, since it's essentially a rotation matrix, is the same as the inverse)
I reworked my old rotation matrices scene to give a bit more of a visual
interpretation.
I wasn't sure if I'd need to animate this, and have changing values on a
readout, or the transformed vector rendered alongside its inverse and
transpose...
Hopefully it's clear, if it's not, then let me know what would really help
illustrate the concept(s) more clearly.
- BW
Post a reply to this message
Attachments:
Download 'matrixtranspose.png' (190 KB)
Preview of image 'matrixtranspose.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> So, since my whole Reorient_Triangle macro relies on the Reorient_Trans macro,
> which was a bit of a black box operation, I decided to take a deeper look into
> what goes on there, and unravel it all until I understood how it works.
>
> The best I can describe it, briefly, is that we can look at POV-space as a
> common reference frame that both Axis1 and Axis 2 exist in relation to.
> Then we construct localized orthonormal (perpendicular) spaces using each Axis
> argument as the x-axis of its frame.
>
> We apply the Axis1 frame as a matrix transform to align it with POV-space.
> Then we apply the _inverse_ of the matrix for Axis2 to do a reverse form of what
> we just did for Axis1.
> We align POV-space with the Axis2 frame by applying its matrix transpose.
> (Which, since it's essentially a rotation matrix, is the same as the inverse)
>
> Here's the original macro with some of the variables renamed, and plenty of
> commentary.
>
> I did note that half of the macro doesn't seem to even need to be there.
>
> I'm gonna write an alternate form of the macro that uses the inverse keyword
> just to make sure it does exactly the same thing.
>
> In the render, the left cube shows Axis1 in yellow, Axis2 in purple, and the
> POV-space reference frame in white. The two perpendicular axes of the Axis1
> frame are in green and blue.
>
> At the center, we can see that the Axis 1 frame has been aligned with POV-space.
> (I know it looks weird, and I spent a few hours working through a lot of
> experiments, but since we're essentially applying a rotation transformation in
> the negative direction around x, the first transform winds up doing that wild
> flip to invert the shape. Look at the relationship between the perpendiculars
> and the cube, and it ought to make sense)
>
> Now we need to align the x-vector with Axis2, and you can imagine a rotation
> aroind -x, followed by a rotation around -z to get there. And that aligns
> everything.
>
> If you picture the shortest-path rotation from Axis1 to Axis2, you'll see that
> the colored corner markers end up in the right place, which was one of the
> things I was concerned about, and spurred this whole venture.
>
> //############################################################################
>
>
> #macro Reorient_Trans (Axis1, Axis2)
> // Edited and commented by Bill Walker "Bald Eagle" Feb 2024
> #local Vec_1 = vnormalize (Axis1);
> #local Vec_2 = vnormalize (Axis2);
> // vcross returns a perpendicular vector
> // if vectors are parallel or antiparallel, then vcross = 0
> #local Perp = vcross (Vec_1, Vec_2);
> #if (vlength (Perp) > 0)
> #local Pboth = vnormalize (Perp);
> // so now we have normalized vectors with a common
> // perpendicular to both vectors "Perp"
> // We generate a third perpendicular vector for each
> // reference frame, "Perp1" and "Perp2"
> #local Perp1 = vnormalize (vcross (Vec_1, Pboth));
> #local Perp2 = vnormalize (vcross (Vec_2, Pboth));
>
> transform {
> // Now we transform the basis vectors.
> // Notice that the standard matrix is composed of COLUMN vectors
> // All of the vectors are normalized, and they
> // are all orthonormal (perpendicular to each other)
> // so this constitutes a rigid body transformation
> // which only performs rotations
> // former x vector gets aligned to Vec_1 (Axis1)
> // former y vector gets aligned with the common perpendicular Pboth
> // former z vector gets aligned to Perp1
>
> matrix <
> Vec_1.x, Pboth.x, Perp1.x,
> Vec_1.y, Pboth.y, Perp1.y,
> Vec_1.z, Pboth.z, Perp1.z,
> 0, 0, 0 >
>
> // Notice that the following matrix is composed of ROW vectors
> // So this is a transpose matrix
> // We know it's an orthonormal rotation matrix (with a determinant of 1)
> // so the matrix transpose is actually the same as the matrix inverse
>
> // Let's consider what the untransposed matrix would have done:
> // former x vector gets aligned to Vec_2 (Axis2)
> // former y vector gets aligned with the common perpendicular Pboth
> // former z vector gets aligned to Perp2
> // (Just like the first matrix)
>
> // So we would have taken the result we're aiming toward - an alignment with
> Axis2,
> // and aligning it to the same place as we have just moved our starting Axis1
> to.
> // And since the transpose matrix is the INVERSE, we are just UNDOING that
> transform
> // to move the common reference frame to that of Axis2
>
> // Presumably we could have accomplished the same operation with the standard
> column
> // major form using a separate "transform { matrix <> inverse}" statement
>
> matrix <
> Vec_2.x, Vec_2.y, Vec_2.z,
> Pboth.x, Pboth.y, Pboth.z,
> Perp2.x, Perp2.y, Perp2.z,
> 0, 0, 0 >
> }
> #else
> // This makes no sense to me, since Vec_1 and Vec_2 are both normalized
> vectors,
> // so the length of one unit vector minus another unit vector will ALWAYS be
> zero
> #if (vlength (Vec_1-Vec_2) = 0)
> transform {}
> #else
> // Which means that this part NEVER gets executed
> #local vZ = VPerp_To_Vector (Vec_2);
> transform {Axis_Rotate_Trans (vZ, 180)}
> #end
> #end
> #end
Hi Bill
It's a useful exercise you've started here.
You may also want to have a look at the ReorientTransform() macro here:
https://github.com/t-o-k/Useful-POV-Ray-macros/blob/main/vectors.inc
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
> So, since my whole Reorient_Triangle macro relies on the Reorient_Trans macro,
> which was a bit of a black box operation, I decided to take a deeper look into
> what goes on there, and unravel it all until I understood how it works.
>
> The best I can describe it, briefly, is that we can look at POV-space as a
> common reference frame that both Axis1 and Axis 2 exist in relation to.
> Then we construct localized orthonormal (perpendicular) spaces using each Axis
> argument as the x-axis of its frame.
>
> We apply the Axis1 frame as a matrix transform to align it with POV-space.
> Then we apply the _inverse_ of the matrix for Axis2 to do a reverse form of what
> we just did for Axis1.
> We align POV-space with the Axis2 frame by applying its matrix transpose.
> (Which, since it's essentially a rotation matrix, is the same as the inverse)
>
> Here's the original macro with some of the variables renamed, and plenty of
> commentary.
>
> I did note that half of the macro doesn't seem to even need to be there.
>
> I'm gonna write an alternate form of the macro that uses the inverse keyword
> just to make sure it does exactly the same thing.
>
> In the render, the left cube shows Axis1 in yellow, Axis2 in purple, and the
> POV-space reference frame in white. The two perpendicular axes of the Axis1
> frame are in green and blue.
>
> At the center, we can see that the Axis 1 frame has been aligned with POV-space.
> (I know it looks weird, and I spent a few hours working through a lot of
> experiments, but since we're essentially applying a rotation transformation in
> the negative direction around x, the first transform winds up doing that wild
> flip to invert the shape. Look at the relationship between the perpendiculars
> and the cube, and it ought to make sense)
>
> Now we need to align the x-vector with Axis2, and you can imagine a rotation
> aroind -x, followed by a rotation around -z to get there. And that aligns
> everything.
>
> If you picture the shortest-path rotation from Axis1 to Axis2, you'll see that
> the colored corner markers end up in the right place, which was one of the
> things I was concerned about, and spurred this whole venture.
>
> //############################################################################
>
>
> #macro Reorient_Trans (Axis1, Axis2)
> // Edited and commented by Bill Walker "Bald Eagle" Feb 2024
> #local Vec_1 = vnormalize (Axis1);
> #local Vec_2 = vnormalize (Axis2);
> // vcross returns a perpendicular vector
> // if vectors are parallel or antiparallel, then vcross = 0
> #local Perp = vcross (Vec_1, Vec_2);
> #if (vlength (Perp) > 0)
> #local Pboth = vnormalize (Perp);
> // so now we have normalized vectors with a common
> // perpendicular to both vectors "Perp"
> // We generate a third perpendicular vector for each
> // reference frame, "Perp1" and "Perp2"
> #local Perp1 = vnormalize (vcross (Vec_1, Pboth));
> #local Perp2 = vnormalize (vcross (Vec_2, Pboth));
>
> transform {
> // Now we transform the basis vectors.
> // Notice that the standard matrix is composed of COLUMN vectors
> // All of the vectors are normalized, and they
> // are all orthonormal (perpendicular to each other)
> // so this constitutes a rigid body transformation
> // which only performs rotations
> // former x vector gets aligned to Vec_1 (Axis1)
> // former y vector gets aligned with the common perpendicular Pboth
> // former z vector gets aligned to Perp1
>
> matrix <
> Vec_1.x, Pboth.x, Perp1.x,
> Vec_1.y, Pboth.y, Perp1.y,
> Vec_1.z, Pboth.z, Perp1.z,
> 0, 0, 0 >
>
> // Notice that the following matrix is composed of ROW vectors
> // So this is a transpose matrix
> // We know it's an orthonormal rotation matrix (with a determinant of 1)
> // so the matrix transpose is actually the same as the matrix inverse
>
> // Let's consider what the untransposed matrix would have done:
> // former x vector gets aligned to Vec_2 (Axis2)
> // former y vector gets aligned with the common perpendicular Pboth
> // former z vector gets aligned to Perp2
> // (Just like the first matrix)
>
> // So we would have taken the result we're aiming toward - an alignment with
> Axis2,
> // and aligning it to the same place as we have just moved our starting Axis1
> to.
> // And since the transpose matrix is the INVERSE, we are just UNDOING that
> transform
> // to move the common reference frame to that of Axis2
>
> // Presumably we could have accomplished the same operation with the standard
> column
> // major form using a separate "transform { matrix <> inverse}" statement
>
> matrix <
> Vec_2.x, Vec_2.y, Vec_2.z,
> Pboth.x, Pboth.y, Pboth.z,
> Perp2.x, Perp2.y, Perp2.z,
> 0, 0, 0 >
> }
> #else
> // This makes no sense to me, since Vec_1 and Vec_2 are both normalized
> vectors,
> // so the length of one unit vector minus another unit vector will ALWAYS be
> zero
> #if (vlength (Vec_1-Vec_2) = 0)
> transform {}
> #else
> // Which means that this part NEVER gets executed
> #local vZ = VPerp_To_Vector (Vec_2);
> transform {Axis_Rotate_Trans (vZ, 180)}
> #end
> #end
> #end
Hi Bill
It's a useful exercise you've started here.
You may also want to have a look at the ReorientTransform() macro here:
https://github.com/t-o-k/Useful-POV-Ray-macros/blob/main/vectors.inc
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> "Bald Eagle" <cre### [at] netscape com> wrote:
> "Bald Eagle" <cre### [at] netscape net> wrote:
>...
>
> Hi Bill
>
> It's a useful exercise you've started here.
>
> You may also want to have a look at the ReorientTransform() macro here:
> https://github.com/t-o-k/Useful-POV-Ray-macros/blob/main/vectors.inc
And for axis rotate, this is relevant:
https://github.com/t-o-k/Rodrigues-rotation-formula
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
>...
>
> Hi Bill
>
> It's a useful exercise you've started here.
>
> You may also want to have a look at the ReorientTransform() macro here:
> https://github.com/t-o-k/Useful-POV-Ray-macros/blob/main/vectors.inc
And for axis rotate, this is relevant:
https://github.com/t-o-k/Rodrigues-rotation-formula
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> > "Bald Eagle" <cre### [at] netscape com> wrote:
> > "Bald Eagle" <cre### [at] netscape net> wrote:
> >...
> >
> > Hi Bill
> >
> > It's a useful exercise you've started here.
> >
> > You may also want to have a look at the ReorientTransform() macro here:
> > https://github.com/t-o-k/Useful-POV-Ray-macros/blob/main/vectors.inc
>
>
> And for axis rotate, this is relevant:
>
> https://github.com/t-o-k/Rodrigues-rotation-formula
>
Some more here:
From: Tor Olav Kristensen
Subject: Rotation around an arbitrary axis
Date: 2001-11-29 19:23:16
https://news.povray.org/povray.advanced-users/thread/%3C3C06D0B8.9DE747A0%40hotmail.com%3E/
- and here:
https://github.com/t-o-k/scikit-vectors/blob/master/skvectors/cartesian_3d_vectors.py
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
> >...
> >
> > Hi Bill
> >
> > It's a useful exercise you've started here.
> >
> > You may also want to have a look at the ReorientTransform() macro here:
> > https://github.com/t-o-k/Useful-POV-Ray-macros/blob/main/vectors.inc
>
>
> And for axis rotate, this is relevant:
>
> https://github.com/t-o-k/Rodrigues-rotation-formula
>
Some more here:
From: Tor Olav Kristensen
Subject: Rotation around an arbitrary axis
Date: 2001-11-29 19:23:16
https://news.povray.org/povray.advanced-users/thread/%3C3C06D0B8.9DE747A0%40hotmail.com%3E/
- and here:
https://github.com/t-o-k/scikit-vectors/blob/master/skvectors/cartesian_3d_vectors.py
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thanks Tor!
You've got an endless library of really useful macros, as usual.
With regard to matrix methods, would you happen to have any words of wisdom
about how to go about the following with matrices as opposed to my vector math
way?
http://news.povray.org/povray.binaries.images/message/%3Cweb.65c027a941c066f01f9dae3025979125%40news.povray.org%3E/#%3C
web.65c027a941c066f01f9dae3025979125%40news.povray.org%3E
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> // This makes no sense to me, since Vec_1 and Vec_2 are both normalized
> vectors,
> // so the length of one unit vector minus another unit vector will ALWAYS be
> zero
> #if (vlength (Vec_1-Vec_2) = 0)
> transform {}
> #else
> // Which means that this part NEVER gets executed
> #local vZ = VPerp_To_Vector (Vec_2);
> transform {Axis_Rotate_Trans (vZ, 180)}
>...
IIRC it was me that added those two if-then-else parts to John VanSickle's
reorient macro.
Note that we are subtracting the normalized vectors, not their lengths.
And then we check if the resulting vector has zero length.
So no, one unit vector minus another unit vector will NOT ALWAYS be zero, only
if they are pointing the same direction, in which case no transformation is
necessary.
After the last else statement we can be sure that the two vectors are pointing
in opposite directions. In this case the math for calculating the components of
the reorient matrix breaks down.
In this case we can not know what the user actually want to achieve. (And
perhaps she/he does not know this her/him-selves.)
We can (and perhaps we should) now give up and use the #error statement.
But in some cases we can choose one of infinitely many possible solutions and
the result will be the same (e.g. if the reoriented object is symmetric around a
line in the same direction as the the "reorient from" vector, like a cylinder.)
Now note that the reorient transform is very similar to the axis rotate
transform. If we take the cross product between the vector to reorient from and
the vector to reorient to, we get a rotation axis for the axis rotate transform.
And if we find the angle between those two vectors, (e.g. by acos of their dot
product, or arcsin of the length of their cross product, or both combined with
atan2, or a more numerical stable formula), we have the rotation angle for the
axis transform.
I choose one vector (from infinitely many vectors), that is perpendicular to
both the "rotate from" vector and the "rotate to" vector, to use for the axis in
the axis rotate transform. The rotation angle is 180 degrees.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
>...
> // This makes no sense to me, since Vec_1 and Vec_2 are both normalized
> vectors,
> // so the length of one unit vector minus another unit vector will ALWAYS be
> zero
> #if (vlength (Vec_1-Vec_2) = 0)
> transform {}
> #else
> // Which means that this part NEVER gets executed
> #local vZ = VPerp_To_Vector (Vec_2);
> transform {Axis_Rotate_Trans (vZ, 180)}
>...
IIRC it was me that added those two if-then-else parts to John VanSickle's
reorient macro.
Note that we are subtracting the normalized vectors, not their lengths.
And then we check if the resulting vector has zero length.
So no, one unit vector minus another unit vector will NOT ALWAYS be zero, only
if they are pointing the same direction, in which case no transformation is
necessary.
After the last else statement we can be sure that the two vectors are pointing
in opposite directions. In this case the math for calculating the components of
the reorient matrix breaks down.
In this case we can not know what the user actually want to achieve. (And
perhaps she/he does not know this her/him-selves.)
We can (and perhaps we should) now give up and use the #error statement.
But in some cases we can choose one of infinitely many possible solutions and
the result will be the same (e.g. if the reoriented object is symmetric around a
line in the same direction as the the "reorient from" vector, like a cylinder.)
Now note that the reorient transform is very similar to the axis rotate
transform. If we take the cross product between the vector to reorient from and
the vector to reorient to, we get a rotation axis for the axis rotate transform.
And if we find the angle between those two vectors, (e.g. by acos of their dot
product, or arcsin of the length of their cross product, or both combined with
atan2, or a more numerical stable formula), we have the rotation angle for the
axis transform.
I choose one vector (from infinitely many vectors), that is perpendicular to
both the "rotate from" vector and the "rotate to" vector, to use for the axis in
the axis rotate transform. The rotation angle is 180 degrees.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Thanks Tor!
>
> You've got an endless library of really useful macros, as usual.
Yes, I've written a lot of macros, some more useful than others.
My problem is to remember that I wrote them and were I've put them.
> With regard to matrix methods, would you happen to have any words of wisdom
> about how to go about the following with matrices as opposed to my vector math
> way?
>
>
http://news.povray.org/povray.binaries.images/message/%3Cweb.65c027a941c066f01f9dae3025979125%40news.povray.org%3E/#%
3C
> web.65c027a941c066f01f9dae3025979125%40news.povray.org%3E
I just had a quick peek at your code.
It seems healthy, although it can probably be slimmed down a bit.
I'll see of can find some spare time for commenting it in the coming days.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
> Thanks Tor!
>
> You've got an endless library of really useful macros, as usual.
Yes, I've written a lot of macros, some more useful than others.
My problem is to remember that I wrote them and were I've put them.
> With regard to matrix methods, would you happen to have any words of wisdom
> about how to go about the following with matrices as opposed to my vector math
> way?
>
>
http://news.povray.org/povray.binaries.images/message/%3Cweb.65c027a941c066f01f9dae3025979125%40news.povray.org%3E/#%
3C
> web.65c027a941c066f01f9dae3025979125%40news.povray.org%3E
I just had a quick peek at your code.
It seems healthy, although it can probably be slimmed down a bit.
I'll see of can find some spare time for commenting it in the coming days.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 08/02/2024 om 18:54 schreef Bald Eagle:
>
> So, since my whole Reorient_Triangle macro relies on the Reorient_Trans macro,
> which was a bit of a black box operation, I decided to take a deeper look into
> what goes on there, and unravel it all until I understood how it works.
>
Before I go further in reading: This is a very welcome exercise you have
started here, Bill! I am a very regular user of the macro and I confess
that I have had a lot of misunderstandings about its working in the past.
Keep on the good work!
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()