|
 |
So, since my whole Reorient_Triangle macro relies on the Reorient_Trans macro,
which was a bit of a black box operation, I decided to take a deeper look into
what goes on there, and unravel it all until I understood how it works.
The best I can describe it, briefly, is that we can look at POV-space as a
common reference frame that both Axis1 and Axis 2 exist in relation to.
Then we construct localized orthonormal (perpendicular) spaces using each Axis
argument as the x-axis of its frame.
We apply the Axis1 frame as a matrix transform to align it with POV-space.
Then we apply the _inverse_ of the matrix for Axis2 to do a reverse form of what
we just did for Axis1.
We align POV-space with the Axis2 frame by applying its matrix transpose.
(Which, since it's essentially a rotation matrix, is the same as the inverse)
Here's the original macro with some of the variables renamed, and plenty of
commentary.
I did note that half of the macro doesn't seem to even need to be there.
I'm gonna write an alternate form of the macro that uses the inverse keyword
just to make sure it does exactly the same thing.
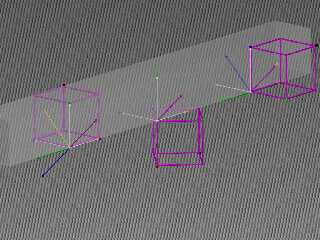
In the render, the left cube shows Axis1 in yellow, Axis2 in purple, and the
POV-space reference frame in white. The two perpendicular axes of the Axis1
frame are in green and blue.
At the center, we can see that the Axis 1 frame has been aligned with POV-space.
(I know it looks weird, and I spent a few hours working through a lot of
experiments, but since we're essentially applying a rotation transformation in
the negative direction around x, the first transform winds up doing that wild
flip to invert the shape. Look at the relationship between the perpendiculars
and the cube, and it ought to make sense)
Now we need to align the x-vector with Axis2, and you can imagine a rotation
aroind -x, followed by a rotation around -z to get there. And that aligns
everything.
If you picture the shortest-path rotation from Axis1 to Axis2, you'll see that
the colored corner markers end up in the right place, which was one of the
things I was concerned about, and spurred this whole venture.
//############################################################################
#macro Reorient_Trans (Axis1, Axis2)
// Edited and commented by Bill Walker "Bald Eagle" Feb 2024
#local Vec_1 = vnormalize (Axis1);
#local Vec_2 = vnormalize (Axis2);
// vcross returns a perpendicular vector
// if vectors are parallel or antiparallel, then vcross = 0
#local Perp = vcross (Vec_1, Vec_2);
#if (vlength (Perp) > 0)
#local Pboth = vnormalize (Perp);
// so now we have normalized vectors with a common
// perpendicular to both vectors "Perp"
// We generate a third perpendicular vector for each
// reference frame, "Perp1" and "Perp2"
#local Perp1 = vnormalize (vcross (Vec_1, Pboth));
#local Perp2 = vnormalize (vcross (Vec_2, Pboth));
transform {
// Now we transform the basis vectors.
// Notice that the standard matrix is composed of COLUMN vectors
// All of the vectors are normalized, and they
// are all orthonormal (perpendicular to each other)
// so this constitutes a rigid body transformation
// which only performs rotations
// former x vector gets aligned to Vec_1 (Axis1)
// former y vector gets aligned with the common perpendicular Pboth
// former z vector gets aligned to Perp1
matrix <
Vec_1.x, Pboth.x, Perp1.x,
Vec_1.y, Pboth.y, Perp1.y,
Vec_1.z, Pboth.z, Perp1.z,
0, 0, 0 >
// Notice that the following matrix is composed of ROW vectors
// So this is a transpose matrix
// We know it's an orthonormal rotation matrix (with a determinant of 1)
// so the matrix transpose is actually the same as the matrix inverse
// Let's consider what the untransposed matrix would have done:
// former x vector gets aligned to Vec_2 (Axis2)
// former y vector gets aligned with the common perpendicular Pboth
// former z vector gets aligned to Perp2
// (Just like the first matrix)
// So we would have taken the result we're aiming toward - an alignment with
Axis2,
// and aligning it to the same place as we have just moved our starting Axis1
to.
// And since the transpose matrix is the INVERSE, we are just UNDOING that
transform
// to move the common reference frame to that of Axis2
// Presumably we could have accomplished the same operation with the standard
column
// major form using a separate "transform { matrix <> inverse}" statement
matrix <
Vec_2.x, Vec_2.y, Vec_2.z,
Pboth.x, Pboth.y, Pboth.z,
Perp2.x, Perp2.y, Perp2.z,
0, 0, 0 >
}
#else
// This makes no sense to me, since Vec_1 and Vec_2 are both normalized
vectors,
// so the length of one unit vector minus another unit vector will ALWAYS be
zero
#if (vlength (Vec_1-Vec_2) = 0)
transform {}
#else
// Which means that this part NEVER gets executed
#local vZ = VPerp_To_Vector (Vec_2);
transform {Axis_Rotate_Trans (vZ, 180)}
#end
#end
#end
Post a reply to this message
Attachments:
Download 'reorient_trans_viz.png' (748 KB)
Preview of image 'reorient_trans_viz.png'
|
 |




![]()