|
 |
I was interested in using a lemon, or the inner surface of a spindle torus, or
the surface of revolution of a vesica piscis - whichever terminology you prefer
- to compare to a surface.
There is precious little information that I can find describing the lemon, and I
wanted a parameterized object.
The documentation doesn't have a diagram of how the lemon {} available in
version 3.8 is constructed (like it does for the ovus {} ), and the explanation
took me longer than it should have to clearly understand.
https://wiki.povray.org/content/Reference:Lemon
https://wiki.povray.org/content/Reference:Ovus
Presently, I have two problems. And one other issue.
First, when I try to render the lemon {} object with the current parameters, I
only get a very faint speckling rather than a well-formed surface. (I have
rendered several successful test lemons in 3.8)
You can just see it in the render. This makes me sad, as I know Jerome Grimbert
did a lot of work on this shape.
Second, after I finally worked out how to isolate the inner surface of a
standard torus using an isosurface, I found that I needed to add a Fudgefactor
to the minor radius in order to remove a lot of artefactual noise. I found the
0.2 magnitude of the FudgeFactor to be disturbingly large.
(Maybe I would have better luck with a polynomial object.)
The other issue is that the isosurface seems to have the interior_texture on the
outside, and the texture on the inside.
Anyone have any ideas?
// -------------------------------------------------------------------------
#version 3.8;
global_settings {assumed_gamma 1}
#declare E = 0.00001;
#declare Zoom = 160;
camera {
orthographic
//angle
location <0, 0, -image_width*2>
right x*image_width/Zoom
up y*image_height/Zoom
//sky y
look_at <0, 0, 0>
rotate y*0
}
light_source {<image_width/2, image_height/2, -image_width*4> rgb 1 shadowless}
sky_sphere {pigment {rgb 1}}
#declare R = 3;
#declare r = 0.25;
#declare Line = 0.01;
#macro LemonLayout (Radius, Distance, Points)
#local Circle =
union {
sphere {0, Line*2}
torus {Radius, Line rotate x*90}
pigment {rgb x}
}
object {Circle translate x*Distance}
object {Circle translate -x*Distance}
#if (Points)
union {
#for (Phi, 0, tau, 0.1)
#for (Theta, 0, tau, 0.1)
#local X = Radius * cos (Theta) * sin (Phi) - Distance;
#if (X >= 0)
#local Y = Radius * sin (Theta);
#local Z = X * sin (Phi);
sphere {<X, Y, Z>, Line*2}
#end
#end
#end
pigment {rgb z}
}
#end
#end
#declare MF = 0.6;
#declare Min_factor= min (MF, 1);
#declare Max_gradient = 250;
#declare P0 = Max_gradient * Min_factor;
#declare P1 = sqrt (Max_gradient/(Max_gradient * Min_factor));
#declare _P2 = 0.7;
#declare P2 = min (_P2, 1);
#declare r = 1;
#declare R = 0.6;
// intersection points of 2 circles
// (x+R)(x+R) + y*y = r*r
// (x-R)(x-R) + y*y = r*r
// x*x + 2*R*x + R*R + y*y = r*r
// x*x - 2*R*x + R*R + y*y = r*r
// 4*R*x = 0
// x = 0
// y = sqrt ( r*r - R*R )
#declare Y = sqrt ( r*r - R*R );
#declare FudgeFactor = 0.2;
#declare Torus = function {pow (x*x + y*y + z*z + R*R - r*r, 2) -
4*R*R*(x*x+z*z)}
#declare Spindle = function {select ((r-R)*(r-R) - (x*x+z*z) + FudgeFactor, 0,
pow (x*x + y*y + z*z + R*R - r*r, 2) - 4*R*R*(x*x+z*z))}
#declare Iso =
isosurface {
function {Spindle (x, y, z)}
contained_by { box {<-(R-r), -Y, -(R-r)>, <R-r, Y, R-r>} } // container shape
accuracy 0.001
max_gradient 250
//evaluate P0, P1, P2
open
texture {
pigment {rgb z}
finish {specular 0.4}
} // end texture
interior_texture
{
pigment {rgb x+y}
finish {specular 0.4}
} // end texture
} // end isosurface
union {
LemonLayout (1, 0.6, no)
object {Iso }
translate -x*r
}
union {
LemonLayout (1, 0.6, no)
object {Iso}
rotate y*90 translate x*r
}
lemon {
<0, -Y, 0>, 0, <0, Y, 0>, 0, r
texture {pigment {rgb <0.2, 0.2,0>} finish {specular 0.4}}
sturm
}
Post a reply to this message
Attachments:
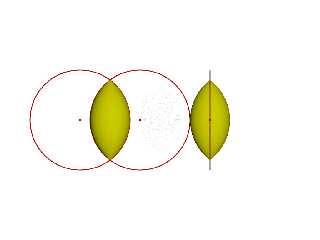
Download 'lemon.png' (57 KB)
Preview of image 'lemon.png'
|
 |




![]()