|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Aside from that, I'm thinking that it could work sort of like the way you've
> made carpets from image maps - we'd feed an object into a macro, and build a
> surface in a piecewise fashion based on that. The only way I can currently see
> doing that is using trace ().
>
> I have a scene where I can plot the entire Frenet-Serret frame for all the
> points on a Bezier surface just using trace (), but at the the moment, the
> results are probably only valid because the points are on an axis-aligned grid.
>
> The 2 vectors perpendicular to the normal give me the tangent and binormal,
> which I'm treating as du and dv, and I'm assuming that a normalized vector
> addition of those will give me duv. I still need the second partial derivatives
> to get the curvature - and I have no real idea how to get that numerically or
> geometrically except to do a sort of central differences type thing to assess
> the concavity/convexity at each point.
>
> No idea if any of that will work, but in typical fashion, I'll just plow ahead
> like a blind bull in a china shop, and see what else I can break. :D
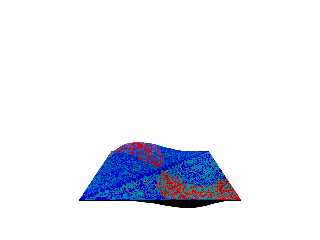
So, I rode the struggle bus and after a whole lot of plotting black spheres,
finally jiggled things so that I get some sort of color differentiation. I
suppose it very loosely resembles the Gaussian curvature render, so it's a step
in the right direction.
It's gonna need to store all of the results in an array so I can get the min &
max and normalize the result for the color map. But the biggest limitation is
of course the usual problems involving trace () - you just can't get into
overhangs and other occluded areas that the trace () ray hits first.
Probably gonna be one of those things where it's only good for Bezier patches
and parametric objects. Possibly isosurfaces. net> wrote:
> Aside from that, I'm thinking that it could work sort of like the way you've
> made carpets from image maps - we'd feed an object into a macro, and build a
> surface in a piecewise fashion based on that. The only way I can currently see
> doing that is using trace ().
>
> I have a scene where I can plot the entire Frenet-Serret frame for all the
> points on a Bezier surface just using trace (), but at the the moment, the
> results are probably only valid because the points are on an axis-aligned grid.
>
> The 2 vectors perpendicular to the normal give me the tangent and binormal,
> which I'm treating as du and dv, and I'm assuming that a normalized vector
> addition of those will give me duv. I still need the second partial derivatives
> to get the curvature - and I have no real idea how to get that numerically or
> geometrically except to do a sort of central differences type thing to assess
> the concavity/convexity at each point.
>
> No idea if any of that will work, but in typical fashion, I'll just plow ahead
> like a blind bull in a china shop, and see what else I can break. :D
So, I rode the struggle bus and after a whole lot of plotting black spheres,
finally jiggled things so that I get some sort of color differentiation. I
suppose it very loosely resembles the Gaussian curvature render, so it's a step
in the right direction.
It's gonna need to store all of the results in an array so I can get the min &
max and normalize the result for the color map. But the biggest limitation is
of course the usual problems involving trace () - you just can't get into
overhangs and other occluded areas that the trace () ray hits first.
Probably gonna be one of those things where it's only good for Bezier patches
and parametric objects. Possibly isosurfaces.
Post a reply to this message
Attachments:
Download 'surfacepropertiespattern.png' (158 KB)
Preview of image 'surfacepropertiespattern.png'
|
 |




![]()