|
 |
After a long hiatus, and extensive delays, a failing 1.5 TB drive, and 2
scrapped laptops, I reviewed enough calculus and read my collection of
differential geometry books and papers for the 50th time, so that I was able to
grasp enough of what I needed to do mathematically, to implement that in code.
It would make things easier if the nomenclature and symbols were consistent
throughout the literature, and some of the operations were better defined in the
papers themselves. Some of this was like sticking needles in my eyes.
Less than half of the struggle was the math, which turned out to not be that
difficult at all, and the more than half was descrambling all of the i's and j's
and getting the arrays laid out the right way so that the correct array elements
were getting plugged into the right places.
My analytical surface normals weren't right, but my central difference ones were
(?!) , and so I laid out all the tangents and normals and binormals of the
Frenet-Serret frames, which pointed to my curvature-related math being somehow
flipped across the diagonal with respect to my control points and Bezier
surface. Ugh.
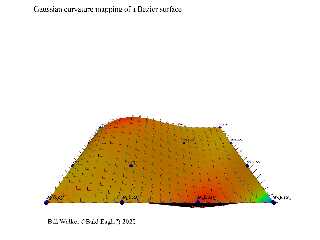
100 renders later, and I have a pretty hacky scene file that maps the Gaussian
curvature of a Bezier surface.
Never mind your p's and q's, pay detailed attention to your u's and v's!
I'm thinking that there MIGHT be a way to use some of the slope or AOI pigment
patterns to calculate the Frenet-Serret frames or any surface.... but that's
gonna require a lot more B12, coffee, and inner peace to puzzle out.
So, after a final week's struggle, here it is, a year later.
Post a reply to this message
Attachments:
Download '2022_surfacecurvatureattempt.png' (135 KB)
Preview of image '2022_surfacecurvatureattempt.png'
|
 |




![]()