"ingo" <nomail@nomail> wrote:
> The bisect of the angles in the current lines are the normals to the handles in
> that point. The handles should be equally long to get C1/G1 (?) continuity.
>
> I think, without testing,

Yes, excellent idea.

I was futzing around with something along those lines yesterday, but I'm stuck
doing it in M$ Office 365 Copilot web version - which is painful enough - but I
was working on it piecemeal, so I only had so much time in one stretch to focus.

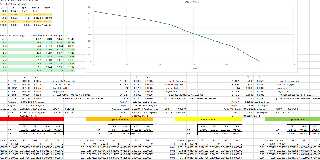
At present, I take 3 control points, bisect the angle, find the perpendicular
slope (negative reciprocal), use the equation of that line to sub in 1/3 of the
shorter vector, and solve for the control point y-values on either side of the
endpoint.

I have the Bezier splines charted using the Bernstein polynomials, and
concatenated together using "helper cells".

There are still "bumps", so I think I still need to somehow account for the
varying curvature along the splines.

Post a reply to this message

Attachments:
Download 'screenshot 2025-01-28 133147.png' (129 KB)

Preview of image 'screenshot 2025-01-28 133147.png'