|
 |
Am 16.12.2024 um 23:36 schrieb Bald Eagle:
> MichaelJF <fri### [at] t-online de> wrote:
>
> Hmmm. It looks like maybe it's a sign issue?
> Inside and outside are switched?
>
> Try just negating the function and see what happens.
>
> I'm not sure if that might have to do with the left-handed coordinate system, or
> what.
>
> - BW
>
>
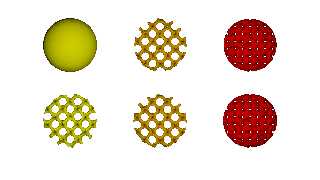
Sorry, I mixed up the image yesterday. Here is the corrected version.
It's even worse. Yesterday is was one of my tests to solve the riddle,
in which I had commented out the exponential term as a test:
#declare GyroidLatice_1 = function (x,y,z) {
select(isoCondition(x,y,z),Iso2(x,y,z),1) - //exp(isoCondition(x,y,z)/5)
}
The actual version depicts the full expression without the comment.
The difference between the functions Iso2 and Iso3 is just a change of
signs and in GyroidLatice_1 the exponential term is subtracted whereas
in GyroidLatice_2 it is added.
Below you can find the POV-part of the code with the MathMod-Code within
the comments. Maybe someone else can spot the difference. The parameter
t from MathMod is not used in this examnple.
Best regards
Michael
#declare L=23/2;
#declare c=1/10000;
#declare Th1=5/10;
#declare Th2=-8/10;
/* isoCondition=(x^N+y^N+z^N-(L-1/10)^N) (N=2)*/
#declare isoCondition = function(x,y,z) { x*x+y*y+z*z-(L-1/10)*(L-1/10) }
/* Iso =
cos(x)*sin(y)+cos(y)*sin(z)+cos(z)*sin(x) */
#declare Iso = function(x,y,z) {
cos(x)*sin(y)+cos(y)*sin(z)+cos(z)*sin(x)
}
/* DFx=((Iso(x+c,y,z,t)-Iso(x,y,z,t))/c)
DFy=((Iso(x,y+c,z,t)-Iso(x,y,z,t))/c)
DFz=((Iso(x,y,z+c,t)-Iso(x,y,z,t))/c) */
#declare DFx = function(x,y,z) { (Iso(x+c,y,z)-Iso(x,y,z))/c }
#declare DFy = function(x,y,z) { (Iso(x,y+c,z)-Iso(x,y,z))/c }
#declare DFz = function(x,y,z) { (Iso(x,y,z+c)-Iso(x,y,z))/c }
/* Rapp=(x/sqrt(x*x+y*y+z*z)) */
#declare Rapp = function(x,y,z) {x/sqrt(x*x+y*y+z*z) }
/* "Iso2 =
Iso(x+Th2*Rapp(DFx(x,y,z,t),DFy(x,y,z,t),DFz(x,y,z,t),t),
y+Th2*Rapp(DFy(x,y,z,t),DFz(x,y,z,t),DFx(x,y,z,t),t),
z+Th2*Rapp(DFz(x,y,z,t),DFx(x,y,z,t),DFy(x,y,z,t),t),t)
) */
#declare Iso2 = function(x,y,z) {
Iso(x+Th2*Rapp(DFx(x,y,z),DFy(x,y,z),DFz(x,y,z)),
y+Th2*Rapp(DFy(x,y,z),DFz(x,y,z),DFx(x,y,z)),
z+Th2*Rapp(DFz(x,y,z),DFx(x,y,z),DFy(x,y,z))
)
}
/* Iso3 =
Iso(x-Th2*Rapp(DFx(x,y,z,t),DFy(x,y,z,t),DFz(x,y,z,t),t),
y-Th2*Rapp(DFy(x,y,z,t),DFz(x,y,z,t),DFx(x,y,z,t),t),
z-Th2*Rapp(DFz(x,y,z,t),DFx(x,y,z,t),DFy(x,y,z,t),t),t)
)*/
#declare Iso3 = function(x,y,z) {
Iso(x-Th2*Rapp(DFx(x,y,z),DFy(x,y,z),DFz(x,y,z)),
y-Th2*Rapp(DFy(x,y,z),DFz(x,y,z),DFx(x,y,z)),
z-Th2*Rapp(DFz(x,y,z),DFx(x,y,z),DFy(x,y,z))
)
}
/* Iso4 =
Iso(x+Th1*Rapp(DFx(x,y,z,t),DFy(x,y,z,t),DFz(x,y,z,t),t),
y+Th1*Rapp(DFy(x,y,z,t),DFz(x,y,z,t),DFx(x,y,z,t),t),
z+Th1*Rapp(DFz(x,y,z,t),DFx(x,y,z,t),DFy(x,y,z,t),t),t)
) */
#declare Iso4 = function(x,y,z) {
Iso(x+Th1*Rapp(DFx(x,y,z),DFy(x,y,z),DFz(x,y,z)),
y+Th1*Rapp(DFy(x,y,z),DFz(x,y,z),DFx(x,y,z)),
z+Th1*Rapp(DFz(x,y,z),DFx(x,y,z),DFy(x,y,z))
)
}
/* Iso5 =
Iso(x-Th1*Rapp(DFx(x,y,z,t),DFy(x,y,z,t),DFz(x,y,z,t),t),
y-Th1*Rapp(DFy(x,y,z,t),DFz(x,y,z,t),DFx(x,y,z,t),t),
z-Th1*Rapp(DFz(x,y,z,t),DFx(x,y,z,t),DFy(x,y,z,t),t),t)
)*/
#declare Iso5 = function(x,y,z) {
Iso(x-Th1*Rapp(DFx(x,y,z),DFy(x,y,z),DFz(x,y,z)),
y-Th1*Rapp(DFy(x,y,z),DFz(x,y,z),DFx(x,y,z)),
z-Th1*Rapp(DFz(x,y,z),DFx(x,y,z),DFy(x,y,z))
)
}
/* ThickIso2=(Iso4(x,y,z,t)*Iso5(x,y,z,t)) */
#declare ThickIso2 = function(x,y,z) { Iso4(x,y,z) * Iso5(x,y,z) }
/*
GyroidLatice_1=if(isoCondition(x,y,z,t)<(0),Iso2(x,y,z,t),1)-exp(isoCondition(x,y,z,t)/5)
*/
#declare GyroidLatice_1 = function (x,y,z) {
select(isoCondition(x,y,z),Iso2(x,y,z),1) - exp(isoCondition(x,y,z)/5)
}
/*
GyroidLatice_2=if(isoCondition(x,y,z,t)<(0),Iso3(x,y,z,t),1)+exp(isoCondition(x,y,z,t)/5)
*/
#declare GyroidLatice_2 = function (x,y,z) {
select(isoCondition(x,y,z),Iso3(x,y,z),1) + exp(isoCondition(x,y,z)/5)
}
/*
GyroidLatice_3=if(isoCondition(x,y,z,t)<(0),ThickIso2(x,y,z,t),1)+exp(isoCondition(x,y,z,t)/5)
*/
#declare GyroidLatice_3 = function (x,y,z) {
select(isoCondition(x,y,z),ThickIso2(x,y,z),1) +
exp(isoCondition(x,y,z)/5)
}
#declare G1 = isosurface {
function {
GyroidLatice_1(x,y,z)
}
contained_by { sphere { 0,L-0.1} }
threshold 0
max_gradient 1000
pigment { colour Yellow }
}
#declare G2 = isosurface {
function {
GyroidLatice_2(x,y,z)
}
contained_by { sphere { 0,L-0.1 } }
threshold 0
max_gradient 1000
pigment { colour Orange }
}
#declare G3 = isosurface {
function {
GyroidLatice_3(x,y,z)
}
contained_by { sphere { 0,L-0.1 } }
threshold 0
max_gradient 1000
pigment { colour Red }
} de> wrote:
>
> Hmmm. It looks like maybe it's a sign issue?
> Inside and outside are switched?
>
> Try just negating the function and see what happens.
>
> I'm not sure if that might have to do with the left-handed coordinate system, or
> what.
>
> - BW
>
>
Sorry, I mixed up the image yesterday. Here is the corrected version.
It's even worse. Yesterday is was one of my tests to solve the riddle,
in which I had commented out the exponential term as a test:
#declare GyroidLatice_1 = function (x,y,z) {
select(isoCondition(x,y,z),Iso2(x,y,z),1) - //exp(isoCondition(x,y,z)/5)
}
The actual version depicts the full expression without the comment.
The difference between the functions Iso2 and Iso3 is just a change of
signs and in GyroidLatice_1 the exponential term is subtracted whereas
in GyroidLatice_2 it is added.
Below you can find the POV-part of the code with the MathMod-Code within
the comments. Maybe someone else can spot the difference. The parameter
t from MathMod is not used in this examnple.
Best regards
Michael
#declare L=23/2;
#declare c=1/10000;
#declare Th1=5/10;
#declare Th2=-8/10;
/* isoCondition=(x^N+y^N+z^N-(L-1/10)^N) (N=2)*/
#declare isoCondition = function(x,y,z) { x*x+y*y+z*z-(L-1/10)*(L-1/10) }
/* Iso =
cos(x)*sin(y)+cos(y)*sin(z)+cos(z)*sin(x) */
#declare Iso = function(x,y,z) {
cos(x)*sin(y)+cos(y)*sin(z)+cos(z)*sin(x)
}
/* DFx=((Iso(x+c,y,z,t)-Iso(x,y,z,t))/c)
DFy=((Iso(x,y+c,z,t)-Iso(x,y,z,t))/c)
DFz=((Iso(x,y,z+c,t)-Iso(x,y,z,t))/c) */
#declare DFx = function(x,y,z) { (Iso(x+c,y,z)-Iso(x,y,z))/c }
#declare DFy = function(x,y,z) { (Iso(x,y+c,z)-Iso(x,y,z))/c }
#declare DFz = function(x,y,z) { (Iso(x,y,z+c)-Iso(x,y,z))/c }
/* Rapp=(x/sqrt(x*x+y*y+z*z)) */
#declare Rapp = function(x,y,z) {x/sqrt(x*x+y*y+z*z) }
/* "Iso2 =
Iso(x+Th2*Rapp(DFx(x,y,z,t),DFy(x,y,z,t),DFz(x,y,z,t),t),
y+Th2*Rapp(DFy(x,y,z,t),DFz(x,y,z,t),DFx(x,y,z,t),t),
z+Th2*Rapp(DFz(x,y,z,t),DFx(x,y,z,t),DFy(x,y,z,t),t),t)
) */
#declare Iso2 = function(x,y,z) {
Iso(x+Th2*Rapp(DFx(x,y,z),DFy(x,y,z),DFz(x,y,z)),
y+Th2*Rapp(DFy(x,y,z),DFz(x,y,z),DFx(x,y,z)),
z+Th2*Rapp(DFz(x,y,z),DFx(x,y,z),DFy(x,y,z))
)
}
/* Iso3 =
Iso(x-Th2*Rapp(DFx(x,y,z,t),DFy(x,y,z,t),DFz(x,y,z,t),t),
y-Th2*Rapp(DFy(x,y,z,t),DFz(x,y,z,t),DFx(x,y,z,t),t),
z-Th2*Rapp(DFz(x,y,z,t),DFx(x,y,z,t),DFy(x,y,z,t),t),t)
)*/
#declare Iso3 = function(x,y,z) {
Iso(x-Th2*Rapp(DFx(x,y,z),DFy(x,y,z),DFz(x,y,z)),
y-Th2*Rapp(DFy(x,y,z),DFz(x,y,z),DFx(x,y,z)),
z-Th2*Rapp(DFz(x,y,z),DFx(x,y,z),DFy(x,y,z))
)
}
/* Iso4 =
Iso(x+Th1*Rapp(DFx(x,y,z,t),DFy(x,y,z,t),DFz(x,y,z,t),t),
y+Th1*Rapp(DFy(x,y,z,t),DFz(x,y,z,t),DFx(x,y,z,t),t),
z+Th1*Rapp(DFz(x,y,z,t),DFx(x,y,z,t),DFy(x,y,z,t),t),t)
) */
#declare Iso4 = function(x,y,z) {
Iso(x+Th1*Rapp(DFx(x,y,z),DFy(x,y,z),DFz(x,y,z)),
y+Th1*Rapp(DFy(x,y,z),DFz(x,y,z),DFx(x,y,z)),
z+Th1*Rapp(DFz(x,y,z),DFx(x,y,z),DFy(x,y,z))
)
}
/* Iso5 =
Iso(x-Th1*Rapp(DFx(x,y,z,t),DFy(x,y,z,t),DFz(x,y,z,t),t),
y-Th1*Rapp(DFy(x,y,z,t),DFz(x,y,z,t),DFx(x,y,z,t),t),
z-Th1*Rapp(DFz(x,y,z,t),DFx(x,y,z,t),DFy(x,y,z,t),t),t)
)*/
#declare Iso5 = function(x,y,z) {
Iso(x-Th1*Rapp(DFx(x,y,z),DFy(x,y,z),DFz(x,y,z)),
y-Th1*Rapp(DFy(x,y,z),DFz(x,y,z),DFx(x,y,z)),
z-Th1*Rapp(DFz(x,y,z),DFx(x,y,z),DFy(x,y,z))
)
}
/* ThickIso2=(Iso4(x,y,z,t)*Iso5(x,y,z,t)) */
#declare ThickIso2 = function(x,y,z) { Iso4(x,y,z) * Iso5(x,y,z) }
/*
GyroidLatice_1=if(isoCondition(x,y,z,t)<(0),Iso2(x,y,z,t),1)-exp(isoCondition(x,y,z,t)/5)
*/
#declare GyroidLatice_1 = function (x,y,z) {
select(isoCondition(x,y,z),Iso2(x,y,z),1) - exp(isoCondition(x,y,z)/5)
}
/*
GyroidLatice_2=if(isoCondition(x,y,z,t)<(0),Iso3(x,y,z,t),1)+exp(isoCondition(x,y,z,t)/5)
*/
#declare GyroidLatice_2 = function (x,y,z) {
select(isoCondition(x,y,z),Iso3(x,y,z),1) + exp(isoCondition(x,y,z)/5)
}
/*
GyroidLatice_3=if(isoCondition(x,y,z,t)<(0),ThickIso2(x,y,z,t),1)+exp(isoCondition(x,y,z,t)/5)
*/
#declare GyroidLatice_3 = function (x,y,z) {
select(isoCondition(x,y,z),ThickIso2(x,y,z),1) +
exp(isoCondition(x,y,z)/5)
}
#declare G1 = isosurface {
function {
GyroidLatice_1(x,y,z)
}
contained_by { sphere { 0,L-0.1} }
threshold 0
max_gradient 1000
pigment { colour Yellow }
}
#declare G2 = isosurface {
function {
GyroidLatice_2(x,y,z)
}
contained_by { sphere { 0,L-0.1 } }
threshold 0
max_gradient 1000
pigment { colour Orange }
}
#declare G3 = isosurface {
function {
GyroidLatice_3(x,y,z)
}
contained_by { sphere { 0,L-0.1 } }
threshold 0
max_gradient 1000
pigment { colour Red }
}
Post a reply to this message
Attachments:
Download 'zeige_ball01.png' (413 KB)
Preview of image 'zeige_ball01.png'
|
 |




![]()