 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
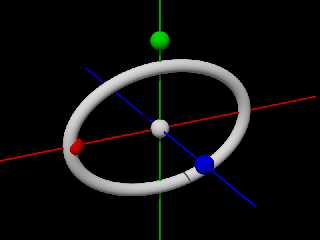
Hopefully this is to spec.
The green circles are torus{} objects to show that the cross section is indeed
exactly circular.
Not my best work, and it's only a parametric, not an implicit equation, but
perhaps I can "implicitize" it.
It was the z part that needed some figuring.
Hope you like. :)
Post a reply to this message
Attachments:
Download 'ellipticaltorus.png' (58 KB)
Preview of image 'ellipticaltorus.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 5/2/20 9:27 AM, Bald Eagle wrote:
> Hopefully this is to spec.
>
> The green circles are torus{} objects to show that the cross section is indeed
> exactly circular.
>
> Not my best work, and it's only a parametric, not an implicit equation, but
> perhaps I can "implicitize" it.
>
> It was the z part that needed some figuring.
>
> Hope you like. :)
>
It is a cool shape.
I couldn't resist trying it though I have almost no experience with
parametric surfaces... First thing I learned is the parametric max
gradient doesn't seem to be much related to the isosurface one by value
at least...
Using:
parametric {
function { (_a + _R * cos(u)) * _r * cos(v) }
function { (_b + _R * cos(u)) * _r * sin(v) }
function { _R * _r * sin(u) }
<0,-pi>, <2*pi,pi>
contained_by { sphere{0, 1.5} }
max_gradient 0.005
accuracy 0.0005
precompute 10 x,y,z
pigment {rgb 1}
}
I started with max_gradient 1.0 as I might an isosurface, but ended up
as above.
// povr2 Parametric_EllipticalTorus.pov +p +w800 +h600 +a0.3 +am2 +r3
// 21,348,576,112 maxg 1.000, accuracy 0.0001. 3058.277s
// 5,309,618,895 maxg 0.500, accuracy 0.0005. 754.430s
// 1,164,854,065 maxg 0.100, accuracy 0.0005. 165.657s
// 744,145,888 maxg 0.025, accuracy 0.0005. 106.139s
// 683,049,468 maxg 0.005, accuracy 0.0005. 97.377s (24.7s)
25s elapsed pretty slow but much faster than most any parametric I have
ever gotten from anyone and just run. What were you using for settings
and seeing for run times?
Aside: My f_eblob() function often ends up with max gradients well below
1.0 too. There I know I'm doing some stuff that takes out some of the
exponential behavior. It makes the gradient small but more linear.
Bill P.
Post a reply to this message
Attachments:
Download 'parametric_ellipticaltorus.png' (50 KB)
Preview of image 'parametric_ellipticaltorus.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> It is a cool shape.
Yes, and relatively simple, so I was surprised there wasn't a lot more out there
about it, and that I hadn't come across it in my broad and extensive reading
about Dupin cylcides, Clifford tori, geometric inversion, embedding in 3-space,
Villarceau circles, etc.
> "I couldn't resist trying it..."
lol - well of course not. :D
> What were you using for settings and seeing for run times?
I have some actual parametric code in the scene that stays commented out, so I
didn't use that. I use Paul Nylander's method of calculating stepwise points
on a grid of the function and fill in those quadrilaterals with 2 triangles.
This was run in steps of Theta/240 and phi/60
I suppose I ought to calculate some vertex normals and upgrade the code to use
smooth_triangles. And the face normals seemed to be inverted from what I
expected - so it totally needs work. But I can mark all the vertices and draw
the grid just by setting the flags to run those code blocks.
And it's - FAST. :)
Parser Statistics
----------------------------------------------------------------------------
Finite Objects: 86557
Infinite Objects: 0
Light Sources: 1
Total: 86558
----------------------------------------------------------------------------
Parser Time
Parse Time: 0 hours 0 minutes 1 seconds (1.639 seconds)
using 1 thread(s)
Bounding Time: 0 hours 0 minutes 0 seconds (0.163 seconds)
using 1 thread(s)
----------------------------------------------------------------------------
Render Options
Quality: 9
Bounding boxes.......On Bounding threshold: 3
Antialiasing.........On (Method 1, Threshold 0.300, Depth 3, Jitter 1.00,
Gamma 2.50)
----------------------------------------------------------------------------
Render Statistics
Image Resolution 640 x 480
----------------------------------------------------------------------------
Pixels: 326400 Samples: 128421 Smpls/Pxl: 0.39
Rays: 508059 Saved: 6812 Max Level: 2/5
----------------------------------------------------------------------------
Ray->Shape Intersection Tests Succeeded Percentage
----------------------------------------------------------------------------
Cone/Cylinder 9987 4897 49.03
Torus 83998 29868 35.56
Torus Bound 83998 33072 39.37
Triangle 1160673 84193 7.25
True Type Font 86841 42100 48.48
Bounding Box 18792623 5987477 31.86
----------------------------------------------------------------------------
Roots tested: 33072 eliminated: 13868
Shadow Ray Tests: 118517 Succeeded: 15672
Shadow Cache Hits: 5572
Reflected Rays: 53238
----------------------------------------------------------------------------
----------------------------------------------------------------------------
Render Time:
Photon Time: No photons
Radiosity Time: No radiosity
Trace Time: 0 hours 0 minutes 0 seconds (0.682 seconds)
using 4 thread(s) with 0.-04 CPU-seconds total
POV-Ray finished org> wrote:
> It is a cool shape.
Yes, and relatively simple, so I was surprised there wasn't a lot more out there
about it, and that I hadn't come across it in my broad and extensive reading
about Dupin cylcides, Clifford tori, geometric inversion, embedding in 3-space,
Villarceau circles, etc.
> "I couldn't resist trying it..."
lol - well of course not. :D
> What were you using for settings and seeing for run times?
I have some actual parametric code in the scene that stays commented out, so I
didn't use that. I use Paul Nylander's method of calculating stepwise points
on a grid of the function and fill in those quadrilaterals with 2 triangles.
This was run in steps of Theta/240 and phi/60
I suppose I ought to calculate some vertex normals and upgrade the code to use
smooth_triangles. And the face normals seemed to be inverted from what I
expected - so it totally needs work. But I can mark all the vertices and draw
the grid just by setting the flags to run those code blocks.
And it's - FAST. :)
Parser Statistics
----------------------------------------------------------------------------
Finite Objects: 86557
Infinite Objects: 0
Light Sources: 1
Total: 86558
----------------------------------------------------------------------------
Parser Time
Parse Time: 0 hours 0 minutes 1 seconds (1.639 seconds)
using 1 thread(s)
Bounding Time: 0 hours 0 minutes 0 seconds (0.163 seconds)
using 1 thread(s)
----------------------------------------------------------------------------
Render Options
Quality: 9
Bounding boxes.......On Bounding threshold: 3
Antialiasing.........On (Method 1, Threshold 0.300, Depth 3, Jitter 1.00,
Gamma 2.50)
----------------------------------------------------------------------------
Render Statistics
Image Resolution 640 x 480
----------------------------------------------------------------------------
Pixels: 326400 Samples: 128421 Smpls/Pxl: 0.39
Rays: 508059 Saved: 6812 Max Level: 2/5
----------------------------------------------------------------------------
Ray->Shape Intersection Tests Succeeded Percentage
----------------------------------------------------------------------------
Cone/Cylinder 9987 4897 49.03
Torus 83998 29868 35.56
Torus Bound 83998 33072 39.37
Triangle 1160673 84193 7.25
True Type Font 86841 42100 48.48
Bounding Box 18792623 5987477 31.86
----------------------------------------------------------------------------
Roots tested: 33072 eliminated: 13868
Shadow Ray Tests: 118517 Succeeded: 15672
Shadow Cache Hits: 5572
Reflected Rays: 53238
----------------------------------------------------------------------------
----------------------------------------------------------------------------
Render Time:
Photon Time: No photons
Radiosity Time: No radiosity
Trace Time: 0 hours 0 minutes 0 seconds (0.682 seconds)
using 4 thread(s) with 0.-04 CPU-seconds total
POV-Ray finished
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> > "I couldn't resist trying it..."
>
> lol - well of course not. :D
And I couldn't resist implicitizing it.
I mussssst ... do..... the math..... yesss....
my Precious........!
And here is The One Elliptical Ring.
The gradient is only about 4.5 :)
However, you will notice that it doesn't render correctly when axis-aligned.
If I rotate it by 1 degree (0.5 isn't enough), then it becomes fully visible.
Do we smell a root-finding problem? Ugh.
Martijn does some interesting little tweaks that I haven't thought out
completely to fix holes and other artifacts:
https://www.youtube.com/watch?v=-adHIyjIYgk (14 min mark)
No idea if any of that is related to POV-Ray isosurface issues.
I think he might address some similar issues either earlier or in Part 2.
Anyway, I'm off to bed, but had to post this for Ricky.
Maybe tomorrow I will be able to better parameterize it.
Boo-Ya! net> wrote:
> > "I couldn't resist trying it..."
>
> lol - well of course not. :D
And I couldn't resist implicitizing it.
I mussssst ... do..... the math..... yesss....
my Precious........!
And here is The One Elliptical Ring.
The gradient is only about 4.5 :)
However, you will notice that it doesn't render correctly when axis-aligned.
If I rotate it by 1 degree (0.5 isn't enough), then it becomes fully visible.
Do we smell a root-finding problem? Ugh.
Martijn does some interesting little tweaks that I haven't thought out
completely to fix holes and other artifacts:
https://www.youtube.com/watch?v=-adHIyjIYgk (14 min mark)
No idea if any of that is related to POV-Ray isosurface issues.
I think he might address some similar issues either earlier or in Part 2.
Anyway, I'm off to bed, but had to post this for Ricky.
Maybe tomorrow I will be able to better parameterize it.
Boo-Ya!
Post a reply to this message
Attachments:
Download 'implicitellipticaltorus.png' (49 KB)
Preview of image 'implicitellipticaltorus.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 5/3/20 12:04 AM, Bald Eagle wrote:
> "Bald Eagle" <cre### [at] netscape net> wrote:
>
>>> "I couldn't resist trying it..."
>>
>> lol - well of course not. :D
>
> And I couldn't resist implicitizing it.
> I mussssst ... do..... the math..... yesss....
> my Precious........!
>
> And here is The One Elliptical Ring.
> The gradient is only about 4.5 :)
>
> However, you will notice that it doesn't render correctly when axis-aligned.
> If I rotate it by 1 degree (0.5 isn't enough), then it becomes fully visible.
>
> Do we smell a root-finding problem? Ugh.
>
> Martijn does some interesting little tweaks that I haven't thought out
> completely to fix holes and other artifacts:
> https://www.youtube.com/watch?v=-adHIyjIYgk (14 min mark)
> No idea if any of that is related to POV-Ray isosurface issues.
> I think he might address some similar issues either earlier or in Part 2.
>
> Anyway, I'm off to bed, but had to post this for Ricky.
>
> Maybe tomorrow I will be able to better parameterize it.
>
> Boo-Ya!
>
:-) Thanks for pushing here. Does this all work only when the major axis
is 1.0 or something?
I grabbed what you did and tried it after a little re-work to align it
with the f_torus behavior and on testing the constant sphere width was
not maintained when a != b - or when I changed the major axis to other
than one. The last was relatively easy to fix. I had no luck with a!=b
across all testing - though I could get some subsets of parameters to work.
Might be I screwed something up in reworking it. Will come back to it
later, but if there are assumptions with the implicit form use,it would
be helpful to know.
Bill P. net> wrote:
>
>>> "I couldn't resist trying it..."
>>
>> lol - well of course not. :D
>
> And I couldn't resist implicitizing it.
> I mussssst ... do..... the math..... yesss....
> my Precious........!
>
> And here is The One Elliptical Ring.
> The gradient is only about 4.5 :)
>
> However, you will notice that it doesn't render correctly when axis-aligned.
> If I rotate it by 1 degree (0.5 isn't enough), then it becomes fully visible.
>
> Do we smell a root-finding problem? Ugh.
>
> Martijn does some interesting little tweaks that I haven't thought out
> completely to fix holes and other artifacts:
> https://www.youtube.com/watch?v=-adHIyjIYgk (14 min mark)
> No idea if any of that is related to POV-Ray isosurface issues.
> I think he might address some similar issues either earlier or in Part 2.
>
> Anyway, I'm off to bed, but had to post this for Ricky.
>
> Maybe tomorrow I will be able to better parameterize it.
>
> Boo-Ya!
>
:-) Thanks for pushing here. Does this all work only when the major axis
is 1.0 or something?
I grabbed what you did and tried it after a little re-work to align it
with the f_torus behavior and on testing the constant sphere width was
not maintained when a != b - or when I changed the major axis to other
than one. The last was relatively easy to fix. I had no luck with a!=b
across all testing - though I could get some subsets of parameters to work.
Might be I screwed something up in reworking it. Will come back to it
later, but if there are assumptions with the implicit form use,it would
be helpful to know.
Bill P.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> :-) Thanks for pushing here. Does this all work only when the major axis
> is 1.0 or something?
Unfortunately, I thought, nay - believed (at 1am) that I had gotten it
sufficiently worked out so that I could just get it prettied up and all would be
fine, but of course it has proven to be a bit more challenging than that.
I have been trying to get it re-worked out myself, but how exactly the
z-parameter gets adjusted to compensate for the x and y stretching in the
implicit form is unclear.
I too have been trying to get it to be consistent with POV-Ray's torus in the
xz-plane - I just need to hit upon the proper form.
On the plus side, after a few dozen experiments, I have at least one function
that's sufficiently interesting to pursue at some other point.
It's maddening to be this tantalizingly close and still not _have_ it. org> wrote:
> :-) Thanks for pushing here. Does this all work only when the major axis
> is 1.0 or something?
Unfortunately, I thought, nay - believed (at 1am) that I had gotten it
sufficiently worked out so that I could just get it prettied up and all would be
fine, but of course it has proven to be a bit more challenging than that.
I have been trying to get it re-worked out myself, but how exactly the
z-parameter gets adjusted to compensate for the x and y stretching in the
implicit form is unclear.
I too have been trying to get it to be consistent with POV-Ray's torus in the
xz-plane - I just need to hit upon the proper form.
On the plus side, after a few dozen experiments, I have at least one function
that's sufficiently interesting to pursue at some other point.
It's maddening to be this tantalizingly close and still not _have_ it.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
So - working with a circle and an ellipse to begin working out the particulars,
it's apparent that the inside and outside curves in the xz plane are going to be
offset curves. (and so they rear their heads _again_!)
I don't know if those curves are themselves ellipses or not.
And that may factor into how difficult it is to derive an equation for the
desired surface.
I feel some 3D diagrams coming...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
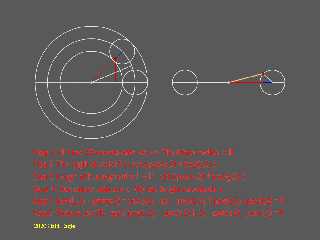
First diagram shows plan and elevation of a torus.
The goal is to next adapt everything in Step 2 to an ellipse instead of a
circle.
I think I have it worked out, but I get no visible isosurface, so the math and
logic need to be checked, then I can go isosurface idiosyncrasy hunting.
Post a reply to this message
Attachments:
Download 'implicitellipticaltorus.png' (124 KB)
Preview of image 'implicitellipticaltorus.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 5/3/20 4:30 PM, Bald Eagle wrote:
> William F Pokorny <ano### [at] anonymous org> wrote:
>
>> :-) Thanks for pushing here. Does this all work only when the major axis
>> is 1.0 or something?
>
> Unfortunately, I thought, nay - believed (at 1am) that I had gotten it
> sufficiently worked out so that I could just get it prettied up and all would be
> fine, but of course it has proven to be a bit more challenging than that.
> I have been trying to get it re-worked out myself, but how exactly the
> z-parameter gets adjusted to compensate for the x and y stretching in the
> implicit form is unclear.
>
> I too have been trying to get it to be consistent with POV-Ray's torus in the
> xz-plane - I just need to hit upon the proper form.
>
> On the plus side, after a few dozen experiments, I have at least one function
> that's sufficiently interesting to pursue at some other point.
>
> It's maddening to be this tantalizingly close and still not _have_ it.
>
FYI. I've not recently looked at it, but back in 2006 Bruno Cabasson
worked up some code for elliptical tori implemented with sphere_sweeps
and blobs. Perhaps useful to review that work as we look for an
f_elliptical_torus() or complete parametric solution.
Given we can use blobs as potential patterns in functions/isosurfaces in
v38, perhaps this a path to something practical for Cousin Ricky?
The sphere_sweep as a general solution is not very attractive in v37 and
prior due bugs. Situations is better in v38 - and still better in povr
but the sphere_sweep probably not the fastest.
With both approaches expect tolerances to any math ideal, but perhaps we
are stuck with a fuzzy result in any case?
I captured his code in my sphere_sweep test cases, let me see if small
enough to just attach it - yep. Warning! Some chance I hacked on the
scene file a little from what was originally posted - I didn't check.
Bill P. org> wrote:
>
>> :-) Thanks for pushing here. Does this all work only when the major axis
>> is 1.0 or something?
>
> Unfortunately, I thought, nay - believed (at 1am) that I had gotten it
> sufficiently worked out so that I could just get it prettied up and all would be
> fine, but of course it has proven to be a bit more challenging than that.
> I have been trying to get it re-worked out myself, but how exactly the
> z-parameter gets adjusted to compensate for the x and y stretching in the
> implicit form is unclear.
>
> I too have been trying to get it to be consistent with POV-Ray's torus in the
> xz-plane - I just need to hit upon the proper form.
>
> On the plus side, after a few dozen experiments, I have at least one function
> that's sufficiently interesting to pursue at some other point.
>
> It's maddening to be this tantalizingly close and still not _have_ it.
>
FYI. I've not recently looked at it, but back in 2006 Bruno Cabasson
worked up some code for elliptical tori implemented with sphere_sweeps
and blobs. Perhaps useful to review that work as we look for an
f_elliptical_torus() or complete parametric solution.
Given we can use blobs as potential patterns in functions/isosurfaces in
v38, perhaps this a path to something practical for Cousin Ricky?
The sphere_sweep as a general solution is not very attractive in v37 and
prior due bugs. Situations is better in v38 - and still better in povr
but the sphere_sweep probably not the fastest.
With both approaches expect tolerances to any math ideal, but perhaps we
are stuck with a fuzzy result in any case?
I captured his code in my sphere_sweep test cases, let me see if small
enough to just attach it - yep. Warning! Some chance I hacked on the
scene file a little from what was originally posted - I didn't check.
Bill P.
Post a reply to this message
Attachments:
Download 'utf-8' (6 KB)
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
Perhaps useful to review that work as we look for an
> f_elliptical_torus() or complete parametric solution.
I'll go back to my initial post and see what else I need for the parametric.
I had a key insight last night that I need to pursue when I get back later.
With regard to a workaround, if needed:
http://www.econym.demon.co.uk/isotut/splines.htm
Which I should have thought of much much earlier. org> wrote:
Perhaps useful to review that work as we look for an
> f_elliptical_torus() or complete parametric solution.
I'll go back to my initial post and see what else I need for the parametric.
I had a key insight last night that I need to pursue when I get back later.
With regard to a workaround, if needed:
http://www.econym.demon.co.uk/isotut/splines.htm
Which I should have thought of much much earlier.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()