 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Everyone is familiar with the roundcone, a convex object, and the sphere sweep
derived from it. A while ago I thought about connecting three spheres smoothly
with cones. When you join two roundcones, there are a pair of points where the
normals to the sphere and the two cones are identical.
Adding a pair of smooth triangles with vertices at these points gives a "solid"
object. This doesn't have C_1 since the line joining one normal point
to another usually penetrates the cone. However, the interpolation of the normal
on the smooth triangle is not a terrible match for the normal on the curve of
the intersection of the smooth triangle and the cone. The discontinuity appears
no more prominent than the false discontinuity observed when there is a
curvature discontinuity.
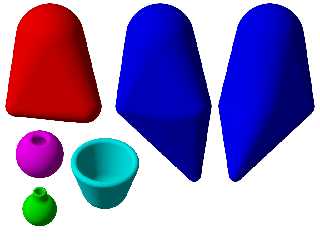
The image gives a fat triangle, a fat quadrilateral, some spheres with smooth
holes and a hollow roundcone (surprisingly tricky).
The fat quadrilateral is best not done with a pair of fat triangles - a
prominent crease is almost unavoidable on one side for non trivial
quadrilaterals. This one uses four fat triangles with a central sphere. The
default is to use the average of the four vertex spheres, but I've had to
multiply that by 1.5 to minimise any creases.
I've not seen such objects used, though it's hard to believe I've produced these
for the first time.
The next step is to produce Bezier patches using fat triangles. See the next
post in this thread
Post a reply to this message
Attachments:
Download 'fat_bezier_basic_examples.png' (101 KB)
Preview of image 'fat_bezier_basic_examples.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
The image gives some test examples that use fat Bezier patches, made up of fat
strips. fat fans, fat triangles or fat quadrilaterals.
The arrowhead is a single fat Bezier triangular patch (with its reflection) with
a hollow cylinder attached to one of the vertices. The Starck Juicer was the
subject of a recent set of posts. The body is mainly sphere sweeps (of a single
Bezier segment variety - I like the control) The legs are two fat strips.
I like the knife, which needs two fat fans, three fat strips - one specifically
the transition region.
The glasses are produced with a glass making #macro, using the sphere blends and
hollow roundcone.
The #macros in use do need e.g. eight vectors and eight radii for a strip, ten
for a triangular patch and sixteen for a quadrilateral patch. Challenging, but
not impossible for an object using very few patches - the seat and back of the
chair are each made of a single quadrilateral patch.
For static objects, there may be no advantage (and a disadvantage of needing
good 3D visualisation to input the co-ordinates and radii) over a modeller.
However, it is possible to parameterise some of the co-ordinates or radii to
simply change a shape, as in the next post to this thread.
Post a reply to this message
Attachments:
Download 'fat_bezier_test_examples.png' (193 KB)
Preview of image 'fat_bezier_test_examples.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
The wings are made of two quadrilateral patches and a triangular patch. One
quadrilateral patch blends to the fuselage, the second forms the main wing. The
triangular patch forms the wingtip.
Changing a single parameter allows for the wing to curve upwards when providing
lift.
The tail is a single fat triangular patch with a hollow roundcone for the intake
differenced for the exhaust. Any differences have to be done as locally with
the patch definition as possible - the numbers of objects in a patch mean a
difference with a union of many patches with take forever to render.
Lucky clipka is working on parse. Parse time was 31 seconds, render time 8
seconds at 1024x768.
I've posted these to see if there is enough interest for me to either post code,
bugs and all, or spend (quite a bit of) time cleaning it up and uploading to
objects.
I've tried to see if a human figure is possible. It sort of is, but parametric
posing is difficult, and I must be doing the clothing wrong, since that has been
very difficult. I will go back to see how POVPerson did it.
Post a reply to this message
Attachments:
Download 'fat_bezier_reaper.png' (108 KB)
Preview of image 'fat_bezier_reaper.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
"JimT" <nomail@nomail> wrote:
looks all very impressive, I really like the office chair.
> I've posted these to see if there is enough interest for me to either post code,
> bugs and all, or spend (quite a bit of) time cleaning it up and uploading to
> objects.
I'd love to see the code for the shapes of your first post, hope you can post.
regards, jr.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 29.05.2018 um 16:14 schrieb JimT:
> Everyone is familiar with the roundcone, a convex object, and the sphere sweep
> derived from it.
Is everyone?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 29/05/2018 20:06, clipka wrote:
> Am 29.05.2018 um 16:14 schrieb JimT:
>> Everyone is familiar with the roundcone, a convex object, and the sphere sweep
>> derived from it.
>
> Is everyone?
>
Not me, for one.
--
Regards
Stephen
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 18-05-29 à 15:06, clipka a écrit :
> Am 29.05.2018 um 16:14 schrieb JimT:
>> Everyone is familiar with the roundcone, a convex object, and the sphere sweep
>> derived from it.
>
> Is everyone?
>
I do know about the tree versions, but don't remember using them.
Two with spherical ends and one with flat caps with a rounded connection
with the side.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> I've posted these to see if there is enough interest for me to either post code,
> bugs and all, or spend (quite a bit of) time cleaning it up and uploading to
> objects.
>
Thanks Jim, this is an interesting idea.
I made some trials on the same idea although my computations were the other way
round : from the three spheres, let say in the horizontal plane, I first
computed the 2 tangent planes to the three spheres, the one above the spheres
and the one below. From the 6 tangency points, we get 6 lines. Grouping these
lines by pair, we get 3 cones. More specifically, in the middlee of each pair is
a line through the centers of 2 spheres, and the corresponding lathe object
around the middle line is the cone to be added.
This construction shows if I am not wrong that the cone is tangent to the plane,
so I did not understand your C1-problems in your first message.
My goal was much more simple than what you did. I just wanted to draw rounded
boxes with different radius along the edges.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"lelama" <nomail@nomail> wrote:
> > I've posted these to see if there is enough interest for me to either post code,
> > bugs and all, or spend (quite a bit of) time cleaning it up and uploading to
> > objects.
> >
>
> Thanks Jim, this is an interesting idea.
>
> I made some trials on the same idea although my computations were the other way
> round : from the three spheres, let say in the horizontal plane, I first
> computed the 2 tangent planes to the three spheres, the one above the spheres
> and the one below.
I accept your argument. Three spheres will have a pair of tangent planes and if
you join two of the tangent points, you have a line with two identical normals
at the ends which must be a generator of the tangent cone. The fat triangle
therefore has to be C_1 and the apparent discontinuity is all to do with
discontinuity of curvature.
Coming from the tangent cones direction, I didn't see why the two tangent points
had to be on a single generator of the tangent cone and assumed they weren't.
Checking in an actual example:
Nor21 = <-0.59960801,-0.05058799,0.79869336>
Nor22 = <-0.59960801,-0.05058799,0.79869336>
Nor23 = <-0.59960801,-0.05058799,0.79869336>
that is, three identical normals to 8 dp. So, thanks, I now realise the smooth
triangles are not needed - ordinary triangles or a pair of transformed prism
objects will do (a prism would help with CSG intersections and differences).
Simplifying the construction of a single fat triangle should have an effect on
the speed of parsing - which would be a help since it is slooow.
>From the 6 tangency points, we get 6 lines. Grouping these
> lines by pair, we get 3 cones. More specifically, in the middlee of each pair is
> a line through the centers of 2 spheres, and the corresponding lathe object
> around the middle line is the cone to be added.
>
> This construction shows if I am not wrong that the cone is tangent to the plane,
> so I did not understand your C1-problems in your first message.
>
> My goal was much more simple than what you did. I just wanted to draw rounded
> boxes with different radius along the edges.
I've added an image with the triangles in a different colour. I initially
expected the edges to be subtly curved, which they are not. Printing out the
three normals is a confirmations.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
clipka <ano### [at] anonymous org> wrote:
> Am 29.05.2018 um 16:14 schrieb JimT:
> > Everyone is familiar with the roundcone, a convex object, and the sphere sweep
> > derived from it.
>
> Is everyone?
Round_Cone, Round_Cone_Union, Round_Cone_Merge and Round_Cone2 and Round_Cone3
variants are in shapes.inc from John vanSickle.
Not that I am familiar with everything in the include files. I constructed a
round cone #macro before I was informed about the shapes.inc version. I wanted
it to use in a single Bezier segment version of a sphere sweep that would cope
with the sphere radius going negative by coming to a point, being absent while
the radius was negative, and then starting up again from a point.
I guess most people are familiar with the sphere sweep.
Anyway, thanks to isama, I am now happy to assert the fat triangle is C_1, and
go away to simplify the code. org> wrote:
> Am 29.05.2018 um 16:14 schrieb JimT:
> > Everyone is familiar with the roundcone, a convex object, and the sphere sweep
> > derived from it.
>
> Is everyone?
Round_Cone, Round_Cone_Union, Round_Cone_Merge and Round_Cone2 and Round_Cone3
variants are in shapes.inc from John vanSickle.
Not that I am familiar with everything in the include files. I constructed a
round cone #macro before I was informed about the shapes.inc version. I wanted
it to use in a single Bezier segment version of a sphere sweep that would cope
with the sphere radius going negative by coming to a point, being absent while
the radius was negative, and then starting up again from a point.
I guess most people are familiar with the sphere sweep.
Anyway, thanks to isama, I am now happy to assert the fat triangle is C_1, and
go away to simplify the code.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()