 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I didn't have as much time as I would have liked to explore this,
but after fiddling with the Dupin cyclide in both isosurface (implicit) and
parametric form, I found the parameters to be highly unintuitive, the desired
shape very difficult to achieve and control, and the constraints on the
parameters too complex to be easily implemented.
I hadn't gotten around to unraveling the implicit equation to fit the syntax for
a polynomial.
So I home-cooked a formula for the minor radius of a torus, and patched that
into the code I had for a normal parametric torus, and it gives me the desired
shape with only 3 values required.
It is, however, SLLLLllllllllllooooooooooowwwwwwww.
Which is to be expected for a parametric, but probably with Ingo's slick method,
it will be fast enough to do what I want.
See how the toroid (left) has a variable minor radius, and when rotated around
the x axis appears to be equally wide along both front and back.
The radii, position, and camera placement were all chosen to get that to work
out.
Further work ought to yield a torus with a user-supplied major radius, which
when placed at any distance from the camera will automatically calculate the
proper radii for the fore and aft sections so as to be _just_ visible (1 pixel
wide or high)
// Dupin cylide and Faux-Dupin-cyclide object
// Bald Eagle 2017-05
#version 3.7;
global_settings {
assumed_gamma 1.0
}
#include "colors.inc"
#declare Location = <0, 0, -10>;
#declare LookAt = <0, 0, 0>;
camera {
location Location
right x*image_width/image_height
look_at LookAt
}
sky_sphere {pigment {White*0}}
light_source {<0, 10, -50> color White}
#declare Method = 2;
#switch (Method)
#case (0)
// Dupin Cyclide with isosurface
#declare a = 3;
#declare b = 1;
#declare c = sqrt (a*a - b*b);
#debug concat ( " c = ", str (c, 3, 3), "\n")
#declare d = 2;
// c < d < a
isosurface {
function {pow(x*x + y*y + z*z + b*b - d*d, 2) - 4*pow(a*x - c*d, 2) -
4*(b*b*y*y)}
threshold 0
accuracy 0.0001
max_gradient 3000
contained_by {box {<-10, -10, -10>, <10, 10, 10>}}
texture {
pigment {color rgb <0.3, 1.0, 0.1>}
finish {phong 1}
}
} // end isosurface
#break
#case (1)
// Dupin Cyclide with parametric
#declare a = 4;
#declare b = 1;
#declare c = sqrt (a*a - b*b);
#debug concat ( " c = ", str (c, 3, 3), "\n")
#declare d = 3.9;
// c < d < a
parametric {
function { ( d*(c-a*cos(u)*cos(v)) + (b*b*cos(u)) ) / ( a-c*cos(u)*cos(v) ) },
// x-axis
function { ( b*sin(u)*(a-d*cos(v)) ) / ( a-c*cos(u)*cos(v) ) }, // y-axis
function { ( (b*sin(v))*(c*cos(u)-d) ) / (a-c*cos(u)*cos(v)) } //
z-axis
<0, 0>, <2*pi, 2*pi>
//contained_by { sphere { 0,1 } } // texturing problem, use box instead to see!
contained_by { box { <-20, -10, -10>, <10, 10, 10> } }
// max_gradient 2
accuracy 0.005 // 0.001 default, lower slower but better
precompute 15 x,y,z // precompute [x,y,z] normally gives faster rendering
(<=20)
//rotate 180*x
scale 1
texture {pigment {color rgb <1, 0, 0> } }
} // end parametric
#break
#case (2)
// Home cooked variable torus with parametric
// Normal Torus
// #declare X = function (T, P, R, r) { cos(T) * ( R + r*cos(P) ) }
// #declare Y = function (T, P, R, r) { sin(T) * ( R + r*cos(P) ) }
// #declare Z = function (P, r) { r*sin(P) }
// So, the idea is that the minor radius circle that gets swept around the major
radius cirlce to form the torus varies from one radius to the other and then
back
// the average of the radii is (r1 + r2)/2, and then to get the large radius, we
add (r1 - r2)/2 and to get the smalll radius, we subtract (r1 - r2)/2
// as u varies, cosine u goes from 1 to 0, and then to -1 and back to 0 and then
1
// multiplying cosine u by (r1 - r2)/2 and adding to the average gives us a
varying minor radius - Max to average, and then average to min radius, and then
back to avg and max
// camera is at z = -10
// left variable torus shows varying minor radius
// major radius is 5
// when tilted back, and translated back 5 units, front of torus is at 0, rear
of torus is at -10, or absolute distances of 10 and 20 (double)
// far radius is double that of near radius, but when viewed at an extreme tilt,
they both have the same apparent width
#macro vtorus (Major, LargerMinor, SmallerMinor)
#if (LargerMinor < SmallerMinor)
#warning "Value expected for larger minor radius is less than smaller minor
radius. \n"
#warning "Variable radius torus may not be in desired or expected orientation.
\n"
#end // end check minor radius values
#local MajorExtent = (Major + LargerMinor)*1.1;
#local MinorExtent = LargerMinor*2;
#local HalfSum = (LargerMinor + SmallerMinor)/2;
#local HalfDifference = abs(LargerMinor - SmallerMinor)/2;
#local VariableRadiusXY = function (u, v) {(Major + (HalfSum +
cos(u)*HalfDifference)*cos(v) )}
#local VariableRadiusZ = function (u, v) {( (HalfSum +
cos(u)*HalfDifference)*sin(v) )}
parametric {
//function { cos(u) * (Major + (HalfSum + cos(u)*HalfDifference)*cos(v) ) },
// x-axis
function { cos(u) * VariableRadiusXY (u, v) }, // x-axis
function { sin(u) * VariableRadiusXY (u, v) }, // y-axis
function { VariableRadiusZ (u, v) } // z-axis
<0, 0>, <2*pi, 2*pi> // <umin, vmin> to <umax, vmax>
contained_by { box { <-MajorExtent, -MajorExtent, -MinorExtent>, <MajorExtent,
MajorExtent, MinorExtent> } }
// max_gradient 2
accuracy 0.01 // 0.001 default, lower slower but better
precompute 15 x,y,z // precompute [x,y,z] normally gives faster rendering
(<=20)
texture {pigment {color rgb <1, 0, 0> } finish {specular 0.1}}
}
#end // end macro vtorus
object {vtorus (5, 1, 0.5)
rotate z*90
translate -x*2.5
translate z*5
}
object {vtorus (5, 0.5, 1)
rotate z*90
rotate x*80
translate z*5
translate x*2.5
}
#break
#else
// Do nothing
#end // end switch - case/range - break
Post a reply to this message
Attachments:
Download 'dupincyclide.png' (90 KB)
Preview of image 'dupincyclide.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 16/05/2017 à 13:41, Bald Eagle a écrit :
> I didn't have as much time as I would have liked to explore this,
> but after fiddling with the Dupin cyclide in both isosurface (implicit) and
> parametric form, I found the parameters to be highly unintuitive, the desired
> shape very difficult to achieve and control, and the constraints on the
> parameters too complex to be easily implemented.
>
> I hadn't gotten around to unraveling the implicit equation to fit the syntax for
> a polynomial.
I asked the other Internets about that, they had a round tuit left so I
got a nice answer.
> It is, however, SLLLLllllllllllooooooooooowwwwwwww.
It is not slow with a polynomial.
True Duplin Cyclide !
#version 3.7;
global_settings{ assumed_gamma 1.0}
#default { finish { ambient 0.2 diffuse 0.8 } }
#declare HEIGHT=9;
camera { orthographic
location <00,00,30>
up HEIGHT*y
right HEIGHT*image_width/image_height*x
look_at 0
rotate clock*x*90
}
light_source { <20,30,40>,1 }
#declare TC=texture { pigment { color srgb <1,1,1> } };
sphere { 0, 1 texture { TC }}
#declare A=3;
#declare B=A*0.98;
#declare C=sqrt(A*A-B*B);
#declare D=1.3*C;
#declare T=texture { pigment { color srgb <1,0.75,0.5> } };
polynomial{
4,
/* expand (x^2+y^2+z^2+b^2-d^2)^2-4*(a*x-c*d)^2-4*b^2*y^2=0 */
/* -4 a^2 x^2 + 2 b^2 x^2 - 2 d^2 x^2
+ 8 a c d x
+ b^4 - 2 b^2 d^2 - 4 c^2 d^2 + d^4
- 2 b^2 y^2 - 2 d^2 y^2
+ 2 b^2 z^2 - 2 d^2 z^2
+ 2 x^2 y^2
+ 2 x^2 z^2
+ 2 y^2 z^2
+ x^4
+ y^4
+ z^4
= 0
*/
xyz(2,0,0):(-4*A*A)+(2*B*B)-(2*D*D),
xyz(1,0,0):8*A*C*D,
xyz(0,0,0):(B*B*B*B)-(2*B*B*D*D)-(4*C*C*D*D)+(D*D*D*D),
xyz(0,2,0):(-2*B*B)-(2*D*D),
xyz(0,0,2):(2*B*B)-(2*D*D),
xyz(2,2,0):2,
xyz(2,0,2):2,
xyz(0,2,2):2,
xyz(4,0,0):1,
xyz(0,4,0):1,
xyz(0,0,4):1
texture { T }}
Post a reply to this message
Attachments:
Download 'cyclide4.png' (15 KB)
Download 'cyclide3.png' (39 KB)
Download 'cyclide2.png' (59 KB)
Download 'cyclide1.png' (73 KB)
Download 'cyclide0.png' (80 KB)
Preview of image 'cyclide4.png'

Preview of image 'cyclide3.png'

Preview of image 'cyclide2.png'

Preview of image 'cyclide1.png'

Preview of image 'cyclide0.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron <jgr### [at] free fr> wrote:
> Le 16/05/2017 à 13:41, Bald Eagle a écrit :
> > I didn't have as much time as I would have liked to explore this,
> > but after fiddling with the Dupin cyclide in both isosurface (implicit) and
> > parametric form, I found the parameters to be highly unintuitive, the desired
> > shape very difficult to achieve and control, and the constraints on the
> > parameters too complex to be easily implemented.
> >
> > I hadn't gotten around to unraveling the implicit equation to fit the syntax for
> > a polynomial.
> I asked the other Internets about that, they had a round tuit left so I
> got a nice answer.
>
> > It is, however, SLLLLllllllllllooooooooooowwwwwwww.
> It is not slow with a polynomial.
I had wondered / suspected / hoped that were the case.
> True Duplin Cyclide !
That, sir, is a very beautiful thing :)
You did indeed get a very nice answer.
I'm wondering how a, b, c, and d relate to the radii of the shape, and how to
know what values to plug in. The large end always seems to be VERY large
compared to the smaller side, though IIRC, with certain values one can get a
normal torus, so I suppose that might not be inherent in the object.
I found a very interesting paper by Langevin: "Geometry with two screens and
computational graphics" (2014) where he points out some very interesting and
useful properties of the true Dupin cyclide.
Thank you as always, Jerome - and please thank your friends for me as well.
I'm sure I will have some fun playing with this new algebraic surface and
finding ways to harness it in some future scenes. fr> wrote:
> Le 16/05/2017 à 13:41, Bald Eagle a écrit :
> > I didn't have as much time as I would have liked to explore this,
> > but after fiddling with the Dupin cyclide in both isosurface (implicit) and
> > parametric form, I found the parameters to be highly unintuitive, the desired
> > shape very difficult to achieve and control, and the constraints on the
> > parameters too complex to be easily implemented.
> >
> > I hadn't gotten around to unraveling the implicit equation to fit the syntax for
> > a polynomial.
> I asked the other Internets about that, they had a round tuit left so I
> got a nice answer.
>
> > It is, however, SLLLLllllllllllooooooooooowwwwwwww.
> It is not slow with a polynomial.
I had wondered / suspected / hoped that were the case.
> True Duplin Cyclide !
That, sir, is a very beautiful thing :)
You did indeed get a very nice answer.
I'm wondering how a, b, c, and d relate to the radii of the shape, and how to
know what values to plug in. The large end always seems to be VERY large
compared to the smaller side, though IIRC, with certain values one can get a
normal torus, so I suppose that might not be inherent in the object.
I found a very interesting paper by Langevin: "Geometry with two screens and
computational graphics" (2014) where he points out some very interesting and
useful properties of the true Dupin cyclide.
Thank you as always, Jerome - and please thank your friends for me as well.
I'm sure I will have some fun playing with this new algebraic surface and
finding ways to harness it in some future scenes.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
In my quest to parameterize this, I found:
http://or.nsfc.gov.cn/bitstream/00001903-5/173475/1/1000009340012.pdf
Which has some useful information; however, it's stated that:
a,b > 0 and c,f >= 0 are constants.
it goes on to state that it's a ring cyclide if f < c < a.
How can f be less than c if for a torus c=0 and f=r?
(unless of course f < 0)...
it's a normal torus if a=b=R, c=0, and f=r
Currently in the process of expanding the polynomial and grouping to see how a&b
behave when equal, eliminating the c terms, and seeing how f affects the minor
radii of the Dupin cyclide.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 17/05/2017 à 19:05, Bald Eagle a écrit :
> In my quest to parameterize this, I found:
>
> http://or.nsfc.gov.cn/bitstream/00001903-5/173475/1/1000009340012.pdf
>
> Which has some useful information; however, it's stated that:
>
> a,b > 0 and c,f >= 0 are constants.
> it goes on to state that it's a ring cyclide if f < c < a.
>
> How can f be less than c if for a torus c=0 and f=r?
> (unless of course f < 0)...
when c=0, the sign of f( aka d) is irrelevant
(x^2+y^2+z^2+b^2-d^2)^2-4*(a*x-c*d)^2-4*b^2*y^2=0
>
> it's a normal torus if a=b=R, c=0, and f=r
>
>
> Currently in the process of expanding the polynomial and grouping to see how a&b
> behave when equal, eliminating the c terms, and seeing how f affects the minor
> radii of the Dupin cyclide.
>
you already answered that: d(aka f) is then the minor radius, and a=b is
the major radius.
Comparing to the traditional torus equation:
(x^2+y^2+z^2+R^2-r^2)^2-4R^2(x^2+y^2) = 0
the change of radius is due to ax-cd instead of Rx.
Notice that b <= a, and they should be positive, yet c is amongst the
two roots of c^2 = a^2-b^2.
the sign of b is irrelevant, but the sign of a can have an impact with
the sign of c.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
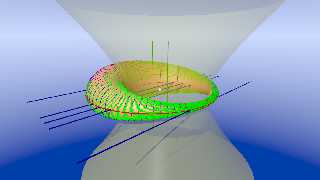
I did a bit of work on this last night, and thanks to
figures 12.21 and 12.22 here:
http://what-when-how.com/computer-graphics-and-geometric-modeling/surfaces-in-computer-graphics-geometric-modeling-part
-7/
I was able to work out some of the circles that lie on the face of the algebraic
surface, the inner ellipse, and the hyperboloid that the surface is tangent to.
It's not perfect - I think there's a little bit of difference due to the scaling
in the z direction due to B=A*0.98, but most of the hard stuff is worked out.
[The x-z plane tori were the hardest to work out. I had a few renders that
looked more like a Hopf Fibration than a Dupin Cyclide. I'll post when I get
some free time ;) ]
I think once I get the Yvon-Vilarceau circles worked out, and everything looking
nice, it will make a nice little macro package.
*
There's a lot of information out there on the cyclides - very interesting work
related to the Appolonian Gasket Soddy Circles, and Soddy's Hexlet - as well as
research into blending surfaces in computer modeling packages - which ought to
be of great interest to those working on creating fillets and smooth transitions
with mathematical primitives.
*
Post a reply to this message
Attachments:
Download 'dupincyclideparameterization.png' (354 KB)
Preview of image 'dupincyclideparameterization.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 18/05/2017 à 13:57, Bald Eagle a écrit :
> I did a bit of work on this last night, and thanks to
>
> figures 12.21 and 12.22 here:
>
http://what-when-how.com/computer-graphics-and-geometric-modeling/surfaces-in-computer-graphics-geometric-modeling-part-7/
>
> I was able to work out some of the circles that lie on the face of the algebraic
> surface, the inner ellipse, and the hyperboloid that the surface is tangent to.
>
> It's not perfect - I think there's a little bit of difference due to the scaling
> in the z direction due to B=A*0.98, but most of the hard stuff is worked out.
Thanks to your link, I would say:
A = R
C = abs(r-rho)/2
B = sqrt(A^2-C^2)
D = (r+rho)/2
with R the traditional radius (major) of the torus
r & rho the two different minor radius
and voila!
Here with 3,2 & 1 (and still the white sphere of radius 1 at origin)
Post a reply to this message
Attachments:
Download 'cyclide0.png' (107 KB)
Download 'cyclide2.png' (76 KB)
Preview of image 'cyclide0.png'

Preview of image 'cyclide2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron <jgr### [at] free fr> wrote:
> Thanks to your link, I would say:
>
> A = R
> C = abs(r-rho)/2
> B = sqrt(A^2-C^2)
> D = (r+rho)/2
>
> with R the traditional radius (major) of the torus
> r & rho the two different minor radius
>
> and voila!
>
> Here with 3,2 & 1 (and still the white sphere of radius 1 at origin)
Yes, excellent - that's the same answer that I came up with, which is also in
agreement with the formulas I came up with for the parametric version.
Hopefully it works without any difficulty. I'll see if I can apply it to the
planetary and satellite orbitals tonight or this weekend. :)
Thanks again! fr> wrote:
> Thanks to your link, I would say:
>
> A = R
> C = abs(r-rho)/2
> B = sqrt(A^2-C^2)
> D = (r+rho)/2
>
> with R the traditional radius (major) of the torus
> r & rho the two different minor radius
>
> and voila!
>
> Here with 3,2 & 1 (and still the white sphere of radius 1 at origin)
Yes, excellent - that's the same answer that I came up with, which is also in
agreement with the formulas I came up with for the parametric version.
Hopefully it works without any difficulty. I'll see if I can apply it to the
planetary and satellite orbitals tonight or this weekend. :)
Thanks again!
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
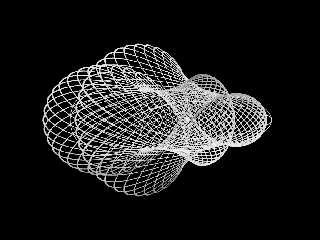
"Bald Eagle" <cre### [at] netscape net> wrote:
> [The x-z plane tori were the hardest to work out. I had a few renders that
> looked more like a Hopf Fibration than a Dupin Cyclide. I'll post when I get
> some free time ;) ] net> wrote:
> [The x-z plane tori were the hardest to work out. I had a few renders that
> looked more like a Hopf Fibration than a Dupin Cyclide. I'll post when I get
> some free time ;) ]
Post a reply to this message
Attachments:
Download 'dupincyclideparameterization - coolmistake.png' (349 KB)
Preview of image 'dupincyclideparameterization - coolmistake.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
2nd:
Post a reply to this message
Attachments:
Download 'dupincyclideparameterization - coolmistake2.png' (336 KB)
Preview of image 'dupincyclideparameterization - coolmistake2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()