I did a bit of work on this last night, and thanks to

figures 12.21 and 12.22   here:
http://what-when-how.com/computer-graphics-and-geometric-modeling/surfaces-in-computer-graphics-geometric-modeling-part
-7/

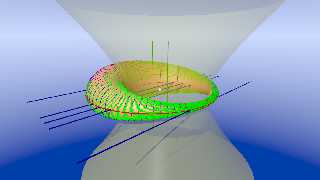
I was able to work out some of the circles that lie on the face of the algebraic
surface, the inner ellipse, and the hyperboloid that the surface is tangent to.

It's not perfect - I think there's a little bit of difference due to the scaling
in the z direction due to B=A*0.98, but most of the hard stuff is worked out.

[The x-z plane tori were the hardest to work out.  I had a few renders that
looked more like a Hopf Fibration than a Dupin Cyclide.  I'll post when I get
some free time  ;) ]

I think once I get the Yvon-Vilarceau circles worked out, and everything looking
nice, it will make a nice little macro package.

*
There's a lot of information out there on the cyclides - very interesting work
related to the Appolonian Gasket Soddy Circles, and Soddy's Hexlet - as well as
research into blending surfaces in computer modeling packages - which ought to
be of great interest to those working on creating fillets and smooth transitions
with mathematical primitives.
*

Post a reply to this message

Attachments:
Download 'dupincyclideparameterization.png' (354 KB)

Preview of image 'dupincyclideparameterization.png'