The catenary is the curve formed by a homogeneous chain suspended between
two points in a uniform gravity field. It looks like a parabola, but it's
mathematically quite different. The equation of a parabola is just
 y = a*x*x, a simple quadratic, whereas a catenary is
 y = a*cosh(x/a), a transcendental equation.

I had occasion to look at Chris Colefax's chain building code in "Linc.inc",
after referring a new user to it, and was dismayed to discover that Chris
used quadratics to build his chains. :(

The Chain() macro below constructs a true catenary. This is a preliminary
draft, so there are no docs as yet, sorry. Read the comments for hints. :)

Any questions and comments are most welcome. Have fun!

//-------------------------------------------------------------------------

// Persistence of Vision Ray Tracer Include File
// File: Catenary.inc
// Vers: 3.6
// Desc: Proper catenary chain.
// Date: 2005.07.30
// Auth: PM 2Ring
//
// Catenary parameter calculations thanks to Zdislav V. Kovarik. See below
//
//-------------------------------------------------------------------------

#ifndef(Catenary_Inc_Temp)
#declare Catenary_Inc_Temp=version;
#version 3.5;

#ifdef(View_POV_Include_Stack)
    #debug "including Catenary.incn"
#end

//-------------------------------------------------------------------------
//
// From: kov### [at] mcmailcisMcMasterCA (Zdislav V. Kovarik)
// Subject: Re: Catenary
// Date: 5 Nov 1999 14:33:22 -0500
// Newsgroups: sci.math
// Keywords: fitting a catenary to match a suspended cable
//
// Upright catenary:  y - y_0 = a * cosh((x - x_0)/a) ,  a > 0.
// The vertex is (x_0, y_0+a).
// The parameter a turns out to be the radius of curvature at the vertex.
// Remark: The radius of curvature at a point above x is
//   a * (cosh((x-x_0)/a)^2.
//
// Problem: Parameters a, x_0, y_0 to be found so that the catenary arc
passes
// through (x_1, y_1), (x_2, y_2) and has length L between these points
// (provided L > sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2) )
//
// The equations to be solved are (after some symmetrizing manipulation
// of the arclength integral)
//
//   y_1 - y_0 = a * cosh ((x_1 - x_0)/a)
//   y_2 - y_0 = a * cosh ((x_2 - x_0)/a)
//   2*a * cosh((x_1 + x_2 - 2*x_0)/(2*a)) * sinh((x_2 - x_1)/(2*a)) = L
//
// and it can be reduced to solving for one unknown at a time.
//
// First, we introduce an auxiliary unknown z which is to satisfy
//
//   sinh(z) / z = sqrt(L^2 - (y_2 - y_1)^2) / abs(x_2 - x_1)  ,   z > 0
//
// (the only transcendental non-elementary equation)
// and then the unknowns pop out:
//
//     a = abs(x_2 - x_1) / (2*z)
//   x_0 = (1/2)*(x_1 + x_2 - a * ln ((L + (y_2 - y_1)) / (L - (y_2 - y_1)))
//   y_0 =  (y_1 + y_2)/2 - (L/2) * coth(z).
//
//-------------------------------------------------------------------------

//Find B such that A=sinh(B)/B. Named in parallel to sinc()
#macro asinch(A)
  #local B = sqrt(6*max(1e-4,A-1));   //1st approx, from sinh(B) = B +
B^3/3! + ...
  #local B = asinh(A*B);              //2nd approx, from sinh(B) = A*B

  #local I = 0;
  #while(I<8)                         //Newton's method
    #local S = sinh(B);
    #local C = B * cosh(B);
    #local M = (A*B + C - 2*S) / (C - S);
    #local B = B * M;
    #local I = I + 1;
    #if(abs(M-1)<1e-12)               //bailout
      #local I=8;
    #end
  #end
  B                                   //return value
#end

//Find width of an object's bounding box
#macro BBWidth(A) (max_extent(A) - min_extent(A)).x #end

//Make a catenary. Parameters: Link object, Start point,End Point,
//Slackness of the chain >1, Link overlap, Extra twist on whole cable
#macro Chain(Link, StartA, EndA, Slack, Overlap, Twist)
  //Temporarily translate to origin & work in XY plane
  #local End = EndA - StartA;
  #local TH = degrees(atan2(End.z, End.x));
  #local End = vrotate(End, y*TH);              //Rotate to positive x-axis

  //Find required chain length and number of links
  #local Len = vlength(End) * Slack;            //Basic chain length
  #local LL = BBWidth(Link) / Overlap;          //Link Length adjusted for
link overlap
  #local Steps = 2*floor(.5*(.5+Len/LL));       //Round up to an even
integer number of links
  #local Len = Steps * LL;                      //Adjusted chain length

  //Find vertex of catenary that connects <0,0,0> & End, with length Len.
  #local P = sqrt(Len*Len - End.y*End.y) / End.x;
  #local Q = asinch(P);
  #local A = End.x / (2*Q);                     //Catenary curvature
parameter.
  #local X = A * ln((Len + End.y) / (Len - End.y));
  #local Y = Len/tanh(Q);
  #local V = (End - <X, Y, 0>)*.5;              //Vertex
  #local S1 = A*sinh(V.x/A);                    //Arclength at vertex

  //Step evenly along catenary parametrized by arclength.
  union {
    #local I=1;
    #while (I<Steps)
      #local S = LL * I - S1;                   //Arclength from Vertex
      #local M = S / A;                         //Slope of tangent
      #local X = asinh(M);
      #local Y = sqrt(1 + M*M);

      object{
        Link
        rotate (90*mod(I+1,2) + Twist*360*(I-1)/(Steps-2))*x
        rotate z*degrees(atan(M))               //Rotate parallel to tangent
        translate V + A*<X, Y, 0>
      }
      #local I=I+1;
    #end

    //Transform back
    rotate -y*TH
    translate StartA
  }
#end

#version Catenary_Inc_Temp;
#end

//-------------------------------------------------------------------------



//-------------------------------------------------------------------------

// Persistence of Vision Ray Tracer Scene Description File
// File: Catenary.pov
// Vers: 3.6
// Desc: Test Catenary include file
// Date: 2005.07.30
// Auth: PM 2Ring
//
// Catenary parameter calculations thanks to Zdislav V. Kovarik
// See Catenary.inc for details.
//
//-------------------------------------------------------------------------
//
// -f -A0.4 +AM2 +R1
// -d +A0.05 +AM2 +R3
//

#include "finish.inc"
#include "metals.inc"

//Chain making macro
#include "Catenary.inc"

global_settings {
  assumed_gamma 1.0
  max_trace_level 25
}

//-------------------------------------------------------------------------

//Simple chain macro. Parameters: Start point,End Point. Make sure other
items are declared before calling!
#macro ChainQ(Start, End) Chain(Link, Start, End, Slack, Overlap, Twist)
#end

//Chain terminal post
#macro Terminal(Pos)
union{
  sphere{Pos, PostRad*1.6}
  cylinder{Pos*<1,0,1>, Pos-0.35*PostRad*y, PostRad}

  pigment{rgb <.2, .5, 1>}
  finish{Glossy}
}
#end

//Chain, with terminal at start
#macro TermChain(Start, End)
  Terminal(Start)
  ChainQ(Start, End)
#end

//Link objects
#declare Torus = torus {.75, .175 scale 0.075*<1, 1, .65> }
#declare Torus1 = object {Torus scale 2 texture{T_Gold_2E} rotate 0*45*x}

//--- The scene -----------------------------------------------------------

#declare Rad = 2.0;               //Scene size control
#declare PostRad= 0.150;          //Post radius

//Chain parameters
#declare Link = Torus1;           //Link object
#declare Slack = 1.12;            //Slackness of the chain. (Length of
chain) / (straight distance between points)
#declare Overlap = 1.65;          //Link overlap
#declare Twist = 0;               //Chain twist (in cycles)

//Points to connect
#declare V1 = < 1.5*Rad, 0.75*Rad, 1>;
#declare V2 = <-1.5*Rad, 1.25*Rad, 3>;

//Do it!
TermChain(V1, V2)
Terminal(V2)

//Simple room with checkered floor
#declare WS = 5*Rad;
box{<-1, -2/WS, -2>, <1, 3, 2> scale WS inverse pigment{gradient y scale
3.001*WS}finish{Shiny}}
box{<-1, -1/WS, -2>, <1, 0, 2> scale WS pigment{checker rgb 1,rgb
....05}finish{Glossy diffuse 0.80}}

camera {
  location <-0.5, 3.5, -5.5> * 0.93 * Rad
  look_at  y*2

  right x*image_width/image_height up y
  direction z

  angle 30
}

light_source {<1, 9, -3>*Rad rgb 1 spotlight point_at z*2 falloff 16 radius
5 }

//-------------------------------------------------------------------------

Post a reply to this message

Attachments:
Download 'catenaryf2.jpg' (100 KB)

Preview of image 'catenaryf2.jpg'

Here's a closeup of a simple glass chain, using the same link as above.
No radiosity, no photons, no dispersion, fake caustics.

Post a reply to this message

Attachments:
Download 'catenarye5k.png' (174 KB)

Preview of image 'catenarye5k.png'

PM 2Ring wrote:
> The catenary is the curve formed by a homogeneous chain suspended
> between two points in a uniform gravity field. It looks like a
> parabola, but it's mathematically quite different. The equation of a
>  parabola is just y = a*x*x, a simple quadratic, whereas a catenary is
>  y = a*cosh(x/a), a transcendental equation.
>
> I had occasion to look at Chris Colefax's chain building code in
> "Linc.inc", after referring a new user to it, and was dismayed to
> discover that Chris used quadratics to build his chains. :(

IIRC the "quadratic" chain assumes even weight distribution in the
horizontal direction, whereas the catenary takes account of the fact that a
chain at a steep angle will be heavier per unit horizontal distance.
Clearly the steeper the chain the more of an "error" the quadratic one has.

How about a comparison between the two for different length chains between
two points?

Post a reply to this message

"scott" <sco### [at] spamcom> wrote:
> PM 2Ring wrote:
> > The catenary is the curve formed by a homogeneous chain suspended
> > between two points in a uniform gravity field. It looks like a
> > parabola, but it's mathematically quite different. The equation of a
> >  parabola is just y = a*x*x, a simple quadratic, whereas a catenary is
> >  y = a*cosh(x/a), a transcendental equation.
> >
> > I had occasion to look at Chris Colefax's chain building code in
> > "Linc.inc", after referring a new user to it, and was dismayed to
> > discover that Chris used quadratics to build his chains. :(
>
> IIRC the "quadratic" chain assumes even weight distribution in the
> horizontal direction, whereas the catenary takes account of the fact that a
> chain at a steep angle will be heavier per unit horizontal distance.
> Clearly the steeper the chain the more of an "error" the quadratic one has.

Yes, the parabola is the curve of a suspension bridge with uniform
horizontal load.

> How about a comparison between the two for different length chains between
> two points?

I've been thinking about doing this, so I'll put something together over the
next day or so. It may be a little bit tricky ensuring both chains are
identical in length... it should be ok if I use very small links, though.
I also want to see the difference between the parabola & catenary with
connection points at unequal heights.

Thanks for your feedback, scott.

Post a reply to this message

PM 2Ring wrote:
> Here's a closeup of a simple glass chain, using the same link as above.
> No radiosity, no photons, no dispersion, fake caustics.
> 
> 
> ------------------------------------------------------------------------
> 
Beautiful.

Post a reply to this message

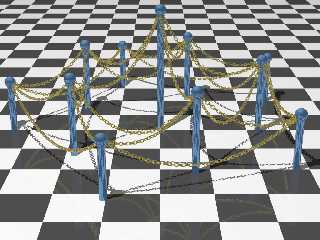
Here are a few positioning macros (and an iron link I borrowed from Chris
Colefax's Link.inc). The attached image is from a slightly different view
location & probably using links of a different size.

//-------------------------------------------------------------------------

// Persistence of Vision Ray Tracer Scene Description File
// File: Catenary.pov
// Vers: 3.6
// Desc: Catenaries between multiple poles arranged in polygons
// Date: 2005.07.30
// Auth: PM 2Ring
//
// -f +A0.4 +AM2 +R1
// -d +A0.2 +AM2 +R4
// -d +A0.1 +AM2 +R3
// -d +A0.05 +AM2 +R3
//

//Chain making macro
#include "Catenary.inc"

global_settings {
  assumed_gamma 1.0
  max_trace_level 25
}

//Textures ----------------------------------------

#declare Shiny =
finish{
  phong .35 phong_size 320
  ambient 0.1 diffuse 0.85 reflection 0.15
}

#declare TChain =
texture{
  //pigment{rgb 1}
  pigment{rgb <1, .8, .15>}
  finish{Shiny metallic
  diffuse 0.25 brilliance 7 reflection {0.55, .65 metallic}
  }
}

#declare TTerminal =
texture{
  //pigment{rgb 1}
  pigment{rgb <.2, .5, 1>}
  finish{
    Shiny
    reflection {0.35,.45 metallic} diffuse 0.4 brilliance 5
  }
}

//-------------------------------------------------------------------------

//Link objects
#declare Torus1 = torus {.75, .175 scale 0.05*<1, 1, .65> texture{TChain}}

//From LinkObjs.inc by Chris Colefax
#declare Iron_Chain =
union {
  torus {.7, .3 clipped_by {box {<-1, -.3, -1>, <0, .3, 1>}} translate -x *
.....6}
  torus {.7, .3 clipped_by {box {<-1, -.3, -1>, <0, .3, 1>}} translate -x *
.....6 scale <-1, 1, 1>}
  cylinder {-x*.6, x*.6, .3 translate z * .7}
  cylinder {-x*.6, x*.6, .3 translate -z * .7}
  pigment {rgb <.4, .4, .45>} normal {dents .6 scale .3} finish {phong .3
phong_size 10 metallic}
  scale .035
}

//-------------------------------------------------------------------------

//Simple chain macro. Parameters: Start point,End Point. Make sure other
items are declared before calling!
#macro ChainQ(Start, End) Chain(Link, Start, End, Slack, Overlap, Twist)
#end
//#macro ChainQ(Start, End)#end  //No Chains!

//Chain terminal post
#macro Terminal(Pos)
union{
  sphere{Pos, PostRad*1.6}
  cylinder{Pos*<1,0,1>, Pos-0.35*PostRad*y, PostRad}

  pigment{rgb <.2, .5, 1>}
  texture{TTerminal}
}
#end

//Chain, with terminal at start
#macro TermChain(Start, End)
  Terminal(Start)
  ChainQ(Start, End)
#end

//-Positioning
macros--------------------------------------------------------

//Connect all points in PosList with chain. Terminate if not a ring.
#macro MultiChain(PosList)
  #local N=dimension_size(PosList,1);
  #local I=0;
  #while(I<N-1)
    #local Start = PosList[I];
    #local End = PosList[I+1];
      TermChain(Start, End)
    #local I=I+1;
  #end

  #if(vlength(End-PosList[0]))
    Terminal(End)
  #end
#end

//Connect all points in PosList to a centre post
#macro CenterChain(PosList)
  #local N=dimension_size(PosList,1);
  #local I=0;
  #local End = <0, 1.25*Rad, 0>;
  #while(I<N-1)
    #local Start = PosList[I];
    ChainQ(Start, End)
    #local I=I+1;
  #end

  Terminal(End)
#end

//Connect all points in PosList0 to Poslist1, like threading shoelaces. No
error checking!
#macro ThreadChain(PosList0, PosList1)
  #local N=dimension_size(PosList0,1);
  #local I=0;
  #while(I<N)
    #local Start = PosList0[I];
    #local End = PosList1[I];
    ChainQ(Start, End)

    #local Start = PosList0[mod(I+1,N)];
    ChainQ(Start, End)

    #local I=I+1;
  #end
#end

// The scene ----------------------------------------

#declare Rad = 2.25;

//Link object
#declare Link = Torus1;
//#declare Link = Iron_Chain;

#declare Slack=1.35;       // Slackness of the chain
#declare Overlap=1.60;     //Link overlap
#declare Twist = 0;               //Chain twist (in cycles)

#declare PostRad=.05;      //Post radius
#declare MI = 5;           //Polygon sides
#declare InRing = array[MI+1];
#declare OutRing = array[MI+1];

#declare I=0;
#declare DT=pi/MI;
#while (I<=MI)
  #declare T = 2 * pi * I/MI;
  #declare InRing[I] = Rad*<cos(T), 0.75, sin(T)>;
  #declare OutRing[I] = 1.5*Rad*<cos(T+DT), .35, sin(T+DT)>;
  #declare I=I+1;
#end
MultiChain(InRing)

#declare Slack = Slack / 1.1;
CenterChain(InRing)

#declare Slack = Slack / 1.1;
MultiChain(OutRing)
ThreadChain(InRing, OutRing)

//Simple room with checkered floor
#declare WS = 4*Rad;
box{<-1, -2/WS, -2>, <1, 3, 2> scale WS inverse pigment{gradient y scale
3.001*WS}}
box{<-1, -1/WS, -2>, <1, 0, 2> scale WS pigment{checker rgb 1,rgb
...05}finish{Shiny}}

camera {
  location <1, 4.5, -10> * 1.25
  look_at  y*0.50
  angle 30
}

light_source {<-2, 8, -3>*2 rgb 1}

// ----------------------------------------

Post a reply to this message

Attachments:
Download 'catenaryd1.jpg' (170 KB)

Preview of image 'catenaryd1.jpg'

"Sebastian H." <van### [at] gmxde> wrote:
> PM 2Ring wrote:
> > Here's a closeup of a simple glass chain, using the same link as above.
> > No radiosity, no photons, no dispersion, fake caustics.
> >
> >
> > ------------------------------------------------------------------------
> >
> Beautiful.

Thankyou, Sebastian! Now I'll *have* to do one with more realistic glass, or
maybe even diamond. :) I'll have to do it on my machine at work, this old
beast would take days.

Post a reply to this message

"PM 2Ring" <nomail@nomail> wrote in message
news:web.42edf3bf208413009143b5c90@news.povray.org...
> The catenary is the curve formed by a homogeneous chain suspended between
> two points in a uniform gravity field. It looks like a parabola, but it's
> mathematically quite different. The equation of a parabola is just
>  y = a*x*x, a simple quadratic, whereas a catenary is
>  y = a*cosh(x/a), a transcendental equation.
>
> I had occasion to look at Chris Colefax's chain building code in
"Linc.inc",
> after referring a new user to it, and was dismayed to discover that Chris
> used quadratics to build his chains. :(
>
> The Chain() macro below constructs a true catenary. This is a preliminary
> draft, so there are no docs as yet, sorry. Read the comments for hints. :)
>
> Any questions and comments are most welcome. Have fun!

Cool cool. I think about this occasionally, probably everytime i see a
cosh()  for some reason. This is the same curve that would describe wires
between telephone poles, right?

anyway, neat work. i await the realistic glass render although the fake
glass looked pretty too :)

Post a reply to this message

Ross nous apporta ses lumieres en ce 2005-08-01 12:00:

> 
> Cool cool. I think about this occasionally, probably everytime i see a
> cosh()  for some reason. This is the same curve that would describe wires
> between telephone poles, right?
> 
> anyway, neat work. i await the realistic glass render although the fake
> glass looked pretty too :)
> 
> 
> 
This is indeed the curve of any whire, string, rope or chain suspended between two
points. This 
assuming that the whire is not to stiff relative to it's weith and length.

Alain

Post a reply to this message

"Ross" <rli### [at] everestkcnet> wrote:
> "PM 2Ring" <nomail@nomail> wrote in message
> news:web.42edf3bf208413009143b5c90@news.povray.org...
> > The catenary is the curve formed by a homogeneous chain suspended between
> > two points in a uniform gravity field. It looks like a parabola, but it's
> > mathematically quite different. The equation of a parabola is just
> >  y = a*x*x, a simple quadratic, whereas a catenary is
> >  y = a*cosh(x/a), a transcendental equation.
> >
> > I had occasion to look at Chris Colefax's chain building code in
> "Linc.inc",
> > after referring a new user to it, and was dismayed to discover that Chris
> > used quadratics to build his chains. :(
> >
> > The Chain() macro below constructs a true catenary. This is a preliminary
> > draft, so there are no docs as yet, sorry. Read the comments for hints. :)
> >
> > Any questions and comments are most welcome. Have fun!
>
> Cool cool. I think about this occasionally, probably everytime i see a
> cosh()  for some reason. This is the same curve that would describe wires
> between telephone poles, right?

Yes, and catenary arches are very strong, too. Also, a catenary rotated
around the X-axis makes a catenoid, the shape of a soap-film between a pair
of parallel circular loops.

> anyway, neat work. i await the realistic glass render although the fake
> glass looked pretty too :)

Here's a more realistic one, with radiosity & dispersion. I'm doing one now
with photons; I assume it will take all weekend.

Post a reply to this message

Attachments:
Download 'catenaryea1.jpg' (78 KB)

Preview of image 'catenaryea1.jpg'