 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
This had some interesting data on the equations for the 1st and 2nd derivatives
of the curves, so I'm just going to drop this here.
https://www.codeproject.com/Articles/31859/Draw-a-Smooth-Curve-through-a-Set-of-2D-Points-wit
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>
> > I assume that you are looking at my 'Bezier_Patches_Stitched' files.
>
> Yes. They were, in fact, the motivation for my original attempts at stitching
> 9 patches together.
>...
=)
>...
> How did you smoothly connect the corner points in
> http://news.povray.org/web.5b7398619b869b61264be49d0%40news.povray.org ?
> Is that a bezier spline sphere-sweep?
> [Is it /beh-ZHEER/?]
Yes, that was done with sphere sweeps. As I have not found a Bezier type spline
in POV-Ray, I used linear_spline sphere_sweeps with many points placed along a
Bezier curve (that I calculated with some self made Bezier functions).
From your later posts in this thread it seems like you have now figured out how
to do something similar.
Anyway, for others that may be interested, I've attached an image which shows
which contol points to use for these "cubic Bezier sphere sweeps". I've colored
the relevant "sweeps" red and their control points green.
> I spent some time pondering the boundary conditions, and how to process 16
> patches like the stitched renders.
> What I've come up with is to
> create an array of 25 corner points
> create an array of 16 points, and "copy" the relevant corner points into the
> appropriate places
> calculate the linear vectors between the corners of each side
> set the control points on those sides to 1/3 and 2/3 of the vector
> Use those control points to interpolate the 4 inner control points in an
> analogous manner
I'm not sure if I follow you, but some of it sounds ok.
> I hope to get a little bit more time tonight to try and implement that, and see
> how it goes.
>
> Then I can start to think about how to write a macro and set up a data structure
> to instantiate arbitrarily selected patches, given the corner points. It's the
> lone corners and edges that might be tricky for me.
>...
Yes, be very careful with what you do at the corners and along the edges.
> Now, having better grasped what you were doing here, I'd say that based on my
> reading, this would give "G1 continuity".
Yes, that is also my understanding.
Here's more theory about this:
https://people.eecs.berkeley.edu/~sequin/CS284/LECT12/L4.html
> I think that my first time approaching this, I was trying to use 3x3 patches to
> give 4 control points and then do deCastejau to subdivide the super-pseudo
> Bezier spline suggested by those 4 points so that I could interpolate the inner
> control points of the edges in a "Bezier manner", if that makes sense.
When experimenting with these Bezier curves and patches I find it easier to use
Bernstein polynomials than to use de Castejau's algorithm.
>...
--
Tor Olav
http://subcube.com com> wrote:
>
> > I assume that you are looking at my 'Bezier_Patches_Stitched' files.
>
> Yes. They were, in fact, the motivation for my original attempts at stitching
> 9 patches together.
>...
=)
>...
> How did you smoothly connect the corner points in
> http://news.povray.org/web.5b7398619b869b61264be49d0%40news.povray.org ?
> Is that a bezier spline sphere-sweep?
> [Is it /beh-ZHEER/?]
Yes, that was done with sphere sweeps. As I have not found a Bezier type spline
in POV-Ray, I used linear_spline sphere_sweeps with many points placed along a
Bezier curve (that I calculated with some self made Bezier functions).
From your later posts in this thread it seems like you have now figured out how
to do something similar.
Anyway, for others that may be interested, I've attached an image which shows
which contol points to use for these "cubic Bezier sphere sweeps". I've colored
the relevant "sweeps" red and their control points green.
> I spent some time pondering the boundary conditions, and how to process 16
> patches like the stitched renders.
> What I've come up with is to
> create an array of 25 corner points
> create an array of 16 points, and "copy" the relevant corner points into the
> appropriate places
> calculate the linear vectors between the corners of each side
> set the control points on those sides to 1/3 and 2/3 of the vector
> Use those control points to interpolate the 4 inner control points in an
> analogous manner
I'm not sure if I follow you, but some of it sounds ok.
> I hope to get a little bit more time tonight to try and implement that, and see
> how it goes.
>
> Then I can start to think about how to write a macro and set up a data structure
> to instantiate arbitrarily selected patches, given the corner points. It's the
> lone corners and edges that might be tricky for me.
>...
Yes, be very careful with what you do at the corners and along the edges.
> Now, having better grasped what you were doing here, I'd say that based on my
> reading, this would give "G1 continuity".
Yes, that is also my understanding.
Here's more theory about this:
https://people.eecs.berkeley.edu/~sequin/CS284/LECT12/L4.html
> I think that my first time approaching this, I was trying to use 3x3 patches to
> give 4 control points and then do deCastejau to subdivide the super-pseudo
> Bezier spline suggested by those 4 points so that I could interpolate the inner
> control points of the edges in a "Bezier manner", if that makes sense.
When experimenting with these Bezier curves and patches I find it easier to use
Bernstein polynomials than to use de Castejau's algorithm.
>...
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'control_points_for_cubic_bezier_splines_along_edges_of_bicubic_bezier_patches.jp.jpg' (253 KB)
Preview of image 'control_points_for_cubic_bezier_splines_along_edges_of_bicubic_bezier_patches.jp.jpg'
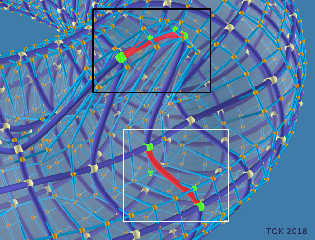
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> Given that a Bezier patch can be interpreted as a Bezier spline in one dimension
> whose control points slide along Bezier splines oriented in the other dimension,
> and that this can be expressed as a parametiric equation, then
>
> It ought to be possible to define a parametric {} object in POV-Ray based on a
> set of control points and the basis functions of the Bezier splines.
>...
Yes, that is possible. Just create 3 bivariate functions with the appropriate
Bernstein polynomials and feed them to the parametric object. But you need
patience for that...
> Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> the surface of the patch.
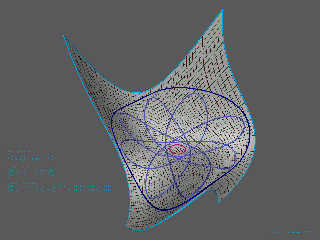
Yes, this image shows some white spheres and cylinders following a path in the
UV-space on the surface of a NURBS-patch:
http://dataduppedings.no/subcube/POV-Ray_Images/NURBS_Grid.jpg
See also the attached image where the I've put some sphere sweeps on a Bezier
patch. (Notice that you can read out the radii for the sphere swept curves
(0.06, 0.46 and 0.48) in the UV-mapped texture.)
>...
--
Tor Olav
http://subcube.com net> wrote:
>...
> Given that a Bezier patch can be interpreted as a Bezier spline in one dimension
> whose control points slide along Bezier splines oriented in the other dimension,
> and that this can be expressed as a parametiric equation, then
>
> It ought to be possible to define a parametric {} object in POV-Ray based on a
> set of control points and the basis functions of the Bezier splines.
>...
Yes, that is possible. Just create 3 bivariate functions with the appropriate
Bernstein polynomials and feed them to the parametric object. But you need
patience for that...
> Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> the surface of the patch.
Yes, this image shows some white spheres and cylinders following a path in the
UV-space on the surface of a NURBS-patch:
http://dataduppedings.no/subcube/POV-Ray_Images/NURBS_Grid.jpg
See also the attached image where the I've put some sphere sweeps on a Bezier
patch. (Notice that you can read out the radii for the sphere swept curves
(0.06, 0.46 and 0.48) in the UV-mapped texture.)
>...
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'sphere sweeps on a bicubic bezier patch.jpg' (333 KB)
Preview of image 'sphere sweeps on a bicubic bezier patch.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> Given that a Bezier patch can be interpreted as a Bezier spline in one dimension
> whose control points slide along Bezier splines oriented in the other dimension,
> and that this can be expressed as a parametiric equation, then
>
> It ought to be possible to define a parametric {} object in POV-Ray based on a
> set of control points and the basis functions of the Bezier splines.
>
> Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> the surface of the patch.
>
> This should also allow the generation of _any_ spline between the ordinate /
> cardinal splines defined by the corners. In theory one should be able to
> simulate a patch by juxtaposing a series of splines from one side to the other
> in either dimension.
If you calculate the two partial derivatives (d/dU and d/dV) for each of the
bivariate functions for a Bezier patch you can use these to reorient objects to
align with the U-, V- and normal directions of the surface.
This article contains some useful information about that:
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
The attached image shows cubes that are reoriented to align with the directions
I mentioned above. It also shows a lot of splines that creates a grid on the
surface of the patch.
>...
--
Tor Olav
http://subcube.com net> wrote:
>...
> Given that a Bezier patch can be interpreted as a Bezier spline in one dimension
> whose control points slide along Bezier splines oriented in the other dimension,
> and that this can be expressed as a parametiric equation, then
>
> It ought to be possible to define a parametric {} object in POV-Ray based on a
> set of control points and the basis functions of the Bezier splines.
>
> Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> the surface of the patch.
>
> This should also allow the generation of _any_ spline between the ordinate /
> cardinal splines defined by the corners. In theory one should be able to
> simulate a patch by juxtaposing a series of splines from one side to the other
> in either dimension.
If you calculate the two partial derivatives (d/dU and d/dV) for each of the
bivariate functions for a Bezier patch you can use these to reorient objects to
align with the U-, V- and normal directions of the surface.
This article contains some useful information about that:
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
The attached image shows cubes that are reoriented to align with the directions
I mentioned above. It also shows a lot of splines that creates a grid on the
surface of the patch.
>...
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'cubes on the surface of a bicubic bezier patch.jpg' (432 KB)
Preview of image 'cubes on the surface of a bicubic bezier patch.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> "Bald Eagle" <cre### [at] netscape com> wrote:
> "Bald Eagle" <cre### [at] netscape net> wrote:
> >...
>...
> If you calculate the two partial derivatives (d/dU and d/dV) for each of the
> bivariate functions for a Bezier patch you can use these to reorient objects to
> align with the U-, V- and normal directions of the surface.
>
> This article contains some useful information about that:
>
>
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
>
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
Here's another image where the cubes have been scaled in the U/V-directions by
the lengths of the vectors used for reorienting them. (These vectors were
created with the partial derivatives of the bivariate functions for the Bezier
patch.)
--
Tor Olav
http://subcube.com net> wrote:
> >...
>...
> If you calculate the two partial derivatives (d/dU and d/dV) for each of the
> bivariate functions for a Bezier patch you can use these to reorient objects to
> align with the U-, V- and normal directions of the surface.
>
> This article contains some useful information about that:
>
>
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
>
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
Here's another image where the cubes have been scaled in the U/V-directions by
the lengths of the vectors used for reorienting them. (These vectors were
created with the partial derivatives of the bivariate functions for the Bezier
patch.)
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'scaled_cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg' (426 KB)
Preview of image 'scaled_cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>...
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
I don't know why the preview of that image is not shown properly. (Perhaps the
height/width-dimensions are too big ?). Here's a try with smaller dimensions.
--
Tor Olav
http://subcube.com com> wrote:
>...
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
I don't know why the preview of that image is not shown properly. (Perhaps the
height/width-dimensions are too big ?). Here's a try with smaller dimensions.
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg' (172 KB)
Preview of image 'cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>...
> Here's another image where the cubes have been scaled in the U/V-directions by
> the lengths of the vectors used for reorienting them. (These vectors were
> created with the partial derivatives of the bivariate functions for the Bezier
> patch.)
Here's the same image with smaller dimensions.
--
Tor Olav
http://subcube.com com> wrote:
>...
> Here's another image where the cubes have been scaled in the U/V-directions by
> the lengths of the vectors used for reorienting them. (These vectors were
> created with the partial derivatives of the bivariate functions for the Bezier
> patch.)
Here's the same image with smaller dimensions.
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'scaled_cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg' (165 KB)
Preview of image 'scaled_cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> Yes, that is possible. Just create 3 bivariate functions with the appropriate
> Bernstein polynomials and feed them to the parametric object. But you need
> patience for that...
Pffft. Then forget it. None of us Povvers have any patience for that kind of
thing..
We want the instant gratification of hand-coding 1776 lines of SDL that hands us
that first frame of a 3600-frame animation by the very next day!
> > Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> > the surface of the patch.
>
> Yes, this image shows some white spheres and cylinders following a path in the
> UV-space on the surface of a NURBS-patch:
>
> http://dataduppedings.no/subcube/POV-Ray_Images/NURBS_Grid.jpg
Right - I've admired that one also.
I haven't yet gotten to coding any NURBS objects - but I'm sure it's an
inevitability ;)
> See also the attached image where the I've put some sphere sweeps on a Bezier
> patch. (Notice that you can read out the radii for the sphere swept curves
> (0.06, 0.46 and 0.48) in the UV-mapped texture.)
Yes - that's a neat trick. I can already see the 2 rotating sets of rolling
spheres in a bowl-shaped Bezier patch, oscillating in simple harmonic motion.
Very nice images as always - you surely have some great macros worked out in
order to be able to make all these "custom" renders in short order. com> wrote:
> Yes, that is possible. Just create 3 bivariate functions with the appropriate
> Bernstein polynomials and feed them to the parametric object. But you need
> patience for that...
Pffft. Then forget it. None of us Povvers have any patience for that kind of
thing..
We want the instant gratification of hand-coding 1776 lines of SDL that hands us
that first frame of a 3600-frame animation by the very next day!
> > Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> > the surface of the patch.
>
> Yes, this image shows some white spheres and cylinders following a path in the
> UV-space on the surface of a NURBS-patch:
>
> http://dataduppedings.no/subcube/POV-Ray_Images/NURBS_Grid.jpg
Right - I've admired that one also.
I haven't yet gotten to coding any NURBS objects - but I'm sure it's an
inevitability ;)
> See also the attached image where the I've put some sphere sweeps on a Bezier
> patch. (Notice that you can read out the radii for the sphere swept curves
> (0.06, 0.46 and 0.48) in the UV-mapped texture.)
Yes - that's a neat trick. I can already see the 2 rotating sets of rolling
spheres in a bowl-shaped Bezier patch, oscillating in simple harmonic motion.
Very nice images as always - you surely have some great macros worked out in
order to be able to make all these "custom" renders in short order.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> If you calculate the two partial derivatives (d/dU and d/dV) for each of the
> bivariate functions for a Bezier patch you can use these to reorient objects to
> align with the U-, V- and normal directions of the surface.
One more thing to ponder the full import of.
Just keep raising the bar. :P
> This article contains some useful information about that:
>
>
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
I do believe I've seen that one, but haven't had the time to fullly dissect and
digest it.
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
Well, assuming the patch is bounded by a unit sphere, then those are ---
subcubes.
:D
I have a vague notion that some of this might be accomplished via matrix
transforms. But that's only a tenuous supposition at this point.
....
Care to make a MEDIA Bezier patch? :) com> wrote:
> If you calculate the two partial derivatives (d/dU and d/dV) for each of the
> bivariate functions for a Bezier patch you can use these to reorient objects to
> align with the U-, V- and normal directions of the surface.
One more thing to ponder the full import of.
Just keep raising the bar. :P
> This article contains some useful information about that:
>
>
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
I do believe I've seen that one, but haven't had the time to fullly dissect and
digest it.
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
Well, assuming the patch is bounded by a unit sphere, then those are ---
subcubes.
:D
I have a vague notion that some of this might be accomplished via matrix
transforms. But that's only a tenuous supposition at this point.
....
Care to make a MEDIA Bezier patch? :)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 23/08/2018 à 00:59, Bald Eagle a écrit :
> Right - I've admired that one also.
> I haven't yet gotten to coding any NURBS objects - but I'm sure it's an
> inevitability ;)
If you can find a modeller from which you can export the two
knot-vectors and the grid of of weighted control points, I would be very
interested.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()