 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> Last night, I dreamed about Klein Bottles. That would be a hellish job
> to model I guess. ;-)
Probably pour a hell of a cocktail too :)
I was actually inspecting TOK's tori more closely to to try and understand where
my first attempt (this round) went off the rails. I think it's because I kept
all my data isolated to the patch instead of "looking over" to see if there was
another patch adjacent to that edge.
And that got me thinking about how he automates the patching of a torus - and
the kind of data structure and algorithms that are needed.
I think I get it. I also think I might need to write some macros to do things
with arrays that we don't have yet, or that can only be done "the long way" - so
macros it is.
Thanks for the kind words. It's been slow going.
It seems like there are a few projects hovering around some common things, and
it would be great if there were some breakthroughs and they could coalesce.
Very interested in JimT's work on the triangular patch, and BGimeno's excellent
patterned tori. I think the triangular patch would open up some new
possibilities, or at least make them easier to implement. org> wrote:
> Last night, I dreamed about Klein Bottles. That would be a hellish job
> to model I guess. ;-)
Probably pour a hell of a cocktail too :)
I was actually inspecting TOK's tori more closely to to try and understand where
my first attempt (this round) went off the rails. I think it's because I kept
all my data isolated to the patch instead of "looking over" to see if there was
another patch adjacent to that edge.
And that got me thinking about how he automates the patching of a torus - and
the kind of data structure and algorithms that are needed.
I think I get it. I also think I might need to write some macros to do things
with arrays that we don't have yet, or that can only be done "the long way" - so
macros it is.
Thanks for the kind words. It's been slow going.
It seems like there are a few projects hovering around some common things, and
it would be great if there were some breakthroughs and they could coalesce.
Very interested in JimT's work on the triangular patch, and BGimeno's excellent
patterned tori. I think the triangular patch would open up some new
possibilities, or at least make them easier to implement.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thinking about this a little more - and thinking back, it was a combination of
TOK's work and the question about the vibrating plate that combined to start me
investigating how to control a bicubic patch - or a network of them - such that
the surface could be made to intersect specifically designated points.
Going in the opposite direction:
(ignoring trace(), and approaching this a priori / ab initio)
Given that a Bezier patch can be interpreted as a Bezier spline in one dimension
whose control points slide along Bezier splines oriented in the other dimension,
and that this can be expressed as a parametiric equation, then
It ought to be possible to define a parametric {} object in POV-Ray based on a
set of control points and the basis functions of the Bezier splines.
Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
the surface of the patch.
This should also allow the generation of _any_ spline between the ordinate /
cardinal splines defined by the corners. In theory one should be able to
simulate a patch by juxtaposing a series of splines from one side to the other
in either dimension.
I think that it also might be possible to define an isosurface {} in the same
way, and since there's a method for creating offset surfaces with isosurfaces,
then I'd be interested in seeing what's possible with a 3D rectangular mesh
skinned in Bezier patches and making a thickened hollow shell by that method.
Just some thoughts.
I also have a question that I have not answered for myself yet - is there a type
of spline that is coincident with a Bezier spline, but that contains / is
coincident with its own control points?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> I just added some code to draw the Bezier splines across the patch, using Cousin
> Ricky's spheresweep.inc v1.2 from the Object Collection.
>
> The splines don't quite line up - but I suppose, more concerning is that the
> splines don't intersect with the corner points.
>
> Probably just some wee little bug in there somewhere.
> I'm using the web interface, so I can't rename the message title.
>
> MAYBE I might try to code up a quick Bezier spline macro, if the formula I found
> here:
> http://wiki.povray.org/content/HowTo:Use_Splines_and_Bezier_Curves
> (with the bad math code)
> is correct.
>
> P(t) = A*pow((1-t),3) + 3*B*t*pow((1-t),2) + 3*C*pow(t,2)*(1-t) + D*pow(t,3)
>
> which seems to jive with
> http://idav.ucdavis.edu/education/CAGDNotes/Matrix-Cubic-Bezier-Curve/img1.gif
I explain why I did it the way I did in p.o-c:
On 2015-09-11 08:21 PM (-4), Cousin Ricky wrote:
>
> My calculation uses brute force rather than the single reduced formula
> with all the pow() calls. This was because my ability to concentrate is
> so bad nowadays that I just gave up on trying to figure it out. I
> figured that the internal math of the reduced formula would be more
> complicated anyway. Had I known how simple the final formula was, and
> recalled Clipka's observation that the complexity of the SDL always
> trumps the math, I would have taken that route. However, the parse time
> is so short, there would be little difference either way.
Rewriting the code to match the reduced formula might give people peace of mind
that my SDL is correct, but as long as the current version works, there's no
urgency to mess with it. net> wrote:
> I just added some code to draw the Bezier splines across the patch, using Cousin
> Ricky's spheresweep.inc v1.2 from the Object Collection.
>
> The splines don't quite line up - but I suppose, more concerning is that the
> splines don't intersect with the corner points.
>
> Probably just some wee little bug in there somewhere.
> I'm using the web interface, so I can't rename the message title.
>
> MAYBE I might try to code up a quick Bezier spline macro, if the formula I found
> here:
> http://wiki.povray.org/content/HowTo:Use_Splines_and_Bezier_Curves
> (with the bad math code)
> is correct.
>
> P(t) = A*pow((1-t),3) + 3*B*t*pow((1-t),2) + 3*C*pow(t,2)*(1-t) + D*pow(t,3)
>
> which seems to jive with
> http://idav.ucdavis.edu/education/CAGDNotes/Matrix-Cubic-Bezier-Curve/img1.gif
I explain why I did it the way I did in p.o-c:
On 2015-09-11 08:21 PM (-4), Cousin Ricky wrote:
>
> My calculation uses brute force rather than the single reduced formula
> with all the pow() calls. This was because my ability to concentrate is
> so bad nowadays that I just gave up on trying to figure it out. I
> figured that the internal math of the reduced formula would be more
> complicated anyway. Had I known how simple the final formula was, and
> recalled Clipka's observation that the complexity of the SDL always
> trumps the math, I would have taken that route. However, the parse time
> is so short, there would be little difference either way.
Rewriting the code to match the reduced formula might give people peace of mind
that my SDL is correct, but as long as the current version works, there's no
urgency to mess with it.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Cousin Ricky" <rickysttATyahooDOTcom> wrote:
> I explain why I did it the way I did in p.o-c:
Yes, I read that part - no complaints here.
I'm very happy with what you were able to achieve - I read through the code, and
it's pretty impressive.
You still have 1000x times the drive and attention span of most people.
> Rewriting the code to match the reduced formula might give people peace of mind
> that my SDL is correct, but as long as the current version works, there's no
> urgency to mess with it.
"Never worry about theory as long as the machinery does what it's supposed to
do." - Robert A. Heinlein
Again, excellent work - it does exactly what I need it to do. :)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
This had some interesting data on the equations for the 1st and 2nd derivatives
of the curves, so I'm just going to drop this here.
https://www.codeproject.com/Articles/31859/Draw-a-Smooth-Curve-through-a-Set-of-2D-Points-wit
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>
> > I assume that you are looking at my 'Bezier_Patches_Stitched' files.
>
> Yes. They were, in fact, the motivation for my original attempts at stitching
> 9 patches together.
>...
=)
>...
> How did you smoothly connect the corner points in
> http://news.povray.org/web.5b7398619b869b61264be49d0%40news.povray.org ?
> Is that a bezier spline sphere-sweep?
> [Is it /beh-ZHEER/?]
Yes, that was done with sphere sweeps. As I have not found a Bezier type spline
in POV-Ray, I used linear_spline sphere_sweeps with many points placed along a
Bezier curve (that I calculated with some self made Bezier functions).
From your later posts in this thread it seems like you have now figured out how
to do something similar.
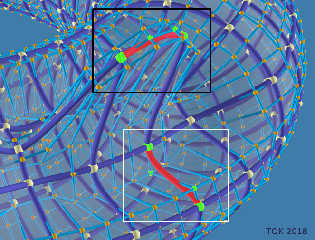
Anyway, for others that may be interested, I've attached an image which shows
which contol points to use for these "cubic Bezier sphere sweeps". I've colored
the relevant "sweeps" red and their control points green.
> I spent some time pondering the boundary conditions, and how to process 16
> patches like the stitched renders.
> What I've come up with is to
> create an array of 25 corner points
> create an array of 16 points, and "copy" the relevant corner points into the
> appropriate places
> calculate the linear vectors between the corners of each side
> set the control points on those sides to 1/3 and 2/3 of the vector
> Use those control points to interpolate the 4 inner control points in an
> analogous manner
I'm not sure if I follow you, but some of it sounds ok.
> I hope to get a little bit more time tonight to try and implement that, and see
> how it goes.
>
> Then I can start to think about how to write a macro and set up a data structure
> to instantiate arbitrarily selected patches, given the corner points. It's the
> lone corners and edges that might be tricky for me.
>...
Yes, be very careful with what you do at the corners and along the edges.
> Now, having better grasped what you were doing here, I'd say that based on my
> reading, this would give "G1 continuity".
Yes, that is also my understanding.
Here's more theory about this:
https://people.eecs.berkeley.edu/~sequin/CS284/LECT12/L4.html
> I think that my first time approaching this, I was trying to use 3x3 patches to
> give 4 control points and then do deCastejau to subdivide the super-pseudo
> Bezier spline suggested by those 4 points so that I could interpolate the inner
> control points of the edges in a "Bezier manner", if that makes sense.
When experimenting with these Bezier curves and patches I find it easier to use
Bernstein polynomials than to use de Castejau's algorithm.
>...
--
Tor Olav
http://subcube.com com> wrote:
>
> > I assume that you are looking at my 'Bezier_Patches_Stitched' files.
>
> Yes. They were, in fact, the motivation for my original attempts at stitching
> 9 patches together.
>...
=)
>...
> How did you smoothly connect the corner points in
> http://news.povray.org/web.5b7398619b869b61264be49d0%40news.povray.org ?
> Is that a bezier spline sphere-sweep?
> [Is it /beh-ZHEER/?]
Yes, that was done with sphere sweeps. As I have not found a Bezier type spline
in POV-Ray, I used linear_spline sphere_sweeps with many points placed along a
Bezier curve (that I calculated with some self made Bezier functions).
From your later posts in this thread it seems like you have now figured out how
to do something similar.
Anyway, for others that may be interested, I've attached an image which shows
which contol points to use for these "cubic Bezier sphere sweeps". I've colored
the relevant "sweeps" red and their control points green.
> I spent some time pondering the boundary conditions, and how to process 16
> patches like the stitched renders.
> What I've come up with is to
> create an array of 25 corner points
> create an array of 16 points, and "copy" the relevant corner points into the
> appropriate places
> calculate the linear vectors between the corners of each side
> set the control points on those sides to 1/3 and 2/3 of the vector
> Use those control points to interpolate the 4 inner control points in an
> analogous manner
I'm not sure if I follow you, but some of it sounds ok.
> I hope to get a little bit more time tonight to try and implement that, and see
> how it goes.
>
> Then I can start to think about how to write a macro and set up a data structure
> to instantiate arbitrarily selected patches, given the corner points. It's the
> lone corners and edges that might be tricky for me.
>...
Yes, be very careful with what you do at the corners and along the edges.
> Now, having better grasped what you were doing here, I'd say that based on my
> reading, this would give "G1 continuity".
Yes, that is also my understanding.
Here's more theory about this:
https://people.eecs.berkeley.edu/~sequin/CS284/LECT12/L4.html
> I think that my first time approaching this, I was trying to use 3x3 patches to
> give 4 control points and then do deCastejau to subdivide the super-pseudo
> Bezier spline suggested by those 4 points so that I could interpolate the inner
> control points of the edges in a "Bezier manner", if that makes sense.
When experimenting with these Bezier curves and patches I find it easier to use
Bernstein polynomials than to use de Castejau's algorithm.
>...
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'control_points_for_cubic_bezier_splines_along_edges_of_bicubic_bezier_patches.jp.jpg' (253 KB)
Preview of image 'control_points_for_cubic_bezier_splines_along_edges_of_bicubic_bezier_patches.jp.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> Given that a Bezier patch can be interpreted as a Bezier spline in one dimension
> whose control points slide along Bezier splines oriented in the other dimension,
> and that this can be expressed as a parametiric equation, then
>
> It ought to be possible to define a parametric {} object in POV-Ray based on a
> set of control points and the basis functions of the Bezier splines.
>...
Yes, that is possible. Just create 3 bivariate functions with the appropriate
Bernstein polynomials and feed them to the parametric object. But you need
patience for that...
> Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> the surface of the patch.
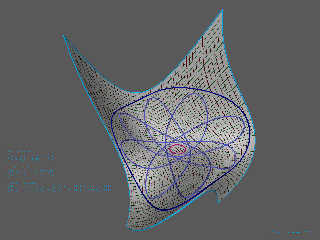
Yes, this image shows some white spheres and cylinders following a path in the
UV-space on the surface of a NURBS-patch:
http://dataduppedings.no/subcube/POV-Ray_Images/NURBS_Grid.jpg
See also the attached image where the I've put some sphere sweeps on a Bezier
patch. (Notice that you can read out the radii for the sphere swept curves
(0.06, 0.46 and 0.48) in the UV-mapped texture.)
>...
--
Tor Olav
http://subcube.com net> wrote:
>...
> Given that a Bezier patch can be interpreted as a Bezier spline in one dimension
> whose control points slide along Bezier splines oriented in the other dimension,
> and that this can be expressed as a parametiric equation, then
>
> It ought to be possible to define a parametric {} object in POV-Ray based on a
> set of control points and the basis functions of the Bezier splines.
>...
Yes, that is possible. Just create 3 bivariate functions with the appropriate
Bernstein polynomials and feed them to the parametric object. But you need
patience for that...
> Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> the surface of the patch.
Yes, this image shows some white spheres and cylinders following a path in the
UV-space on the surface of a NURBS-patch:
http://dataduppedings.no/subcube/POV-Ray_Images/NURBS_Grid.jpg
See also the attached image where the I've put some sphere sweeps on a Bezier
patch. (Notice that you can read out the radii for the sphere swept curves
(0.06, 0.46 and 0.48) in the UV-mapped texture.)
>...
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'sphere sweeps on a bicubic bezier patch.jpg' (333 KB)
Preview of image 'sphere sweeps on a bicubic bezier patch.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> Given that a Bezier patch can be interpreted as a Bezier spline in one dimension
> whose control points slide along Bezier splines oriented in the other dimension,
> and that this can be expressed as a parametiric equation, then
>
> It ought to be possible to define a parametric {} object in POV-Ray based on a
> set of control points and the basis functions of the Bezier splines.
>
> Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> the surface of the patch.
>
> This should also allow the generation of _any_ spline between the ordinate /
> cardinal splines defined by the corners. In theory one should be able to
> simulate a patch by juxtaposing a series of splines from one side to the other
> in either dimension.
If you calculate the two partial derivatives (d/dU and d/dV) for each of the
bivariate functions for a Bezier patch you can use these to reorient objects to
align with the U-, V- and normal directions of the surface.
This article contains some useful information about that:
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
The attached image shows cubes that are reoriented to align with the directions
I mentioned above. It also shows a lot of splines that creates a grid on the
surface of the patch.
>...
--
Tor Olav
http://subcube.com net> wrote:
>...
> Given that a Bezier patch can be interpreted as a Bezier spline in one dimension
> whose control points slide along Bezier splines oriented in the other dimension,
> and that this can be expressed as a parametiric equation, then
>
> It ought to be possible to define a parametric {} object in POV-Ray based on a
> set of control points and the basis functions of the Bezier splines.
>
> Then, given a point <m, n> (or <u, v>) on the surface, one could place things ON
> the surface of the patch.
>
> This should also allow the generation of _any_ spline between the ordinate /
> cardinal splines defined by the corners. In theory one should be able to
> simulate a patch by juxtaposing a series of splines from one side to the other
> in either dimension.
If you calculate the two partial derivatives (d/dU and d/dV) for each of the
bivariate functions for a Bezier patch you can use these to reorient objects to
align with the U-, V- and normal directions of the surface.
This article contains some useful information about that:
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
The attached image shows cubes that are reoriented to align with the directions
I mentioned above. It also shows a lot of splines that creates a grid on the
surface of the patch.
>...
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'cubes on the surface of a bicubic bezier patch.jpg' (432 KB)
Preview of image 'cubes on the surface of a bicubic bezier patch.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> "Bald Eagle" <cre### [at] netscape com> wrote:
> "Bald Eagle" <cre### [at] netscape net> wrote:
> >...
>...
> If you calculate the two partial derivatives (d/dU and d/dV) for each of the
> bivariate functions for a Bezier patch you can use these to reorient objects to
> align with the U-, V- and normal directions of the surface.
>
> This article contains some useful information about that:
>
>
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
>
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
Here's another image where the cubes have been scaled in the U/V-directions by
the lengths of the vectors used for reorienting them. (These vectors were
created with the partial derivatives of the bivariate functions for the Bezier
patch.)
--
Tor Olav
http://subcube.com net> wrote:
> >...
>...
> If you calculate the two partial derivatives (d/dU and d/dV) for each of the
> bivariate functions for a Bezier patch you can use these to reorient objects to
> align with the U-, V- and normal directions of the surface.
>
> This article contains some useful information about that:
>
>
https://www.scratchapixel.com/lessons/advanced-rendering/bezier-curve-rendering-utah-teapot/bezier-patch-normal
>
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
Here's another image where the cubes have been scaled in the U/V-directions by
the lengths of the vectors used for reorienting them. (These vectors were
created with the partial derivatives of the bivariate functions for the Bezier
patch.)
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'scaled_cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg' (426 KB)
Preview of image 'scaled_cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>...
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
I don't know why the preview of that image is not shown properly. (Perhaps the
height/width-dimensions are too big ?). Here's a try with smaller dimensions.
--
Tor Olav
http://subcube.com com> wrote:
>...
> The attached image shows cubes that are reoriented to align with the directions
> I mentioned above. It also shows a lot of splines that creates a grid on the
> surface of the patch.
I don't know why the preview of that image is not shown properly. (Perhaps the
height/width-dimensions are too big ?). Here's a try with smaller dimensions.
--
Tor Olav
http://subcube.com
Post a reply to this message
Attachments:
Download 'cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg' (172 KB)
Preview of image 'cubes_on_the_surface_of_a_bicubic_bezier_patch.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()