 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
The povray rotate command is so unintuitive, that I have been thinking
for many months about how to make things easier. I have made many
macros to make transformations easier for myself, but this one is
special. Instead of rotating around one axis at a time it rotates
around all three at once. My inspiration was an ordinary joystick.
Joystick input is a single rotation away from the starting point, but
internally it measures two rotations. My thought was why can't I do the
same thing in reverse. I find the new x axis from rotations around the
y, and z axis's. The new y, and z axis's are found in similar ways. I
create a matrix using the old, and new basis vectors. It tends to be
distorted, so it needs to be normalized. I didn't have a matrix
normalizing function, so i improvised by converting it to a quaternion,
witch is easy to normalize, and then converting it back. I think it
works well enough for rough work. The second major problem with it is
in special situations two or more axis's become the same, and the matrix
is degenerate. I think this can be overcome by doing something like
using the function twice with all of the angles cut in half. Maybe
someone who has actually taken a class in linear algebra, can figure it
out.
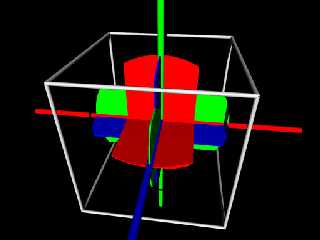
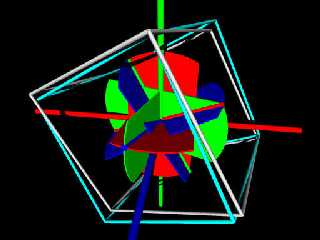
In the images the long Red, Green, and Blue cylinders are the x, y, and
z axis's. The short ones are the new ones after the rotation. The
white cylinders are the results of the matrix before normalizing. The
Cyan cylinders is the Matrix after normalizing. The first image is no
rotation, the third rotation has all angle double, the second image.
#macro Q_vlength(Q)
#local Q = Q*Q;
pow((Q.x + Q.y + Q.z + Q.t),.5)
#end
#macro Q_normalize(Q)
(Q/Q_vlength(Q))
#end
#macro Q_matrix (Q) // converts a quaternion into a matrix
#local Q0 = Q.x;
#local Q1 = Q.y;
#local Q2 = Q.z;
#local Q3 = Q.t;
#local QT = 2*pow(Q0,2)-1;
matrix
<QT+2*pow(Q1,2),2*(Q1*Q2+Q0*Q3),2*(Q1*Q3-Q0*Q2),
2*(Q1*Q2-Q0*Q3),QT+2*pow(Q2,2),2*(Q2*Q3+Q0*Q1),
2*(Q1*Q3+Q0*Q2),2*(Q2*Q3-Q0*Q1),QT+2*pow(Q3,2),
0,0,0>
#end
#macro Matrix_array_2_quaternion(Array)
#local M11 = Array[0];
#local M12 = Array[1];
#local M13 = Array[2];
#local M21 = Array[3];
#local M22 = Array[4];
#local M23 = Array[5];
#local M31 = Array[6];
#local M32 = Array[7];
#local M33 = Array[8];
#local Q0 = pow(M11+M22+M33+1,.5)/2;
#local Q04 = 4*Q0;
#local Q1 = (M23-M32)/Q04;
#local Q2 = (M31-M13)/Q04;
#local Q3 = (M12-M21)/Q04;
Q_normalize(<Q0,Q1,Q2,Q3>)
#end
#macro Symetric_rotations(V)
#local New_x = vcross(vrotate(y,z*V.z),vrotate(z,y*V.y));
#local New_y = vcross(vrotate(z,x*V.x),vrotate(x,z*V.z));
#local New_z = vcross(vrotate(x,y*V.y),vrotate(y,x*V.x));
#local Trans_ma = array[12] // create
cosine matrix, store in array
{vdot(x,New_x),vdot(y,New_x),vdot(z,New_x),
vdot(x,New_y),vdot(y,New_y),vdot(z,New_y),
vdot(x,New_z),vdot(y,New_z),vdot(z,New_z),0,0,0}
#local Trans_q = Matrix_array_2_quaternion(Trans_ma) // convert
to quaternion, and normalize
#local Trans_m = transform {Q_matrix(Trans_q)} // convert
from quaternion to rotation matrix
Trans_m
#end
--
Dan Johnson
http://www.geocities.com/zapob
Post a reply to this message
Attachments:
Download 'joystick1.jpg' (24 KB)
Download 'joystick2.jpg' (35 KB)
Download 'joystick3.jpg' (31 KB)
Preview of image 'joystick1.jpg'
Preview of image 'joystick2.jpg'

Preview of image 'joystick3.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Dan,
are you sure that your new basis vectors are
orthogonal to each other ?
If you insert some debug lines after the #local
declarations within your Symetric_rotations()
macro, you can check this. Like this:
#macro Symmetric_rotations(V)
#local New_x = vcross(vrotate(y, z*V.z), vrotate(z, y*V.y));
#local New_y = vcross(vrotate(z, x*V.x), vrotate(x, z*V.z));
#local New_z = vcross(vrotate(x, y*V.y), vrotate(y, x*V.x));
#debug "\n"
#debug str(vdot(New_x, New_y), 0, -1)
#debug "\n"
#debug str(vdot(New_x, New_z), 0, -1)
#debug "\n"
#debug str(vdot(New_y, New_z), 0, -1)
#debug "\n"
#local Trans_ma = array[12] {
vdot(x, New_x), vdot(y, New_x), vdot(z, New_x),
vdot(x, New_y), vdot(y, New_y), vdot(z, New_y),
vdot(x, New_z), vdot(y, New_z), vdot(z, New_z),
0, 0, 0
}
#local Trans_q = Matrix_array_2_quaternion(Trans_ma)
#local Trans_m = transform { Q_matrix(Trans_q) }
Trans_m
#end
I.e.: You should get three zeros every time.
(Let me know if you think that I'm wrong about this.)
Tor Olav
P.S.:
It's possible to do some simplifications to you macros ;)
- And I think that you don't even have to use quats.
When you have got yourself some orthogonal basis vectors,
then just normalize them in order to make them orthonormal.
And then try to use them directly within the matrix.
Dan Johnson wrote:
>
> The povray rotate command is so unintuitive, that I have been thinking
> for many months about how to make things easier. I have made many
> macros to make transformations easier for myself, but this one is
> special. Instead of rotating around one axis at a time it rotates
> around all three at once. My inspiration was an ordinary joystick.
> Joystick input is a single rotation away from the starting point, but
> internally it measures two rotations. My thought was why can't I do the
> same thing in reverse. I find the new x axis from rotations around the
> y, and z axis's. The new y, and z axis's are found in similar ways. I
> create a matrix using the old, and new basis vectors.
>...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Tor Olav Kristensen wrote:
>
> Dan,
>
> are you sure that your new basis vectors are
> orthogonal to each other ?
They aren't that's the primary problem
> I.e.: You should get three zeros every time.
> (Let me know if you think that I'm wrong about this.)
You are right. The idea was to create a skewed matrix, and then fix it
so that it is a rotation matrix, instead of a rotation, plus a bunch of
sheers and scales.
> Tor Olav
>
> P.S.:
> It's possible to do some simplifications to you macros ;)
>
> - And I think that you don't even have to use quats.
> When you have got yourself some orthogonal basis vectors,
> then just normalize them in order to make them orthonormal.
> And then try to use them directly within the matrix.
I know I don't have to use quats, but I don't know how to normalize a
matrix (remove the skew). All of the quaternion functions I used were
already in my library. It was a convenient way to get an idea of what
things would look like with a matrix algebra solution. The formula I
used for converting a matrix to a quaternion is only designed to work
with normalized rotation matrices, so I was pleased that my bad math
worked relatively close to what I was looking for.
--
Dan Johnson
http://www.geocities.com/zapob
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Dan Johnson wrote:
>
> Tor Olav Kristensen wrote:
> >
> > Dan,
> >
> > are you sure that your new basis vectors are
> > orthogonal to each other ?
>
> They aren't that's the primary problem
>
> > I.e.: You should get three zeros every time.
> > (Let me know if you think that I'm wrong about this.)
>
> You are right. The idea was to create a skewed matrix, and then fix it
> so that it is a rotation matrix, instead of a rotation, plus a bunch of
> sheers and scales.
>
> > Tor Olav
> >
> > P.S.:
> > It's possible to do some simplifications to you macros ;)
> >
> > - And I think that you don't even have to use quats.
> > When you have got yourself some orthogonal basis vectors,
> > then just normalize them in order to make them orthonormal.
> > And then try to use them directly within the matrix.
>
> I know I don't have to use quats, but I don't know how to normalize a
> matrix (remove the skew). All of the quaternion functions I used were
> already in my library. It was a convenient way to get an idea of what
> things would look like with a matrix algebra solution. The formula I
> used for converting a matrix to a quaternion is only designed to work
> with normalized rotation matrices, so I was pleased that my bad math
> worked relatively close to what I was looking for.
Sorry, I think that I misunderstood your problem.
Below is a macro you can try to use.
Tor Olav
#macro SymmRot(V)
#local NewX = vrotate(x, V);
#local NewY = vrotate(y, V);
#local NewZ = vrotate(z, V);
matrix <
NewX.x, NewX.y, NewX.z,
NewY.x, NewY.y, NewY.z,
NewZ.x, NewZ.y, NewZ.z,
0, 0, 0
>
#end // macro SymmRot
// And here's some code to verify it.
#declare vRot = <3, 7, 11>*3;
#declare MySphere =
sphere {
<0, 0, 0>, 0.01
scale <1, 100, 1>
translate 0.5*y
rotate <-11, -8, -7>*3
}
object {
MySphere
rotate vRot
pigment { color Yellow }
}
object {
MySphere
SymmRot(vRot)
pigment { color Cyan }
}
object {
MySphere
transform Symetric_rotations(vRot)
pigment { color Magenta }
}
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Tor Olav Kristensen wrote:
>
> Sorry, I think that I misunderstood your problem.
Most people don't understand me. Including myself.
Thanks for the input maybe I will try working more on it in a few
months. It was more of an interesting toy to begin with. When I am
serious about transforms I usually use a much more powerful transform
macro. H2t it by far the most used macro I have ever written(By me at
least). I think the code below will effectively demonstrate how ez it
makes things. Perfectly face bonded tetrahedra. If you keep using
Move1 you will get a tetrahelix.
#include "colors.inc"
light_source{ <-3,4,-5>*100 rgb 2}
camera{translate -8*z}
#macro H2tr(U1,U2,V1,V2) // Here to there rotation... two reference
points for initial and final positions
#local X1 = vnormalize(U1); // find basis vectors
of initial and
#local Z1 = vnormalize(vcross(X1,U2)); // final refrence
frames
#local Y1 = vcross(Z1,X1);
#local X2 = vnormalize(V1);
#local Z2 = vnormalize(vcross(X2,V2));
#local Y2 = vcross(Z2,X2);
#local Rotation = transform {
matrix <X1.x,Y1.x,Z1.x,X1.y,Y1.y,Z1.y,X1.z,Y1.z,Z1.z,0,0,0>
matrix
<vdot(X2,X1),vdot(X2,Y1),vdot(X2,Z1),vdot(Y2,X1),vdot(Y2,Y1),vdot(Y2,Z1),vdot(Z2,X1),vdot(Z2,Y1),vdot(Z2,Z1),0,0,0>
matrix <X1.x,X1.y,X1.z,Y1.x,Y1.y,Y1.z,Z1.x,Z1.y,Z1.z,0,0,0> }//
this is the transpose of the first matrix
Rotation
#end
#macro H2t (Oi,Ai,Ri,Of,Af,Rf) // Here to there
translate (- Oi) // center, and two reference
points on object
H2tr((Ai-Oi),(Ri-Oi),(Af-Of),(Rf-Of)) // New center, and
refrence point locations
translate Of
#end // (Origin, Absolute vector, Relative vector) initial, and final
orientations
#declare Tetrahedron = array[4]{<1,1,1>,<1,-1,-1>,<-1,1,-1>,<-1,-1,1>}
// Tetrahedron vertexes
#declare Tetrahedron_faces = mesh {
triangle { Tetrahedron[0], Tetrahedron[1], Tetrahedron[2]}
triangle { Tetrahedron[0], Tetrahedron[1], Tetrahedron[3]}
triangle { Tetrahedron[0], Tetrahedron[2], Tetrahedron[3]}
triangle { Tetrahedron[1], Tetrahedron[2], Tetrahedron[3]}
}
#declare Move1= transform
{H2t(<1,-1,-1>,<1,1,1>,<-1,-1,1>,<1,-1,-1>,<1,1,1>,<-1,1,-1>)}
object{Tetrahedron_faces pigment{Red}}
object{Tetrahedron_faces pigment{Green}transform{Move1}}
object{Tetrahedron_faces pigment{Blue}transform{Move1}transform{Move1}}
--
Dan Johnson
http://www.geocities.com/zapob
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Dan Johnson wrote:
>
> Tor Olav Kristensen wrote:
>
> >
> > Sorry, I think that I misunderstood your problem.
>
> Most people don't understand me. Including myself.
> Thanks for the input maybe I will try working more on it in a few
> months. It was more of an interesting toy to begin with. When I am
> serious about transforms I usually use a much more powerful transform
> macro. H2t it by far the most used macro I have ever written(By me at
> least). I think the code below will effectively demonstrate how ez it
> makes things. Perfectly face bonded tetrahedra. If you keep using
> Move1 you will get a tetrahelix.
>...
Dan, I had a second look at your code today.
And it took a while before I understood
what you were up to.
- It seems you have made a kind of
reorient macro, but with an added feature
to also control how a "local" coordinate
system within the object is repositioned.
Earlier I have been thinking along those
lines too. (And I think that John VanSickle
has made some similar macros.)
Now I have rewritten your "Here to there"
macros a little. (And I also introduced
some v3.5 features.)
Can you please have a look at these macros
to see if they still work as you intended ?
Tor Olav
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
// A common macro:
#macro MatrixFromVectors(vA, vB, vC)
matrix <
vA.x, vA.y, vA.z,
vB.x, vB.y, vB.z,
vC.x, vC.y, vC.z,
0, 0, 0
>
#end // macro macro MatrixFromVectors
// Former H2tr macro:
#macro Here2ThereTransform(vA1, vA2, vB1, vB2)
#local vX1 = vnormalize(vA1);
#local vZ1 = vnormalize(vcross(vX1, vA2));
#local vY1 = vcross(vZ1, vX1);
#local vX2 = vnormalize(vB1);
#local vZ2 = vnormalize(vcross(vX2, vB2));
#local vY2 = vcross(vZ2, vX2);
#local TransA = transform { MatrixFromVectors(vX1, vY1, vZ1) }
#local TransAinv = transform { TransA inverse }
#local Fn = function { transform { TransAinv } }
transform {
TransAinv
MatrixFromVectors(
Fn(vX2.x, vX2.y, vX2.z),
Fn(vY2.x, vY2.y, vY2.z),
Fn(vZ2.x, vZ2.y, vZ2.z)
)
TransA
}
#end // macro Here2ThereTransform
// Former H2t macro
#macro H2T_Transform(pCtrI, pRef1I, pRef2I, pCtrF, pRef1F, pRef2F)
transform {
translate -pCtrI
Here2ThereTransform(
pRef1I - pCtrI, pRef2I - pCtrI,
pRef1F - pCtrF, pRef2F - pCtrF
)
translate pCtrF
}
#end // macro H2T_Transform
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Tor Olav Kristensen wrote:
>...
> Dan, I had a second look at your code today.
>
> And it took a while before I understood
> what you were up to.
>
> - It seems you have made a kind of
> reorient macro, but with an added feature
> to also control how a "local" coordinate
> system within the object is repositioned.
>
> Earlier I have been thinking along those
> lines too. (And I think that John VanSickle
> has made some similar macros.)
>
> Now I have rewritten your "Here to there"
> macros a little. (And I also introduced
> some v3.5 features.)
>...
>...
> // Former H2tr macro:
> #macro Here2ThereTransform(vA1, vA2, vB1, vB2)
>
> #local vX1 = vnormalize(vA1);
> #local vZ1 = vnormalize(vcross(vX1, vA2));
> #local vY1 = vcross(vZ1, vX1);
> #local vX2 = vnormalize(vB1);
> #local vZ2 = vnormalize(vcross(vX2, vB2));
> #local vY2 = vcross(vZ2, vX2);
> #local TransA = transform { MatrixFromVectors(vX1, vY1, vZ1) }
> #local TransAinv = transform { TransA inverse }
> #local Fn = function { transform { TransAinv } }
>
> transform {
> TransAinv
> MatrixFromVectors(
> Fn(vX2.x, vX2.y, vX2.z),
> Fn(vY2.x, vY2.y, vY2.z),
> Fn(vZ2.x, vZ2.y, vZ2.z)
> )
> TransA
> }
>
> #end // macro Here2ThereTransform
>...
I just returned from a little trip to North
Norway today. - And while sitting on the airport
bus I convinced myself that the Here2ThereTransform()
macro I posted can be simplified further to this:
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
#macro Here2ThereTransform(vA1, vA2, vB1, vB2)
#local vX1 = vnormalize(vA1);
#local vZ1 = vnormalize(vcross(vX1, vA2));
#local vY1 = vcross(vZ1, vX1);
#local vX2 = vnormalize(vB1);
#local vZ2 = vnormalize(vcross(vX2, vB2));
#local vY2 = vcross(vZ2, vX2);
#local TA = transform { MatrixFromVectors(vX1, vY1, vZ1) inverse }
#local TB = transform { MatrixFromVectors(vX2, vY2, vZ2) }
transform { TA TB }
#end // macro Here2ThereTransform
// ===== 1 ======= 2 ======= 3 ======= 4 ======= 5 ======= 6 ======= 7
I've just done some simple tests and it seems
to work ok.
Tor Olav
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()