The povray rotate command is so unintuitive, that I have been thinking
for many months about how to make things easier.  I have made many
macros to make transformations easier for myself, but this one is
special.  Instead of rotating around one axis at a time it rotates
around all three at once.  My inspiration was an ordinary joystick. 
Joystick input is a single rotation away from the starting point, but
internally it measures two rotations.  My thought was why can't I do the
same thing in reverse.  I find the new x axis from rotations around the
y, and z axis's.  The new y, and z axis's are found in similar ways.  I
create a matrix using the old, and new basis vectors.  It tends to be
distorted, so it needs to be normalized.  I didn't have a matrix
normalizing function, so i improvised by converting it to a quaternion,
witch is easy to normalize, and then converting it back.  I think it
works well enough for rough work.  The second major problem with it is
in special situations two or more axis's become the same, and the matrix
is degenerate.  I think this can be overcome by doing something like
using the function twice with all of the angles cut in half.  Maybe
someone who has actually taken a class in linear algebra, can figure it
out.  

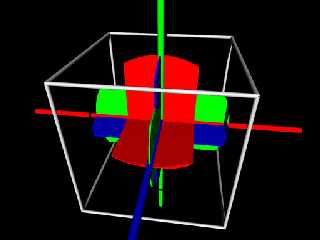
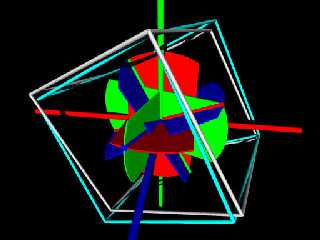
In the images the long Red, Green, and Blue cylinders are the x, y, and
z axis's.  The short ones are the new ones after the rotation.  The
white cylinders are the results of the matrix before normalizing.  The
Cyan cylinders is the Matrix after normalizing.  The first image is no
rotation, the third rotation has all angle double, the second image.  

#macro Q_vlength(Q)
        #local Q = Q*Q;
        pow((Q.x + Q.y + Q.z + Q.t),.5)
#end
#macro Q_normalize(Q)
        (Q/Q_vlength(Q))
#end
#macro Q_matrix (Q)      // converts a quaternion into a matrix
        #local Q0 = Q.x;
        #local Q1 = Q.y;
        #local Q2 = Q.z;
        #local Q3 = Q.t;
        #local QT = 2*pow(Q0,2)-1;
        matrix 
        <QT+2*pow(Q1,2),2*(Q1*Q2+Q0*Q3),2*(Q1*Q3-Q0*Q2),
         2*(Q1*Q2-Q0*Q3),QT+2*pow(Q2,2),2*(Q2*Q3+Q0*Q1),
         2*(Q1*Q3+Q0*Q2),2*(Q2*Q3-Q0*Q1),QT+2*pow(Q3,2),
         0,0,0>
#end
#macro Matrix_array_2_quaternion(Array)
        #local M11 = Array[0];
        #local M12 = Array[1];
        #local M13 = Array[2];
        #local M21 = Array[3];
        #local M22 = Array[4];
        #local M23 = Array[5];
        #local M31 = Array[6];
        #local M32 = Array[7];
        #local M33 = Array[8];
        
        #local Q0 = pow(M11+M22+M33+1,.5)/2;
        #local Q04 = 4*Q0;
        #local Q1 = (M23-M32)/Q04;
        #local Q2 = (M31-M13)/Q04;
        #local Q3 = (M12-M21)/Q04;
        
        Q_normalize(<Q0,Q1,Q2,Q3>)
#end

#macro Symetric_rotations(V)
        #local New_x = vcross(vrotate(y,z*V.z),vrotate(z,y*V.y));
        #local New_y = vcross(vrotate(z,x*V.x),vrotate(x,z*V.z));
        #local New_z = vcross(vrotate(x,y*V.y),vrotate(y,x*V.x));
        
        #local Trans_ma = array[12]                           // create
cosine matrix, store in array
                {vdot(x,New_x),vdot(y,New_x),vdot(z,New_x),
                 vdot(x,New_y),vdot(y,New_y),vdot(z,New_y),
                 vdot(x,New_z),vdot(y,New_z),vdot(z,New_z),0,0,0}
        #local Trans_q = Matrix_array_2_quaternion(Trans_ma)  // convert
to quaternion, and normalize
        #local Trans_m = transform {Q_matrix(Trans_q)}        // convert
from quaternion to rotation matrix
        
        Trans_m
#end

-- 
Dan Johnson 

http://www.geocities.com/zapob

Post a reply to this message

Attachments:
Download 'joystick1.jpg' (24 KB) Download 'joystick2.jpg' (35 KB) Download 'joystick3.jpg' (31 KB)

Preview of image 'joystick1.jpg'

Preview of image 'joystick2.jpg'

Preview of image 'joystick3.jpg'