 |
 |
|
 |
|
 |
|  |
|  |
|
 |
From: William F Pokorny
Subject: Suggest v4.0 f_kappa_2d() function. (yuqk R19 v0.6.13.0)
Date: 23 Feb 2025 08:43:28
Message: <67bb2600$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
Adding the inbuilt f_kappa_2d() function to the upcoming release (R19)
of yuqk).
This a general helper function / technique to match any two curves at
their endpoints given you have the means to calculate the first and
second derivatives for both curves being glued together at (t).
The function will calculate and return 'k(t)' or the 'radius of
curvature' (1.0/k(t)).
Attaching images showing on the left k(t), and on the right the 'radius
of curvature' at t, as the length of the normal vectors for a
f_bezier_2d_cubic() curve.
Bill P.
Post a reply to this message
Attachments:
Download 'f_bezier_2d_cubickappaplay.png' (66 KB)
Preview of image 'f_bezier_2d_cubickappaplay.png'
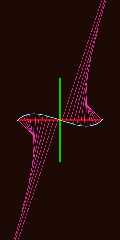
|
 |
|  |
|  |
|
 |
From: William F Pokorny
Subject: Re: Suggest v4.0 f_kappa_2d() function. (yuqk R19 v0.6.13.0)
Date: 23 Feb 2025 08:51:05
Message: <67bb27c9$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 2/23/25 08:43, William F Pokorny wrote:
> Attaching images showing on the left k(t), and on the right the 'radius
> of curvature' at t
Dang. Posted the wrong image... Correct one attached.
Bill P.
Post a reply to this message
Attachments:
Download 'f_kappa_2dstory.png' (119 KB)
Preview of image 'f_kappa_2dstory.png'
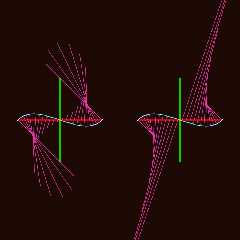
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> This a general helper function / technique to match any two curves at
> their endpoints given you have the means to calculate the first and
> second derivatives for both curves being glued together at (t).
Are f' and f" arguments to the function?
> The function will calculate and return 'k(t)' or the 'radius of
> curvature' (1.0/k(t)).
>
> Attaching images showing on the left k(t), and on the right the 'radius
> of curvature' at t, as the length of the normal vectors for a
> f_bezier_2d_cubic() curve.
That's pretty slick.
(If you add f'", then you can match RATE of curvature, so that reflections are
smooth as well.)
Do you plug f_bezier_2d_cubic() into your function and it calculates the
derivatives? Can you plug in, say, Perlin Noise, and have that work?
You've been busy! :)
- BW org> wrote:
> This a general helper function / technique to match any two curves at
> their endpoints given you have the means to calculate the first and
> second derivatives for both curves being glued together at (t).
Are f' and f" arguments to the function?
> The function will calculate and return 'k(t)' or the 'radius of
> curvature' (1.0/k(t)).
>
> Attaching images showing on the left k(t), and on the right the 'radius
> of curvature' at t, as the length of the normal vectors for a
> f_bezier_2d_cubic() curve.
That's pretty slick.
(If you add f'", then you can match RATE of curvature, so that reflections are
smooth as well.)
Do you plug f_bezier_2d_cubic() into your function and it calculates the
derivatives? Can you plug in, say, Perlin Noise, and have that work?
You've been busy! :)
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: Alain Martel
Subject: Re: Suggest v4.0 f_kappa_2d() function. (yuqk R19 v0.6.13.0)
Date: 23 Feb 2025 10:32:54
Message: <67bb3fa6$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
Le 2025-02-23 à 09:07, Bald Eagle a écrit :
> William F Pokorny <ano### [at] anonymous org> wrote:
>
>> This a general helper function / technique to match any two curves at
>> their endpoints given you have the means to calculate the first and
>> second derivatives for both curves being glued together at (t).
>
> Are f' and f" arguments to the function?
>
>> The function will calculate and return 'k(t)' or the 'radius of
>> curvature' (1.0/k(t)).
>>
>> Attaching images showing on the left k(t), and on the right the 'radius
>> of curvature' at t, as the length of the normal vectors for a
>> f_bezier_2d_cubic() curve.
>
> That's pretty slick.
> (If you add f'", then you can match RATE of curvature, so that reflections are
> smooth as well.)
>
>
> Do you plug f_bezier_2d_cubic() into your function and it calculates the
> derivatives? Can you plug in, say, Perlin Noise, and have that work?
>
> You've been busy! :)
>
> - BW
>
f' and f" being first and second derivatives, it's easy to calculate
them on the fly.
Let say that you have f(x) = 7x^2+-3x+6,
then, f'(x) = 7x-3,
and f"(x) = 7 org> wrote:
>
>> This a general helper function / technique to match any two curves at
>> their endpoints given you have the means to calculate the first and
>> second derivatives for both curves being glued together at (t).
>
> Are f' and f" arguments to the function?
>
>> The function will calculate and return 'k(t)' or the 'radius of
>> curvature' (1.0/k(t)).
>>
>> Attaching images showing on the left k(t), and on the right the 'radius
>> of curvature' at t, as the length of the normal vectors for a
>> f_bezier_2d_cubic() curve.
>
> That's pretty slick.
> (If you add f'", then you can match RATE of curvature, so that reflections are
> smooth as well.)
>
>
> Do you plug f_bezier_2d_cubic() into your function and it calculates the
> derivatives? Can you plug in, say, Perlin Noise, and have that work?
>
> You've been busy! :)
>
> - BW
>
f' and f" being first and second derivatives, it's easy to calculate
them on the fly.
Let say that you have f(x) = 7x^2+-3x+6,
then, f'(x) = 7x-3,
and f"(x) = 7
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: William F Pokorny
Subject: Re: Suggest v4.0 f_kappa_2d() function. (yuqk R19 v0.6.13.0)
Date: 23 Feb 2025 16:00:48
Message: <67bb8c80$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 2/23/25 09:07, Bald Eagle wrote:
> William F Pokorny <ano### [at] anonymous org> wrote:
>
>> This a general helper function / technique to match any two curves at
>> their endpoints given you have the means to calculate the first and
>> second derivatives for both curves being glued together at (t).
>
> Are f' and f" arguments to the function?
Could be, but see below.
>
>> The function will calculate and return 'k(t)' or the 'radius of
>> curvature' (1.0/k(t)).
>>
>> Attaching images showing on the left k(t), and on the right the 'radius
>> of curvature' at t, as the length of the normal vectors for a
>> f_bezier_2d_cubic() curve.
>
...
>
> Do you plug f_bezier_2d_cubic() into your function and it calculates the
> derivatives? Can you plug in, say, Perlin Noise, and have that work?
>
Sort of.
No. The capability isn't that general - and limited to 2D (*).
With the f_bezier_2d_* functions and, for example, f_catenary() from a
few releases back, the function which generates the curve has too
calculation modes inbuilt for the first and second derivatives - and
sometimes the third as well.
So the typical set up would be something like:
//...
#declare FnBez_2d = function (ro_t,ro_mode) {
f_bezier_2d_cubic(
f_enc2x_f32(-1.0,0),
f_enc2x_f32(-1/2,0.5),
f_enc2x_f32(+1/2,-0.5),
f_enc2x_f32(1.0,0),
ro_t,ro_mode
)
}
#declare U02 = union {
#for (I,0,SphCnt,4)
...
#declare D1 = FnBez_2d(I/SphCnt,3); // Calc raw 1st derivative
#declare D2 = FnBez_2d(I/SphCnt,4); // Calc raw 2nd derivative
#declare Kappa = f_kappa_2d(D1,D2,0); // Pass the values
...
#end
texture { pigment { Frostbite } finish {emission 1.0} }
}
//...
Where you have a univariate polynomial for the curve, it's not too bad
to calculate the derivative polynomials as Alain pointed out.
Bill P.
(*) Lying some as by measuring local deltas we could probably come up
with D1 & D2 values which would be in the ballpark to some sampling
accuracy. org> wrote:
>
>> This a general helper function / technique to match any two curves at
>> their endpoints given you have the means to calculate the first and
>> second derivatives for both curves being glued together at (t).
>
> Are f' and f" arguments to the function?
Could be, but see below.
>
>> The function will calculate and return 'k(t)' or the 'radius of
>> curvature' (1.0/k(t)).
>>
>> Attaching images showing on the left k(t), and on the right the 'radius
>> of curvature' at t, as the length of the normal vectors for a
>> f_bezier_2d_cubic() curve.
>
...
>
> Do you plug f_bezier_2d_cubic() into your function and it calculates the
> derivatives? Can you plug in, say, Perlin Noise, and have that work?
>
Sort of.
No. The capability isn't that general - and limited to 2D (*).
With the f_bezier_2d_* functions and, for example, f_catenary() from a
few releases back, the function which generates the curve has too
calculation modes inbuilt for the first and second derivatives - and
sometimes the third as well.
So the typical set up would be something like:
//...
#declare FnBez_2d = function (ro_t,ro_mode) {
f_bezier_2d_cubic(
f_enc2x_f32(-1.0,0),
f_enc2x_f32(-1/2,0.5),
f_enc2x_f32(+1/2,-0.5),
f_enc2x_f32(1.0,0),
ro_t,ro_mode
)
}
#declare U02 = union {
#for (I,0,SphCnt,4)
...
#declare D1 = FnBez_2d(I/SphCnt,3); // Calc raw 1st derivative
#declare D2 = FnBez_2d(I/SphCnt,4); // Calc raw 2nd derivative
#declare Kappa = f_kappa_2d(D1,D2,0); // Pass the values
...
#end
texture { pigment { Frostbite } finish {emission 1.0} }
}
//...
Where you have a univariate polynomial for the curve, it's not too bad
to calculate the derivative polynomials as Alain pointed out.
Bill P.
(*) Lying some as by measuring local deltas we could probably come up
with D1 & D2 values which would be in the ballpark to some sampling
accuracy.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()