Hi,

Francois LE COAT writes:
>> Here is a part of Mandelbrot fractal set in 3D with my software:
>>

>>
>> In Eureka 2.12 the function is julia(x-0.1562+i*(y+1.0323),0)

>> of distances algorithm. The function julia(z,z') corresponds to
>> the Mandelbrot set when z varies, and Julia when z' varies.
>>
>> Here is a part of Julia fractal subset in 3D with my software:
>>

>>
>> In Eureka 2.12 the function is julia(-0.82+i*0.18,y*exp(i*x))
>> plotted in [-PI/2,PI/2][0,PI/2] The 3D is obtained with the
>> approximation of distances algorithm. The function julia(z,z')
>> corresponds to the Mandelbrot set when z varies, and Julia when
>> z' varies.
>>
>> The surfaces were exported from Eureka 2.12 in 3D ".TRI" format and
>> transformed into a POV-Ray script with `tri2pov.ttp`. The same move
>> around the surface is performed, with rotations of one degree. This
>> is an illustration of the export possibilities of Eureka 2.12 =)
>>
>> I wish you will appreciate...
> 
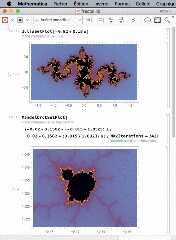
> Here is corresponding Julia and Mandelbrot fractal sets with
> Mathematica software, in the attached "fractal.gif" picture.
> 
> The Mandelbrot set is the same, except the colormap. But for
> the Julia subset, I draw julia(-0.82+i*0.18,y*exp(i*x)) with
> my software, and Mathematica draws julia(-0.82+i*0.18,x+i*y).
> 
> I don't know if there is this kind of transform in Mathematica?
> 
> Maybe someone of you all, can help?...
> 
> Merry Christmas.

Here is a video from Julia subset drawn with my Eureka 2.12 soft:

	<https://www.youtube.com/watch?v=uA20AhHiKc4>

It is using the ARAnyM GNU/GPL ATARI virtual machine under macOS.

Happy New Year.

Best regards,

-- 

Author of Eureka 2.12 (2D Graph Describer, 3D Modeller)
http://eureka.atari.org/

Post a reply to this message

Attachments:
Download 'fractal.gif' (100 KB)

Preview of image 'fractal.gif'