I assure you that I suffered a code injection while there was a "prove that you
are not a robot" loop.
A loop that evidently affects only Chrome, and predisposes it to receive false
aggressive notifications every time you open Chrome. However, I managed to block
them via Chrome's site blocking.
I could see the original page for half a second, then it was injected with spam.
Now I saw the includes you posted.
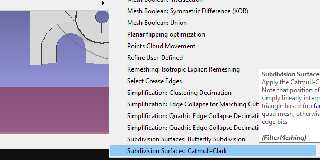
It is a known algorithm, I already have it, with other algorithms, on MeshLab
(see shot).
With MeshLab the transformation can be done on the 3D file. It is persistent.
The includes only do it for the PovRay render.
I need persistent, because I use the same files for 3D printing. So I thank you
but the "static" transformation method is preferable because the 3D file (povray
or STL or CAD) is already complete. Launched on PovRay it consumes infinitely
less memory. Too bad there is no example file in the zip, to see the results on
complex shapes, it also seems very complicated to implement it on each mesh of a
job.
He only shows the shot of a small job, but not how he passes the original
polygonal data to the includes.

Post a reply to this message

Attachments:
Download 'clipboard01.png' (29 KB)

Preview of image 'clipboard01.png'

but let's go back to the interesting observation that jr made
Too few polygons in some places (it was a car signal light) are not nice
You're right, I thought about it.

General algorithms are no good in my opinion.
They are recursive and have unintelligent ways.
They consume memory.
They exaggerate in the points that are already rich and perhaps are deficient in
the points that need it most.

I thought of a different criterion, to be applied only on "poor" polygons.
It is not easy but not impossible to write.
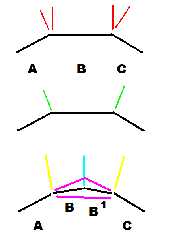
I attach the scheme of my idea.
I have 3 quads (seen from above).

I select the central one B, to improve it by splitting it in two.

Above, the 3 black quads with their normals red.
In the center, their green vertex normals, computed for POVray's smooth
triangles.


Below, I've broken B into two parts, B and B1. Finding the split point as the
midpoint between its original midline and the intersection of its lateral quads.


Now I have to recalculate the new normals ...
blue and yellow.
The bad quad is gone. If it's not enough I can select another bad quad.
Here I simplified, the sides are symmetrical, but it's just to simplify the
drawing. You can always do it.

When I have two free hours to concentrate I try.

Post a reply to this message

Attachments:
Download 'clipboard01.png' (6 KB)

Preview of image 'clipboard01.png'