 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"GioSeregni" <gms### [at] hotmail com> wrote:
> "jr" <cre### [at] gmail com> wrote:
> "jr" <cre### [at] gmail com> wrote:
> > hi,
> >
> > "GioSeregni" <gms### [at] hotmail com> wrote:
> > hi,
> >
> > "GioSeregni" <gms### [at] hotmail com> wrote:
> > > For an excellent result the code must have at least 3 steps
> > > 1) (already done), calculation of the average of the normals affecting the
> > > point.
> > > 2) Correcting the weight of the normals per point if they also come from
> > > triangles with a large surface area
> > > 3) Corrective of the normals if the adjacent triangles have an inclination
> > > between them that tends to approach 90 degrees
> >
> > fwiw, my 'gts2pov' takes triangle area into account when calculating the
> > normals. also just found mention of a 'stl2pov' software :
> > <https://news.povray.org/web.6156c51533af95845bd1b3ba6cde94f1%40news.povray.org>
> >
> > <https://wiki.povray.org/content/User:Jr>
> >
> >
> > regards, jr.
>
> Tx JR!
> My code is already working from STL to POV even with the color subset of STL.
> In fact I have to add the surface calculation to the loops from triangle to
> smooth_triangle, I'll take a look at your system. But first I also want to
> translate the color, as I already do with the triangles, dividing groups of
> differently colored meshes. This way my translator will also become faster
> because the loops are compact and short on small meshes.
> (between different colors I don't want smooth).
> In the center STL, on the left the current smooth routine, on the right the
> simple triangle mesh. Thank you!
I May be wrong but I don't believe the normals length will be taken into account
at all. I believe they are rather always 'normalized' (no pun) to a value of 1
and just their directions used. Some of the most valuable input may be from
Alain with all his technical POV knowledge. the only things that then would
change the apparent curvature of normals *globally* is the 'brilliance' keyword
value or more locally the slope normal pattern... but again all this needs to be
verified. com> wrote:
> > > For an excellent result the code must have at least 3 steps
> > > 1) (already done), calculation of the average of the normals affecting the
> > > point.
> > > 2) Correcting the weight of the normals per point if they also come from
> > > triangles with a large surface area
> > > 3) Corrective of the normals if the adjacent triangles have an inclination
> > > between them that tends to approach 90 degrees
> >
> > fwiw, my 'gts2pov' takes triangle area into account when calculating the
> > normals. also just found mention of a 'stl2pov' software :
> > <https://news.povray.org/web.6156c51533af95845bd1b3ba6cde94f1%40news.povray.org>
> >
> > <https://wiki.povray.org/content/User:Jr>
> >
> >
> > regards, jr.
>
> Tx JR!
> My code is already working from STL to POV even with the color subset of STL.
> In fact I have to add the surface calculation to the loops from triangle to
> smooth_triangle, I'll take a look at your system. But first I also want to
> translate the color, as I already do with the triangles, dividing groups of
> differently colored meshes. This way my translator will also become faster
> because the loops are compact and short on small meshes.
> (between different colors I don't want smooth).
> In the center STL, on the left the current smooth routine, on the right the
> simple triangle mesh. Thank you!
I May be wrong but I don't believe the normals length will be taken into account
at all. I believe they are rather always 'normalized' (no pun) to a value of 1
and just their directions used. Some of the most valuable input may be from
Alain with all his technical POV knowledge. the only things that then would
change the apparent curvature of normals *globally* is the 'brilliance' keyword
value or more locally the slope normal pattern... but again all this needs to be
verified.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
"GioSeregni" <gms### [at] hotmail com> wrote:
> ...
> Tx JR!
welcome. a visual to compare, the mesh is from the GTS home site.
<https://news.povray.org/web.610401e9687fa6155e0fed26cde94f1%40news.povray.org>
> My code is already working from STL to POV even with the color subset of STL.
ah, colour is something I ought to look into, too. cheers.
regards, jr. com> wrote:
> ...
> Tx JR!
welcome. a visual to compare, the mesh is from the GTS home site.
<https://news.povray.org/web.610401e9687fa6155e0fed26cde94f1%40news.povray.org>
> My code is already working from STL to POV even with the color subset of STL.
ah, colour is something I ought to look into, too. cheers.
regards, jr.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I tried a search of the NG to see what else there might be, these were the only
2 so far to catch my eye.
Maybe some small thing in there might trigger an idea, yet untested.
Warp:
https://news.povray.org/3cd536d5%40news.povray.org
jceddy:
http://news.povray.org/povray.general/thread/%3Cweb.442a6fe16260549766ffc7a50@news.povray.org%3E/
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> I tried a search of the NG to see what else there might be, these were the only
> 2 so far to catch my eye.
>
> Maybe some small thing in there might trigger an idea, yet untested.
>
> Warp:
> https://news.povray.org/3cd536d5%40news.povray.org
>
> jceddy:
>
http://news.povray.org/povray.general/thread/%3Cweb.442a6fe16260549766ffc7a50@news.povray.org%3E/
>
> - BW
Tx Jr and BW for the links, I use exactly the average..
warning about colors in STL
They aren't true color
I use this code by STL (subset of colors) to POV (truecolor)
r=STLface.descriptor AND 31744
r=r SHR 10
r=r*8
g=STLface.descriptor AND 992
g=g SHR 5
g=g*8
b=STLface.descriptor AND 31
b=b*8
POV_COLOR=b+(g*256)+(r*65536)
NOTE: this is my struct for STL's face
TYPE STL
header As String * 80
numfacets As Long '4 b then -> loop
nx As Single '4 b
ny As Single
nz As Single
x0 As Single
y0 AS Single
z0 As Single
x1 As Single
y1 As Single
z1 As Single
x2 As Single
y2 As Single
z2 As Single
descriptor As Short '2 b <--- end loop
END TYPE
DIM STLface AS STL net> wrote:
> I tried a search of the NG to see what else there might be, these were the only
> 2 so far to catch my eye.
>
> Maybe some small thing in there might trigger an idea, yet untested.
>
> Warp:
> https://news.povray.org/3cd536d5%40news.povray.org
>
> jceddy:
>
http://news.povray.org/povray.general/thread/%3Cweb.442a6fe16260549766ffc7a50@news.povray.org%3E/
>
> - BW
Tx Jr and BW for the links, I use exactly the average..
warning about colors in STL
They aren't true color
I use this code by STL (subset of colors) to POV (truecolor)
r=STLface.descriptor AND 31744
r=r SHR 10
r=r*8
g=STLface.descriptor AND 992
g=g SHR 5
g=g*8
b=STLface.descriptor AND 31
b=b*8
POV_COLOR=b+(g*256)+(r*65536)
NOTE: this is my struct for STL's face
TYPE STL
header As String * 80
numfacets As Long '4 b then -> loop
nx As Single '4 b
ny As Single
nz As Single
x0 As Single
y0 AS Single
z0 As Single
x1 As Single
y1 As Single
z1 As Single
x2 As Single
y2 As Single
z2 As Single
descriptor As Short '2 b <--- end loop
END TYPE
DIM STLface AS STL
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"GioSeregni" <gms### [at] hotmail com> wrote:
> Hi all, first I apologize for my bad english.
> I finished now developing (basic version no color at this moment) a small
> transformation tool from STL mesh, in the center, to mesh with smooth_triangles.
Hello Giovanni!
Your results are already looking very good! :-) Congratulations for figuring out
this kind of translation. (I have been busy working on the 'opposite'
translation-- POV-ray objects to STL.)
A little utility called 'stl2pov' was mentioned. I remember it from years ago.
It is still available here, although it apparently runs in Python(?). It might
give you some ideas and suggestions about your problem.
https://github.com/rsmith-nl/stltools
By the way, I also thought that the normals of triangles are direction vectors
of 'unit length' by default, not smaller or larger, but I could be wrong.
I am looking forward to seeing how you solve your too-smooth problem; I wish
that I could offer some suggestions. Some of this triangle stuff is outside my
knowledge. *If* the triangle normals are all unit length, perhaps your summing
operation could be made to eliminate some of the identical normals on large flat
areas, which might reduce their contribution-- and make the smoothness less
smooth. (?) com> wrote:
> Hi all, first I apologize for my bad english.
> I finished now developing (basic version no color at this moment) a small
> transformation tool from STL mesh, in the center, to mesh with smooth_triangles.
Hello Giovanni!
Your results are already looking very good! :-) Congratulations for figuring out
this kind of translation. (I have been busy working on the 'opposite'
translation-- POV-ray objects to STL.)
A little utility called 'stl2pov' was mentioned. I remember it from years ago.
It is still available here, although it apparently runs in Python(?). It might
give you some ideas and suggestions about your problem.
https://github.com/rsmith-nl/stltools
By the way, I also thought that the normals of triangles are direction vectors
of 'unit length' by default, not smaller or larger, but I could be wrong.
I am looking forward to seeing how you solve your too-smooth problem; I wish
that I could offer some suggestions. Some of this triangle stuff is outside my
knowledge. *If* the triangle normals are all unit length, perhaps your summing
operation could be made to eliminate some of the identical normals on large flat
areas, which might reduce their contribution-- and make the smoothness less
smooth. (?)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Kenneth" <kdw### [at] gmail com> wrote:
*If* the triangle normals are all unit length, perhaps your summing
> operation could be made to eliminate some of the identical normals on large flat
> areas, which might reduce their contribution-- and make the smoothness less
> smooth. (?)
or maybe... MORE smooth? So perhaps the normals on LARGER triangles could be
*duplicated* in your summing process instead, to make their contribution have
more weight, resulting in a *less*-smooth result. Based on the size or computed
area of each triangle.
I apologize for just guessing about this, because I don't fully understand all
of the details of your idea. com> wrote:
*If* the triangle normals are all unit length, perhaps your summing
> operation could be made to eliminate some of the identical normals on large flat
> areas, which might reduce their contribution-- and make the smoothness less
> smooth. (?)
or maybe... MORE smooth? So perhaps the normals on LARGER triangles could be
*duplicated* in your summing process instead, to make their contribution have
more weight, resulting in a *less*-smooth result. Based on the size or computed
area of each triangle.
I apologize for just guessing about this, because I don't fully understand all
of the details of your idea.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Kenneth" <kdw### [at] gmail com> wrote:
> I am looking forward to seeing how you solve your too-smooth problem; I wish
> that I could offer some suggestions. Some of this triangle stuff is outside my
> knowledge. *If* the triangle normals are all unit length, perhaps your summing
> operation could be made to eliminate some of the identical normals on large flat
> areas, which might reduce their contribution-- and make the smoothness less
> smooth. (?)
Triangles typically have a sinlge normal - a vector that is perpendicular to
it's face (in either direction).
The normal can be of any length.
Typically, for lighting purposes, since the normal vector is used to calculate
how light interacts with the surface, you want them of unit length.
For smooth, or perturbed-surfaces, you will specify the normals of the vertices,
and then POV-Ray will interpolate the normals across the surface, (and perhaps
adding/multiplying by some pattern) to yield a smoothly changing surface.
When dealing with a mesh of triangles that share common vertices and edges, one
typically averages all of the normals that meet at a common vertex so that
there's no sudden discontinuity in the way light reflects from the surface,
appearing as lump, depressions, or creases.
If you have two triangles oriented in different directions, if you multiply the
length of the normal of one triangle, its contribution to how the triangles
behave at that vertex will be greater.
I think in order to accomplish what he's looking to do, the way that the
triangles get interpolated would have to change, other wise I don't see how to
maintain a common normal direction on one end, and non-linearly change apparent
curvature at the other.
It's not something I've played with in detail, but it sure seems like something
that ought to be explored with test renders, diagrams, normal directions and
lengths explicitly labeled, etc.
Good instructional articles are what draw computer graphics students and
hobbyists to any given site for the quality content.
We should have that.
Right on the home page. Perhaps directing to a specific (new) sub-group titled
"Articles".
- BW com> wrote:
> I am looking forward to seeing how you solve your too-smooth problem; I wish
> that I could offer some suggestions. Some of this triangle stuff is outside my
> knowledge. *If* the triangle normals are all unit length, perhaps your summing
> operation could be made to eliminate some of the identical normals on large flat
> areas, which might reduce their contribution-- and make the smoothness less
> smooth. (?)
Triangles typically have a sinlge normal - a vector that is perpendicular to
it's face (in either direction).
The normal can be of any length.
Typically, for lighting purposes, since the normal vector is used to calculate
how light interacts with the surface, you want them of unit length.
For smooth, or perturbed-surfaces, you will specify the normals of the vertices,
and then POV-Ray will interpolate the normals across the surface, (and perhaps
adding/multiplying by some pattern) to yield a smoothly changing surface.
When dealing with a mesh of triangles that share common vertices and edges, one
typically averages all of the normals that meet at a common vertex so that
there's no sudden discontinuity in the way light reflects from the surface,
appearing as lump, depressions, or creases.
If you have two triangles oriented in different directions, if you multiply the
length of the normal of one triangle, its contribution to how the triangles
behave at that vertex will be greater.
I think in order to accomplish what he's looking to do, the way that the
triangles get interpolated would have to change, other wise I don't see how to
maintain a common normal direction on one end, and non-linearly change apparent
curvature at the other.
It's not something I've played with in detail, but it sure seems like something
that ought to be explored with test renders, diagrams, normal directions and
lengths explicitly labeled, etc.
Good instructional articles are what draw computer graphics students and
hobbyists to any given site for the quality content.
We should have that.
Right on the home page. Perhaps directing to a specific (new) sub-group titled
"Articles".
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> "Kenneth" <kdw### [at] gmail net> wrote:
> "Kenneth" <kdw### [at] gmail com> wrote:
>
> > I am looking forward to seeing how you solve your too-smooth problem; I wish
> > that I could offer some suggestions. Some of this triangle stuff is outside my
> > knowledge. *If* the triangle normals are all unit length, perhaps your summing
> > operation could be made to eliminate some of the identical normals on large flat
> > areas, which might reduce their contribution-- and make the smoothness less
> > smooth. (?)
>
> Triangles typically have a sinlge normal - a vector that is perpendicular to
> it's face (in either direction).
>
> The normal can be of any length.
>
> Typically, for lighting purposes, since the normal vector is used to calculate
> how light interacts with the surface, you want them of unit length.
>
> For smooth, or perturbed-surfaces, you will specify the normals of the vertices,
> and then POV-Ray will interpolate the normals across the surface, (and perhaps
> adding/multiplying by some pattern) to yield a smoothly changing surface.
>
> When dealing with a mesh of triangles that share common vertices and edges, one
> typically averages all of the normals that meet at a common vertex so that
> there's no sudden discontinuity in the way light reflects from the surface,
> appearing as lump, depressions, or creases.
>
> If you have two triangles oriented in different directions, if you multiply the
> length of the normal of one triangle, its contribution to how the triangles
> behave at that vertex will be greater.
>
> I think in order to accomplish what he's looking to do, the way that the
> triangles get interpolated would have to change, other wise I don't see how to
> maintain a common normal direction on one end, and non-linearly change apparent
> curvature at the other.
>
> It's not something I've played with in detail, but it sure seems like something
> that ought to be explored with test renders, diagrams, normal directions and
> lengths explicitly labeled, etc.
>
> Good instructional articles are what draw computer graphics students and
> hobbyists to any given site for the quality content.
>
> We should have that.
> Right on the home page. Perhaps directing to a specific (new) sub-group titled
> "Articles".
>
> - BW
tx Bw
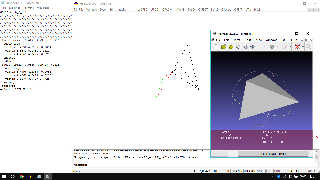
I am working around this concept. The bad angle is 90 degrees. The vectors are
ever long 1 (red color), so the distance (green) it's approximately 1,4142
(Pitagora).
Around this value I have to eliminate the smoothing. It involves graduating on
the size of the angles. Unfortunately I don't have much training in
trigonometry... it takes me a long time and I don't know the shortcuts in the
formulas, I need time...
TX Again
G. com> wrote:
>
> > I am looking forward to seeing how you solve your too-smooth problem; I wish
> > that I could offer some suggestions. Some of this triangle stuff is outside my
> > knowledge. *If* the triangle normals are all unit length, perhaps your summing
> > operation could be made to eliminate some of the identical normals on large flat
> > areas, which might reduce their contribution-- and make the smoothness less
> > smooth. (?)
>
> Triangles typically have a sinlge normal - a vector that is perpendicular to
> it's face (in either direction).
>
> The normal can be of any length.
>
> Typically, for lighting purposes, since the normal vector is used to calculate
> how light interacts with the surface, you want them of unit length.
>
> For smooth, or perturbed-surfaces, you will specify the normals of the vertices,
> and then POV-Ray will interpolate the normals across the surface, (and perhaps
> adding/multiplying by some pattern) to yield a smoothly changing surface.
>
> When dealing with a mesh of triangles that share common vertices and edges, one
> typically averages all of the normals that meet at a common vertex so that
> there's no sudden discontinuity in the way light reflects from the surface,
> appearing as lump, depressions, or creases.
>
> If you have two triangles oriented in different directions, if you multiply the
> length of the normal of one triangle, its contribution to how the triangles
> behave at that vertex will be greater.
>
> I think in order to accomplish what he's looking to do, the way that the
> triangles get interpolated would have to change, other wise I don't see how to
> maintain a common normal direction on one end, and non-linearly change apparent
> curvature at the other.
>
> It's not something I've played with in detail, but it sure seems like something
> that ought to be explored with test renders, diagrams, normal directions and
> lengths explicitly labeled, etc.
>
> Good instructional articles are what draw computer graphics students and
> hobbyists to any given site for the quality content.
>
> We should have that.
> Right on the home page. Perhaps directing to a specific (new) sub-group titled
> "Articles".
>
> - BW
tx Bw
I am working around this concept. The bad angle is 90 degrees. The vectors are
ever long 1 (red color), so the distance (green) it's approximately 1,4142
(Pitagora).
Around this value I have to eliminate the smoothing. It involves graduating on
the size of the angles. Unfortunately I don't have much training in
trigonometry... it takes me a long time and I don't know the shortcuts in the
formulas, I need time...
TX Again
G.
Post a reply to this message
Attachments:
Download 'clipboard01.jpg' (476 KB)
Preview of image 'clipboard01.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
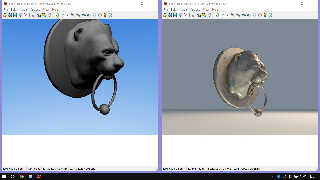
There was an interesting comment with a utility to download, but now I don't see
it anymore. Has it been cancelled? I took the obj and converted it to STL then
applied my code to it, but without refinements in the environment. I tested his
example with my program, because I had downloaded it, my render is poor.. it has
no texture, it has no lights... I put the linked example but rendered with my
version 3.7 (the file was 3.8 ) Strange, I can no longer find who posted and the
content, thanks anyway!
Post a reply to this message
Attachments:
Download 'clip.jpg' (399 KB)
Preview of image 'clip.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> "Kenneth" <kdw### [at] gmail net> wrote:
> "Kenneth" <kdw### [at] gmail com> wrote:
>
> > I am looking forward to seeing how you solve your too-smooth problem; I wish
> > that I could offer some suggestions. Some of this triangle stuff is outside my
> > knowledge. *If* the triangle normals are all unit length, perhaps your summing
> > operation could be made to eliminate some of the identical normals on large flat
> > areas, which might reduce their contribution-- and make the smoothness less
> > smooth. (?)
>
> Triangles typically have a sinlge normal - a vector that is perpendicular to
> it's face (in either direction).
>
> The normal can be of any length.
>
> Typically, for lighting purposes, since the normal vector is used to calculate
> how light interacts with the surface, you want them of unit length.
>
> For smooth, or perturbed-surfaces, you will specify the normals of the vertices,
> and then POV-Ray will interpolate the normals across the surface, (and perhaps
> adding/multiplying by some pattern) to yield a smoothly changing surface.
>
> When dealing with a mesh of triangles that share common vertices and edges, one
> typically averages all of the normals that meet at a common vertex so that
> there's no sudden discontinuity in the way light reflects from the surface,
> appearing as lump, depressions, or creases.
>
> If you have two triangles oriented in different directions, if you multiply the
> length of the normal of one triangle, its contribution to how the triangles
> behave at that vertex will be greater.
>
> I think in order to accomplish what he's looking to do, the way that the
> triangles get interpolated would have to change, other wise I don't see how to
> maintain a common normal direction on one end, and non-linearly change apparent
> curvature at the other.
>
> It's not something I've played with in detail, but it sure seems like something
> that ought to be explored with test renders, diagrams, normal directions and
> lengths explicitly labeled, etc.
>
> Good instructional articles are what draw computer graphics students and
> hobbyists to any given site for the quality content.
>
> We should have that.
> Right on the home page. Perhaps directing to a specific (new) sub-group titled
> "Articles".
Hi Bill
Here's two relevant articles:
"Weighted Vertex Normals"
http://www.bytehazard.com/articles/vertnorm.html
"On the computation of vertex normals"
http://meshlabstuff.blogspot.com/2009/04/on-computation-of-vertex-normals.html
- And then there's this paper, which delves deep into the topic:
"A comparison of algorithms for vertex normal computation"
Shuangshuang Jin, Robert R. Lewis, David West
The Visual Computer, 2005 - Springer
Vertex normal algorithms investigated in that article:
Mean edge weighted by cotangents of subtended angles
Mean weighted by angle
Mean weighted by areas of adjacent triangles
Mean weighted equally
Mean weighted by edge length reciprocals
Mean weighted by square root of edge length reciprocals
Mean weighted by sine and edge length reciprocals
From the article's "Conclusions and future work":
Relatively speaking, except for trigonometrically parameterized surfaces,
"Mean weighted by angle" is most frequently a good choice. If speed is a
concern, however, "Mean weighted equally" holds up well in most cases.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
>
> > I am looking forward to seeing how you solve your too-smooth problem; I wish
> > that I could offer some suggestions. Some of this triangle stuff is outside my
> > knowledge. *If* the triangle normals are all unit length, perhaps your summing
> > operation could be made to eliminate some of the identical normals on large flat
> > areas, which might reduce their contribution-- and make the smoothness less
> > smooth. (?)
>
> Triangles typically have a sinlge normal - a vector that is perpendicular to
> it's face (in either direction).
>
> The normal can be of any length.
>
> Typically, for lighting purposes, since the normal vector is used to calculate
> how light interacts with the surface, you want them of unit length.
>
> For smooth, or perturbed-surfaces, you will specify the normals of the vertices,
> and then POV-Ray will interpolate the normals across the surface, (and perhaps
> adding/multiplying by some pattern) to yield a smoothly changing surface.
>
> When dealing with a mesh of triangles that share common vertices and edges, one
> typically averages all of the normals that meet at a common vertex so that
> there's no sudden discontinuity in the way light reflects from the surface,
> appearing as lump, depressions, or creases.
>
> If you have two triangles oriented in different directions, if you multiply the
> length of the normal of one triangle, its contribution to how the triangles
> behave at that vertex will be greater.
>
> I think in order to accomplish what he's looking to do, the way that the
> triangles get interpolated would have to change, other wise I don't see how to
> maintain a common normal direction on one end, and non-linearly change apparent
> curvature at the other.
>
> It's not something I've played with in detail, but it sure seems like something
> that ought to be explored with test renders, diagrams, normal directions and
> lengths explicitly labeled, etc.
>
> Good instructional articles are what draw computer graphics students and
> hobbyists to any given site for the quality content.
>
> We should have that.
> Right on the home page. Perhaps directing to a specific (new) sub-group titled
> "Articles".
Hi Bill
Here's two relevant articles:
"Weighted Vertex Normals"
http://www.bytehazard.com/articles/vertnorm.html
"On the computation of vertex normals"
http://meshlabstuff.blogspot.com/2009/04/on-computation-of-vertex-normals.html
- And then there's this paper, which delves deep into the topic:
"A comparison of algorithms for vertex normal computation"
Shuangshuang Jin, Robert R. Lewis, David West
The Visual Computer, 2005 - Springer
Vertex normal algorithms investigated in that article:
Mean edge weighted by cotangents of subtended angles
Mean weighted by angle
Mean weighted by areas of adjacent triangles
Mean weighted equally
Mean weighted by edge length reciprocals
Mean weighted by square root of edge length reciprocals
Mean weighted by sine and edge length reciprocals
From the article's "Conclusions and future work":
Relatively speaking, except for trigonometrically parameterized surfaces,
"Mean weighted by angle" is most frequently a good choice. If speed is a
concern, however, "Mean weighted equally" holds up well in most cases.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()