|
 |
vase:
There are a few things that occurred to me, inspiring a few ideas to explore and
either confirm or refute their merit.
1. Given that there is all of this "sacred geometry" stuff that people go on
about, what is it's origin and why?
I think that we are taking a look at objects and structures that are designed
using a method much like we use CAD, however I think we can agree that the
ancients didn't have computers as we know them, and they probably used an
absolute measurement system different than our own.
But what makes absolute units irrelevant, and simultaneously preserves the
constants that we see?
Relative measurements. In geometry class, everything is laid out with a compass
and straightedge, and nothing is measured in "units". But everything is
measured in relation to line segment lengths, radii, etc.
The Greeks apparently got a lot of their knowledge from the Egyptians, and so
this comports with what we (think we) know about history.
2. If the designers used a well-developed system to lay out the design
parameters of objects and structures, and it was a relative system, then it
seems likely that they made use of all of the methods used in standard geometry.
Things would be laid out using arcs and lines and ratios. Pi would naturally
show up everywhere because ... circles.
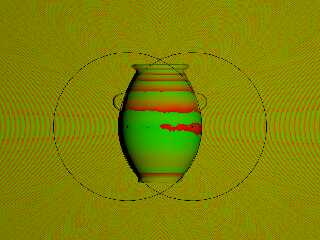
3. Alex Dunn and Nick Sierra used a sphere in their metrological analysis - not
because they were trying to show that a sphere in any way "matched" the surface
of the vase, but more to show that the distance of the surface to the ideal
sphere was very constant along the vertical axis (among other reasons).
You showed that the overall vase shape deviates from an ellipsoid with your
overlay.
It occurred to me that if I was going to build a machine with a tooling guide
that was inspired by classical geometrical methods, then I'd use a lot of
circular arcs. Which led me to think that the vase might more strongly resemble
a vesica piscis, or when the circle centers do not lie on the the other circle,
what is called a geometrical lemon. This is also exactly the inner surface of a
spindle torus.
I've spent a lot of time developing some macros for use in fitting circles and
spheres to measured data sets, and coming up with a way to compare the vase to
the lemon shape. Fortunately, POV-Ray has some inbuilt functions and primitives
that ultimately make that task a lot simpler, and I was able to devise a 3D
texturing pattern that is essentially an unsigned distance function of the
lemon. By applying this pattern to the vase mesh, it maps the closeness of fit
of the mesh to the lemon.
The result is obviously sensitive to the radii of the generating torus, as well
as the vertical positioning of the pattern. I used the data from your recent
Twitter post to estimate the arc of the side of the vase, and using the chord
length and depth of that putative circle segment, calculated the radius of the
required circle. I used the vertical height of the maximal external radius of
the vase, since that made the most sense, in terms of the machining operation.
(I'm going to try to use the data points from scanning the vase to fit a circle
using the least-squares stuff, and see what happens with that)
****
And here's what's interesting: The curvature/shape of the vase seems to be
reasonably consistent with that below the handles, and only deviates above that.
Of course, that's as far as a tool traveling along a fixed arc could make it
before beginning to machine away the torus that would eventually give rise to
the handles. Also, the only significant deviation from that curvature is right
along the centerline of the two circles.
Owning a lathe myself, this would typically be the area that an operator is most
likely to accidentally come in contact with, either with a tool, the tool
support, or some other fixture or tool being moved in close proximity to the
spinning work.
4. I think it might be a prudent change of tactics to think about how the vase
would have been machined - the order of operations, and see if that inspires any
new ideas and areas of investigation.
Post a reply to this message
Attachments:
Download 'vaselemoncomparison.png' (1167 KB)
Preview of image 'vaselemoncomparison.png'
|
 |




![]()